Contents
- A Brief History of Perceptrons
- Multilayer Perceptrons
- Just Show Me the Code
- FootNotes
- Further Reading
A Brief History of Perceptrons
The perceptron, that neural network whose name evokes how the future looked from the perspective of the 1950s, is a simple algorithm intended to perform binary classification; i.e. it predicts whether input belongs to a certain category of interest or not: fraud or not_fraudcat or not_cat.
Das Perzeptron nimmt in der Geschichte der neuronalen Netze und der künstlichen Intelligenz einen besonderen Platz ein, denn der anfängliche Hype um seine Leistung führte zu einer Widerlegung durch Minsky und Papert und zu einer weit verbreiteten Gegenreaktion, die die Forschung an neuronalen Netzen jahrzehntelang in den Hintergrund drängte – ein Winter der neuronalen Netze, der erst mit der Forschung von Geoff Hinton in den 2000er Jahren gänzlich aufgetaut wurde und dessen Ergebnisse seither die Gemeinschaft des maschinellen Lernens überrollt haben.
Frank Rosenblatt, der Pate des Perzeptrons, machte es als Gerät und nicht als Algorithmus bekannt. Das Perzeptron kam zunächst als Hardware auf den Markt.1 Rosenblatt, ein Psychologe, der an der Cornell University studierte und später Vorlesungen hielt, erhielt vom U.S. Office of Naval Research finanzielle Unterstützung für den Bau einer lernfähigen Maschine. Seine Maschine, das Mark I Perceptron, sah wie folgt aus.

Ein Perceptron ist ein linearer Klassifikator, d.h. ein Algorithmus, der Eingaben klassifiziert, indem er zwei Kategorien durch eine gerade Linie trennt. Die Eingabe ist typischerweise ein Merkmalsvektor x, der mit Gewichten w multipliziert und zu einem Bias b addiert wird: y = w * x + b.
Ein Perzeptron erzeugt eine einzelne Ausgabe auf der Grundlage mehrerer reellwertiger Eingaben, indem es eine lineare Kombination unter Verwendung seiner Eingabegewichte bildet (und die Ausgabe manchmal durch eine nichtlineare Aktivierungsfunktion leitet). So kann man das in Mathematik ausdrücken:
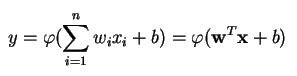
wobei w den Vektor der Gewichte, x den Vektor der Eingaben, b die Vorspannung und phi die nichtlineare Aktivierungsfunktion bezeichnet.
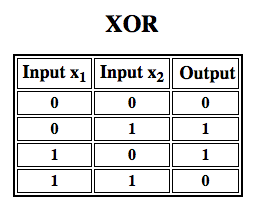
Rosenblatt baute ein einschichtiges Perzeptron. Das heißt, sein Hardware-Algorithmus enthielt keine mehreren Schichten, die es neuronalen Netzen ermöglichen, eine Merkmalshierarchie zu modellieren. Es handelte sich also um ein flaches neuronales Netz, was sein Perzeptron daran hinderte, nichtlineare Klassifizierungen durchzuführen, wie z. B. die XOR-Funktion (ein XOR-Operator wird ausgelöst, wenn die Eingabe entweder das eine oder das andere Merkmal aufweist, aber nicht beide; er steht für „exklusives ODER“), wie Minsky und Papert in ihrem Buch gezeigt haben.
Wenden Sie Reinforcement Learning auf Simulationen an“
Multilayer Perceptrons (MLP)
Nachfolgende Arbeiten mit mehrschichtigen Perceptrons haben gezeigt, dass diese in der Lage sind, einen XOR-Operator sowie viele andere nicht-lineare Funktionen zu approximieren.
Genauso wie Rosenblatt das Perzeptron auf ein 1943 entwickeltes McCulloch-Pitts-Neuron aufbaute, sind auch die Perzeptrons selbst Bausteine, die sich erst in so großen Funktionen wie den mehrschichtigen Perzeptrons als nützlich erweisen.2)
Das mehrschichtige Perzeptron ist die Hallo-Welt des Deep Learning: ein guter Ausgangspunkt, wenn man etwas über Deep Learning lernen will.
Ein mehrschichtiges Perzeptron (MLP) ist ein tiefes, künstliches neuronales Netzwerk. Es besteht aus mehr als einem Perceptron. Sie bestehen aus einer Eingabeschicht, die das Signal empfängt, einer Ausgabeschicht, die eine Entscheidung oder Vorhersage über die Eingabe trifft, und einer beliebigen Anzahl versteckter Schichten dazwischen, die den eigentlichen Rechenmotor des MLP darstellen. MLPs mit einer versteckten Schicht sind in der Lage, jede kontinuierliche Funktion zu approximieren.
Multilayer Perceptrons werden häufig bei überwachten Lernproblemen3 eingesetzt: Sie trainieren mit einer Reihe von Eingabe-Ausgabe-Paaren und lernen, die Korrelation (oder Abhängigkeiten) zwischen diesen Eingaben und Ausgaben zu modellieren. Beim Training werden die Parameter, d. h. die Gewichte und Verzerrungen, des Modells angepasst, um den Fehler zu minimieren. Backpropagation wird verwendet, um diese Anpassungen der Gewichte und Verzerrungen im Verhältnis zum Fehler vorzunehmen, und der Fehler selbst kann auf verschiedene Weise gemessen werden, u. a. durch den mittleren quadratischen Fehler (Root Mean Squared Error, RMSE).
Feedforward-Netzwerke wie MLPs sind wie Tennis oder Ping Pong. Sie sind hauptsächlich an zwei Bewegungen beteiligt, einem ständigen Hin und Her. Man kann sich dieses Pingpong von Vermutungen und Antworten als eine Art beschleunigte Wissenschaft vorstellen, denn jede Vermutung ist ein Test dessen, was wir zu wissen glauben, und jede Antwort ist eine Rückmeldung, die uns zeigt, wie falsch wir liegen.
Im Vorwärtsdurchlauf bewegt sich der Signalfluss von der Eingabeschicht durch die verborgenen Schichten zur Ausgabeschicht, und die Entscheidung der Ausgabeschicht wird an den Grundwahrheitsbezeichnungen gemessen.
Im Rückwärtsdurchlauf werden mit Hilfe von Backpropagation und der Kettenregel der Infinitesimalrechnung partielle Ableitungen der Fehlerfunktion in Bezug auf die verschiedenen Gewichte und Vorspannungen durch die MLP zurückverfolgt. Durch diese Differenzierung erhält man einen Gradienten oder eine Fehlerlandschaft, entlang derer die Parameter angepasst werden können, um die MLP einen Schritt näher an das Fehlerminimum zu bringen. Dies kann mit jedem gradientenbasierten Optimierungsalgorithmus wie dem stochastischen Gradientenabstieg geschehen. Das Netz spielt dieses Tennisspiel so lange, bis der Fehler nicht mehr kleiner werden kann. Dieser Zustand wird als Konvergenz bezeichnet.
Fußnoten
1) Interessant ist hier, dass Software und Hardware auf einem Flussdiagramm existieren: Software kann als Hardware ausgedrückt werden und umgekehrt. Wenn Chips wie FPGAs programmiert oder ASICs konstruiert werden, um einen bestimmten Algorithmus in Silizium zu backen, implementieren wir einfach Software eine Ebene tiefer, damit sie schneller funktioniert. Ebenso kann das, was in Silizium eingebrannt oder mit Lichtern und Potentiometern verdrahtet ist, wie Rosenblatts Mark I, auch symbolisch in Code ausgedrückt werden. Deshalb hat Alan Kay gesagt: „Wer sich wirklich ernsthaft mit Software befasst, sollte seine eigene Hardware herstellen“. Aber es gibt kein kostenloses Mittagessen, d.h. was man an Geschwindigkeit gewinnt, wenn man Algorithmen in Silizium einbaut, verliert man an Flexibilität und umgekehrt. Dies ist ein echtes Problem beim maschinellen Lernen, da sich die Algorithmen durch den Kontakt mit Daten verändern. Die Herausforderung besteht darin, die Teile des Algorithmus zu finden, die stabil bleiben, auch wenn sich die Parameter ändern; z. B. die linearen Algebra-Operationen, die derzeit von GPUs am schnellsten verarbeitet werden.
2) Ihre Gedanken könnten sich auf den nächsten Schritt hin zu immer komplexeren und auch nützlicheren Algorithmen richten. Wir bewegen uns von einem Neuron zu mehreren, genannt Schicht; wir bewegen uns von einer Schicht zu mehreren, genannt mehrschichtiges Perceptron. Können wir von einem MLP zu mehreren übergehen oder setzen wir einfach immer mehr Schichten ein, wie es Microsoft mit seinem ImageNet-Gewinner ResNet getan hat, das mehr als 150 Schichten hatte? Oder ist die richtige Kombination von MLPs ein Ensemble aus vielen Algorithmen, die in einer Art rechnerischer Demokratie über die beste Vorhersage abstimmen? Oder handelt es sich um die Einbettung eines Algorithmus in einen anderen, wie wir es bei graphischen Faltungsnetzen tun?
3) Sie werden bei Google, dem wahrscheinlich fortschrittlichsten KI-Unternehmen der Welt, in großem Umfang für eine Vielzahl von Aufgaben eingesetzt, obwohl es komplexere Methoden auf dem neuesten Stand der Technik gibt.
Further Reading
- Das Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, Cornell Aeronautical Laboratory, Psychological Review, von Frank Rosenblatt, 1958 (PDF)
- A Logical Calculus of Ideas Immanent in Nervous Activity, W. S. McCulloch & Walter Pitts, 1943
- Perceptrons: An Introduction to Computational Geometry, von Marvin Minsky & Seymour Papert
- Multi-Layer Perceptrons (MLP)
- Hebbian Theory
Andere Pathmind Wiki Posts
- Deep Neural Networks
- Recurrent Neural Networks (RNNs) and LSTMs
- Word2vec and Neural Word Embeddings
- Convolutional Neural Networks (CNNs) and Image Processing
- Accuracy, Precision and Recall
- Attention Mechanisms and Transformers
- Eigenvectors, Eigenvalues, PCA, Covariance and Entropy
- Graph Analytics and Deep Learning
- Symbolic Reasoning and Machine Learning
- Markov Chain Monte Carlo, AI and Markov Blankets
- Deep Reinforcement Learning
- Generative Adversarial Networks (GANs)
- AI vs Machine Learning vs Deep Learning