Zurück zum Lektionsindex | Lektionen der Reihe nach bearbeiten | Druckfreundliche Seite
Der Faktorsatz
Der Faktorsatz ist ein Ergebnis des Restgittersatzes und beruht auf denselben Überlegungen. Wenn Sie die Lektion über den Restsatz noch nicht gelesen haben, sollten Sie dieses Thema zuerst durcharbeiten und dann hierher zurückkehren.
Wie der Restsatz zeigt, erhält man einen Nullrest, wenn man ein Polynom p(x) durch einen Faktor x – a dieses Polynoms teilt. Betrachten wir noch einmal den Ausdruck des Divisionsalgorithmus für das Polynom:
Anzeige
- (x) = (x – a)q(x) + r(x)
Wenn x – a tatsächlich ein Faktor von p(x) ist, dann ist der Rest nach der Division durch x – a gleich Null. Das heißt:
p(x) = (x – a)q(x)
In Bezug auf den Restsatz bedeutet dies, dass, wenn x – a ein Faktor von p(x) ist, der Rest bei der synthetischen Division durch
x = a gleich Null ist.
Der Punkt des Faktorsatzes ist die Umkehrung des Restsatzes: Wenn man ein Polynom synthetisch durch x = a dividiert und einen Rest von Null erhält, dann ist nicht nur x = a eine Nullstelle des Polynoms (dank des Remainder Theorem), sondern x – a ist auch ein Faktor des Polynoms (dank des Factor Theorem).
Genauso wie beim Remainder Theorem geht es hier nicht darum, die lange Division eines gegebenen Polynoms durch einen gegebenen Faktor durchzuführen. Dieser Satz wiederholt nicht, was Sie bereits wissen, sondern versucht, Ihnen das Leben einfacher zu machen. Bei einer Übung mit dem Faktorsatz wendest du die synthetische Division an und überprüfst dann, ob der Rest Null ist.
- Bestimme mithilfe des Faktorsatzes, ob x – 1 ein Faktor von
f (x) = 2×4 + 3×2 – 5x + 7 ist.
Damit x – 1 ein Faktor von f (x) = 2×4 + 3×2 – 5x + 7 ist, muss x = 1 eine Nullstelle von f (x) sein. Um zu prüfen, ob x – 1 ein Faktor ist, setze ich zunächst x – 1 gleich Null und löse, um die vorgeschlagene Nullstelle, x = 1, zu finden. Dann benutze ich die synthetische Division, um f (x) durch x = 1 zu teilen. Da es keinen kubischen Term gibt, werde ich darauf achten, dass ich in die erste Zeile der synthetischen Division eine „0“ einfüge, um die weggelassene Potenz von x in 2×4 + 3×2 – 5x + 7 darzustellen:
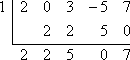
Da der Rest nicht Null ist, besagt der Faktorsatz, dass:
x – 1 kein Faktor von f (x) ist.
- Überprüfen Sie mit Hilfe des Faktorsatzes, dass x + 4 ein Faktor von
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16 ist.
Wenn x + 4 ein Faktor ist, dann ist (wenn man diesen Faktor gleich Null setzt und löst) x = -4 eine Wurzel. Um die geforderte Überprüfung durchzuführen, muss ich prüfen, dass ich bei der synthetischen Division von f (x) mit x = -4 einen Rest von Null erhalte:
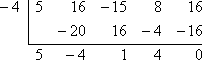
Der Rest ist Null, also besagt der Faktorsatz:
x + 4 ist ein Faktor von 5×4 + 16×3 – 15×2 + 8x + 16.
In der Praxis wird der Faktorsatz verwendet, wenn man Polynome „vollständig“ faktorisiert. Anstatt verschiedene Faktoren mit Hilfe der langen Division zu suchen, verwendet man die synthetische Division und den Faktorsatz. Jedes Mal, wenn Sie durch eine Zahl (die eine potenzielle Wurzel des Polynoms ist) dividieren und bei der synthetischen Division einen Rest von Null erhalten, bedeutet dies, dass die Zahl tatsächlich eine Wurzel ist, und somit ist „x minus die Zahl“ ein Faktor. Dann fährst du mit der Division des resultierenden kleineren Polynoms fort, bis du einen linearen Faktor (also alle Faktoren gefunden hast) oder einen quadratischen (auf den du die quadratische Formel anwenden kannst) erhältst.
- Nutze die Tatsache, dass -2 und 1/3 die Nullstellen von f (x) = 3×4 + 5×3 + x2 + 5x – 2 sind, und faktorisiere das Polynom vollständig. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
Wenn x = -2 eine Nullstelle ist, dann ist x + 2 = 0, also ist x + 2 ein Faktor. Ähnlich ist es, wenn x = 1/3 eine Null ist, dann ist x – 1/3 = 0, also ist x – 1/3 ein Faktor. Indem sie mir zwei der Nullen gegeben haben, haben sie mir auch zwei Faktoren gegeben: x + 2 und x – 1/3.
Da ich von einem Polynom vierten Grades ausgegangen bin, bleibt nach der Division der beiden gegebenen Faktoren eine Quadratform übrig. Dieses Quadrat kann ich mit der Quadratischen Formel oder einer anderen Methode lösen.
Der Faktorsatz besagt, dass ich die lange Division mit den bekannten Faktoren von x + 2 und x – 1/3 nicht durchführen muss. Stattdessen kann ich die synthetische Division mit den zugehörigen Nullen -2 und 1/3 verwenden. So sieht es aus, wenn ich die erste Division mit x = -2 durchführe:
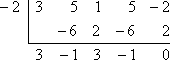
Der Rest ist Null, was zu erwarten ist, weil man mir zu Beginn gesagt hatte, dass -2 eine bekannte Nullstelle des Polynoms ist. Anstatt noch einmal mit dem ursprünglichen Polynom zu beginnen, werde ich nun mit dem verbleibenden Polynomfaktor von 3×3 – x2 + 3x – 1 (aus der unteren Zeile der synthetischen Division) arbeiten. Ich werde dies durch die andere gegebene Nullstelle, x = 1/3, teilen:
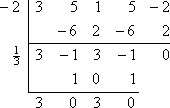
Damit habe ich die quadratische Gleichung 3×2 + 3, die ich lösen kann:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Wenn die Nullstellen x = -i und x = i sind, dann sind die Faktoren x – (-i) und x – (i), oder x + i und x – i. I need to remember that I divided off a „3“ when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. „The Factor Theorem.“ Purplemath. Available from 2016
|