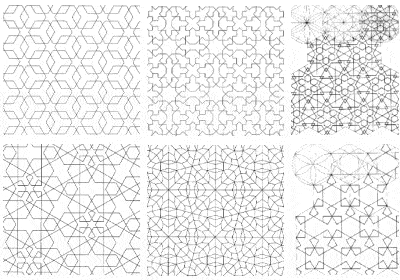
Einige Beispiele für die komplexen Symmetrien, die in der islamischen Tempeldekoration verwendet wurden
Das islamische Reich, das sich ab dem 8. Jahrhundert über Persien, den Nahen Osten, Zentralasien, Nordafrika, Iberien und Teile Indiens erstreckte, leistete bedeutende Beiträge zur Mathematik. Jahrhundert in Persien, dem Nahen Osten, Zentralasien, Afrika und auf der iberischen Halbinsel sowie in Teilen Indiens etabliert hatte, leistete einen bedeutenden Beitrag zur Mathematik. Sie konnten auf die mathematischen Entwicklungen Griechenlands und Indiens zurückgreifen und sie miteinander verschmelzen.
Eine Folge des islamischen Verbots, die menschliche Gestalt abzubilden, war die umfassende Verwendung komplexer geometrischer Muster zur Dekoration ihrer Gebäude, wodurch die Mathematik zu einer Kunst erhoben wurde. Tatsächlich entdeckten muslimische Künstler im Laufe der Zeit alle verschiedenen Formen der Symmetrie, die auf einer zweidimensionalen Fläche dargestellt werden können.
Der Koran selbst ermutigte zur Anhäufung von Wissen, und ein Goldenes Zeitalter der islamischen Wissenschaft und Mathematik blühte während der gesamten mittelalterlichen Periode vom 9. bis 15. Das Haus der Weisheit wurde um 810 in Bagdad gegründet, und fast sofort wurde mit der Übersetzung der wichtigsten griechischen und indischen mathematischen und astronomischen Werke ins Arabische begonnen.
Der herausragende persische Mathematiker Muhammad Al-Khwarizmi war ein früher Direktor des Hauses der Weisheit im 9. Al-Khwarizmis vielleicht wichtigster Beitrag zur Mathematik war sein entschiedenes Eintreten für das hinduistische Zahlensystem (1 – 9 und 0), das er als leistungsfähig und effizient genug erkannte, um die islamische (und später auch die westliche) Mathematik zu revolutionieren, und das bald von der gesamten islamischen Welt und später auch von Europa übernommen wurde.
Al-Khwarizmi leistete einen weiteren wichtigen Beitrag zur Algebra. Er führte die grundlegenden algebraischen Methoden der „Reduktion“ und des „Ausgleichs“ ein und lieferte eine ausführliche Darstellung der Lösung von Polynomgleichungen bis zum zweiten Grad. Auf diese Weise trug er dazu bei, die mächtige abstrakte mathematische Sprache zu schaffen, die noch heute in der ganzen Welt verwendet wird, und ermöglichte eine viel allgemeinere Art der Analyse von Problemen als nur die spezifischen Probleme, die zuvor von den Indern und Chinesen betrachtet wurden.
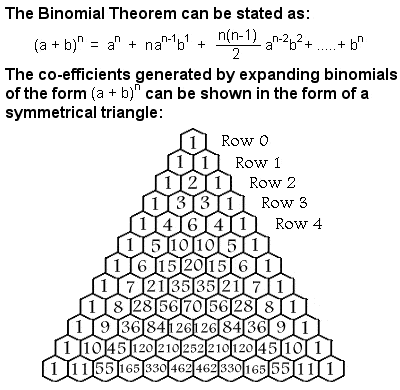
Binomischer Satz
Der persische Mathematiker Muhammad Al-Karaji aus dem 10. Jahrhundert arbeitete daran, die Algebra noch weiter zu erweitern, indem er sie von ihrem geometrischen Erbe befreite, und führte die Theorie der algebraischen Kalkulation ein. Al-Karaji war der erste, der die Methode des Beweises durch mathematische Induktion verwendete, um seine Ergebnisse zu beweisen, indem er nachwies, dass die erste Aussage in einer unendlichen Folge von Aussagen wahr ist, und dann bewies, dass, wenn eine beliebige Aussage in der Folge wahr ist, auch die nächste wahr ist.
Binomischer Satz
Unter anderem verwendete Al-Karaji die mathematische Induktion, um den binomischen Satz zu beweisen. Ein Binom ist ein einfacher algebraischer Ausdruck mit nur zwei Termen, die nur durch Addition, Subtraktion, Multiplikation und positive ganzzahlige Exponenten bearbeitet werden, wie z. B. (x + y)2. Die Koeffizienten, die bei der Erweiterung eines Binoms benötigt werden, bilden ein symmetrisches Dreieck, das gewöhnlich als Pascalsches Dreieck bezeichnet wird, nach dem französischen Mathematiker Blaise Pascal aus dem 17. Jahrhundert, obwohl viele andere Mathematiker es Jahrhunderte vor ihm in Indien, Persien, China und Italien studiert hatten, darunter auch Al-Karaji.
Einige hundert Jahre nach Al-Karaji verallgemeinerte Omar Khayyam (vielleicht besser bekannt als Dichter und Verfasser der „Rubaiyat“, aber auch ein bedeutender Mathematiker und Astronom) im frühen 12. Jahrhundert die indischen Methoden zur Gewinnung von Quadrat- und Kubikwurzeln auf vierte, fünfte und höhere Wurzeln. Er führte eine systematische Analyse der kubischen Probleme durch und stellte fest, dass es tatsächlich mehrere verschiedene Arten von kubischen Gleichungen gab. Obwohl es ihm tatsächlich gelang, kubische Gleichungen zu lösen, und obwohl ihm in der Regel die Grundlagen der algebraischen Geometrie zugeschrieben werden, wurde er durch seine Unfähigkeit, die Algebra von der Geometrie zu trennen, von weiteren Fortschritten abgehalten, und eine rein algebraische Methode für die Lösung kubischer Gleichungen musste weitere 500 Jahre und die italienischen Mathematiker del Ferro und Tartaglia abwarten.
Sphärische Trigonometrie
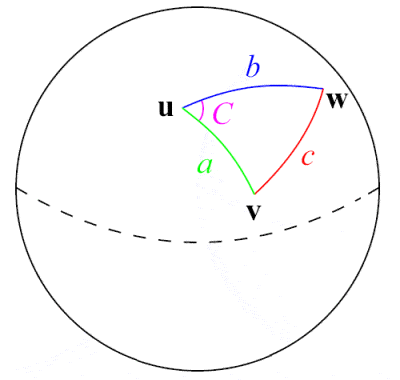
Al-Tusi war ein Pionier auf dem Gebiet der sphärischen Trigonometrie
Der persische Astronom, Wissenschaftler und Mathematiker Nasir Al-Din Al-Tusi aus dem 13. Jahrhundert war vielleicht der erste, der die Trigonometrie als eigene mathematische Disziplin behandelte, die sich von der Astronomie unterschied. Aufbauend auf früheren Arbeiten griechischer Mathematiker wie Menelaos von Alexandria und indischen Arbeiten über die Sinusfunktion gab er die erste umfassende Darstellung der sphärischen Trigonometrie, einschließlich einer Auflistung der sechs verschiedenen Fälle eines rechtwinkligen Dreiecks in der sphärischen Trigonometrie. Einer seiner wichtigsten mathematischen Beiträge war die Formulierung des berühmten Sinusgesetzes für ebene Dreiecke, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), obwohl das Sinusgesetz für sphärische Dreiecke bereits von den Persern Abul Wafa Buzjani und Abu Nasr Mansur im 10.
Weitere erwähnenswerte mittelalterliche muslimische Mathematiker sind:
- der Araber Thabit ibn Qurra aus dem 9. Jahrhundert, der eine allgemeine Formel entwickelte, mit der sich gütige Zahlen ableiten ließen, die viel später sowohl von Fermat als auch von Descartes wiederentdeckt wurden (gütige Zahlen sind Zahlenpaare, bei denen die Summe der Teiler der einen Zahl gleich der anderen Zahl ist, z. B.z. B. die richtigen Teiler von 220 sind 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 und 110, deren Summe 284 ist; und die richtigen Teiler von 284 sind 1, 2, 4, 71 und 142, deren Summe 220 ist);
- der arabische Mathematiker Abul Hasan al-Uqlidisi aus dem 10. Jahrhundert, der den frühesten erhaltenen Text schrieb, der die Verwendung von arabischen Ziffern und insbesondere die Verwendung von Dezimalzahlen anstelle von Brüchen zeigt (z. B. 7.g. 7.375 insead of 73⁄8);
- der arabische Geometer Ibrahim ibn Sinan aus dem 10. Jahrhundert, der Archimedes‘ Untersuchungen über Flächen und Volumen sowie über die Tangenten eines Kreises fortsetzte;
- der Perser Ibn al-Haytham (auch bekannt als Alhazen) aus dem 11. Jahrhundert, der neben seinen bahnbrechenden Arbeiten über Optik und Physik die Anfänge der Verbindung zwischen Algebra und Geometrie herstellte und das so genannte „Alhazen-Problem“ entwickelte (er war der erste Mathematiker, der die Formel für die Summe der vierten Potenzen ableitete und dabei eine leicht verallgemeinerbare Methode verwendete); und
- der Perser Kamal al-Din al-Farisi aus dem 13. Jahrhundert, der die Theorie der Kegelschnitte anwandte, um optische Probleme zu lösen, und der auch Arbeiten zur Zahlentheorie, wie etwa zu den gütigen Zahlen, zur Faktorisierung und zu kombinatorischen Methoden, durchführte;
- der Marokkaner Ibn al-Banna al-Marrakushi aus dem 13. Jahrhundert, zu dessen Werken Themen wie die Berechnung von Quadratwurzeln und die Theorie der fortgesetzten Brüche gehörten, sowie die Entdeckung des ersten neuen Paares gütiger Zahlen seit der Antike (17.296 und 18.416, die später von Fermat wiederentdeckt wurden) und die erste Verwendung der algebraischen Notation seit Brahmagupta.
Mit dem erstickenden Einfluss des türkischen Osmanischen Reiches ab dem 14. oder 15. Jahrhundert stagnierte die islamische Mathematik, und die weitere Entwicklung verlagerte sich nach Europa.
| << Zurück zu Madhava | Weiter zu Al-Khwarizmi >> |