Es gibt Stammbäume und Populationen, bei denen das Prinzip der panmiktischen Paarung im Wesentlichen durchbrochen ist. In der Regel handelt es sich um geographisch oder sozial relativ isolierte kleine Gemeinschaften. In diesen Gemeinschaften kann die Inzucht, d.h. die blutsverwandte Verpaarung verschiedener Ordnungen (Eltern – Kinder, Geschwister, Cousins und Cousinen, Onkel – Nichte usw.), weit verbreitet sein.
Das Problem des Einflusses der Inzucht auf die Population ist ein wichtiges Problem der Genetik 1. Jetzt hat dieses Problem noch nicht die endgültige Lösung erhalten.
In den meisten Fällen wird die Inzucht in einem Stammbaum über drei Generationen berücksichtigt. Es sind die am weitesten entfernten Verwandten, die berücksichtigt werden, bei blutsverwandten Verpaarungen sind es Cousins und Cousinen zweiten Grades.
Die Inzucht wird mit Hilfe des Inzuchtfaktors berücksichtigt.
Der Inzuchtfaktor ist die Wahrscheinlichkeit, dass zwei Allele von der Herkunft her identisch sind.
Betrachten wir die von Wright 1, 2 angebotene Methode zur Berechnung des Inzuchtfaktors in einem Stammbaum.
Für die Ermittlung des Inzuchtfaktors ist es notwendig:
Für die heiratenden Nachkommen alle Wege im Stammbaum zu finden, die durch den gemeinsamen Vorfahren diese Nachkommen verbinden.
Die Anzahl der Schritte (Generationenwechsel) auf jedem Weg zu zählen.
Dann ist der Inzuchtfaktor gleich:
 ……(1)
……(1)
wobei r die Anzahl der Wege, m1, m2, …. mi- Anzahl der Schritte auf jedem Weg.
Wir werden noch einmal feststellen, dass die Anzahl der Summanden in der Summe (1) gleich der Anzahl der Wege ist, die durch die gemeinsamen Vorfahren die Heirat verbinden.
Betrachten wir konkrete Fälle von Stammbäumen, Abbildung 1. In dieser Abbildung bedeutet das Quadrat ein männliches Individuum, der Kreis – ein weibliches Individuum. Die gestrichelten Linien und die identischen Ziffern bezeichnen die möglichen Wege im Stammbaum, die durch den gemeinsamen Vorfahren (den Mann oder die Frau) die Nachkommenschaft der Blutsverwandtschaft verbinden. Auf einigen Seiten der Wege, Bild 1с, gibt es zwei Ziffern 1 und 2. Sie gibt an, dass solche Seiten die gemeinsamen für die verschiedenen Wege sind.
Die Ehe Vater – Tochter ist Inzest, Abbildung 1а. Der Nachkomme (Frau) ist mit dem Vorfahren (Mann) dort 1 Weg mit einem Schritt verbunden, d.h. m = 1. Es gibt also einen Inzuchtfaktor.
Ft = 1/2.2-1 = 1/4
Es gibt eine Ehe Bruder – Schwester (Geschwister), Abbildung 1b. Ziffern geben die Anzahl der Wege an. Die Anzahl der identischen Ziffern auf dem Weg vom Mann zur Frau ist gleich der Anzahl der Schritte.
Lassen Sie jeden Nachkommen, der geheiratet hat, mit dem Partner zwei Wege mit zwei Schritten auf jedem Weg verbinden, d.h. m = 2. Daher gibt es einen Inzuchtfaktor.
Ft = 1/2.(2-2 + 2-2) = 1/4
Die Ehe zwischen Cousins ist auf Abbildung 1с dargestellt.
Abbildung 1. Einige Arten der Inzucht in einem Stammbaum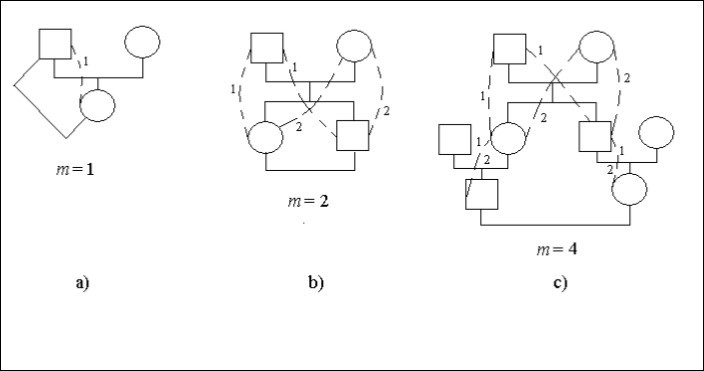
Jeder Nachkomme, der geheiratet hat, verbindet sich mit seinem Partner auf 2 Wegen mit jeweils 4 Schritten, d.h. m = 4. Folglich gibt es einen Inzuchtfaktor.
Ft = 1/2.(2-4 + 2-4) = 1/16
Die Formel (1) ist aus der folgenden Logik leicht zu verstehen.
Natürlich sind 1/2 Gene des Kindes mit jedem Elternteil gemeinsam, 1/4 – mit dem Großvater und der Großmutter, 1/8 – mit dem Urgroßvater und der Urgroßmutter, usw. Wenn von der Frau zu irgendeinem Vorfahren der Weg mit η Schritten führt, ist der Anteil der gemeinsamen Gene mit diesem Vorfahren gleich 2-η. Wenn der Weg vom Mann zu einem beliebigen Vorfahren mit μ-Schritten führt, ist der Anteil der gemeinsamen Gene gleich 2-μ. Bei der Heirat des Mannes und der Frau mit dem gemeinsamen Vorfahren wird der Anteil der gemeinsamen Gene mit diesem Vorfahren 2-η sein. 2-μ = 2-m, wobei m = η + μ die Gesamtzahl der Schritte durch den gemeinsamen Vorfahren von der Frau bis zur Heirat des Mannes ist. Die Größe 1/2 2-m gibt die Wahrscheinlichkeit an, dass das bei der Frau zufällig ausgewählte Gen vom Ursprung her mit dem beim Mann zufällig ausgewählten Gen identisch ist. Die gleiche Größe gibt den Beitrag zum Inzuchtfaktor Ft in einer Richtung durch den gemeinsamen Vorfahren von der Frau bis zur Heirat des Mannes an.
Wenn zum Beispiel der gemeinsame Vorfahre η = μ = 5 Generationen von der Heirat entfernt ist, ist die Wahrscheinlichkeit, dass sie das gemeinsame Gen haben, gleich. 1/2 2-(5+5) = 1/2048 Diese Größe kann bei der Analyse der Paarung vernachlässigt werden. (Tabelle 1)
Tabelle 1.Inzuchtfaktoren für einige blutsverwandte Ehen sind zusätzlich dargestellt.
| Die Art der blutsverwandten Ehe | Inzuchtfaktor Ft |
| Cousins und Cousinen zweiten Grades | 1/32 |
| Cousin Onkel – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: Der Ursprung identischer Allele in homologen Autosomen ist nicht-konsanguinisch (die Wahrscheinlichkeit dieser Hypothese ist P(H1) = 1- Ft )auch entsteht homozygoteаа (die bedingte Wahrscheinlichkeit dieses Ereignisses ist P(aa/H1) = q2) oder der Ursprung identischer Allele ist konsanguinisch (die Wahrscheinlichkeit dieser Hypothese ist P(H2) = Ft ) und es entsteht homozygoteаа (die bedingte Wahrscheinlichkeit dieses Ereignisses ist P(aa/H2) = q). Die Wahrscheinlichkeit q des Auftretens des Homozygoten aa im letzteren Fall wird dadurch bestimmt, dass, wenn sich das Allel a in einem Autosom befindet, bei blutsverwandtem Ursprung des Homozygoten dasselbe Allel notwendigerweise im homologen Autosom sein sollte.
Die Gesamtwahrscheinlichkeit des rezessiven homozygoten Auftretens ist also gleich:
 ……….(3)
……….(3)
Dabei gilt p = 1 – q für die Häufigkeit des dominanten Allels a.
Gleichermaßen ergibt sich die Gesamtwahrscheinlichkeit des Auftretens des dominanten Homozygoten AA bei zufälliger Verpaarung:
 ……….. (4)
……….. (4)
Nach (3) und (4) steigt also die Gesamthäufigkeit der Homozygoten (dominant und rezessiv) im Inzuchtstammbaum auf 2Ftpq. Die Häufigkeit der Heterozygoten nimmt also bei gleicher Größe ab und wird gleich 2pq – 2pqFt = 2pq(1-Ft), da die Summe aller Zygotenhäufigkeiten gleich 1 ist.
In Anbetracht des Inzuchtfaktors sowie (3) und (4) muss das Hardy-Weinberg-Gesetz in der folgenden Generation des Inzuchtstammbaums für ein autosomales Genom die Verteilungen der Zygotengenotypen als 4 notiert werden:
 …………(5)
…………(5)
Wobei pn die Häufigkeit der dominanten Allele A in Generation n ist, qn – die Häufigkeit der rezessiven Allele a, also pn + qn = 1.
Das Verhältnis (5) bezieht sich auch auf das Wright’sche Verhältnis 5. Das Wright’sche Verhältnis zeigt, dass in einem Inzuchtstammbaum nach der blutsverwandten Verpaarung von Individuen folgende Effekte zu beobachten sind: es gibt eine Zunahme des autosomalen Homozygotenanteils in einem Stammbaum auf Ft pnqnund eine Abnahme des autosomalen Heterozygotenanteils in (1-F1) im Vergleich zu einer panmiktischen Population.
Aber schon durch eine Generation wird das Hardy-Weinberg-Gleichgewicht wiederhergestellt, das die geringe Bedeutung der getrennten blutsverwandten Verpaarung für einen Stammbaum angibt:
 ………(6)
………(6)
Natürlich wird für eine Population als Ganzes der getrennte Akt der blutsverwandten Verpaarung noch geringere Bedeutung haben als für einen Stammbaum.
Der gleiche Effekt wird bei der Variation der Häufigkeit der Zygotengenotypen und bei geschlechtsgebundenen Genen beobachtet.
Die Verteilung der an das Х-Chromosom gebundenen Genotypen in einem panmiktischen Stammbaum wird durch das Hardy-Weinberg-Gesetz als 1 beschrieben:
 ………..(7)
………..(7)
Die Häufigkeit eines dominanten Allels A bezeichnen wir bei den Männern pm und bei den Frauen pf. Für rezessive Allelea sind es entsprechend qm und qf.
Bei der Paarung ergibt sich bei den Frauen ein Verhältnis der Genotypen entsprechend dem Produkt (pf + qf) (pm +qm).
Bestimmen wir die Gesamtwahrscheinlichkeit des Auftretens der rezessiven Homozygote aa bei zufälliger Paarung für die mit demХ-Chromosom verbundenen Gene der Tochter nach der Formel (2). Die Logik der Ereignisse ist ähnlich wie bei den Autosomen, mit der Ausnahme, dass die bedingte Wahrscheinlichkeit des Auftretens des Genotypsаа der nicht-konsanguinen Allele gemäß (7) gleich P(aa/H1) = qmnqfn ist. Für die konsanguinen Allele ist die bedingte Wahrscheinlichkeit des Auftretens des Genotypsаа gleich P(aa/H2) = qf(n+1). Bei den Töchtern, d.h. in der Generation n+1, wird die Wahrscheinlichkeit des Auftretens des Homozygoten aa dadurch bestimmt, dass, wenn das Allel a in einem Х-Chromosom vorhanden ist, bei der blutsverwandten Herkunft des Homozygoten dasselbe Allel notwendigerweise im homologen Х-Chromosom vorhanden sein muss.
Die Gesamtwahrscheinlichkeit des Auftretens des rezessiven Homozygoten ist also gleich:
 ……(8)
……(8)
wobei pmn die Häufigkeit des dominanten Allels a in der Generation n bei Männern und pfn – bei Frauen ist. Für die rezessiven Allele a entsprechend qmn und qfn . Dabei wird qmn =1 – qmn und pfn = 1 – qfn verwendet.
Auch das Finden der Gesamtwahrscheinlichkeit des dominanten homozygoten Auftretens mit Hilfe:
 ,
,
 ……….(9)
……….(9)
und einem Heterozygoten P(Aa) = 1- P(aa) – P(AA) finden wir die Verteilung der Genotypen in den Х-Chromosomen des Inzuchtstammbaums bei der Paarung:
 ……..(10)
……..(10)
Gleichzeitig wird gezeigt, dass die Inzuchtadditionen in den dominanten und rezessiven Homozygotenhäufigkeiten in den geschlechtsgebundenen Chromosomen identisch sind wie bei den Autosomen.
Eine andere Art, das Verhältnis (10) zu finden, besteht im Folgenden.
Bestimmen wir zunächst die Gesamtwahrscheinlichkeit des Auftretens einer Heterozygote Aa, d.h. P(Aa) bei der Gelegenheit der zufälligen blutsverwandten Verpaarung. Diese Wahrscheinlichkeit ergibt sich aus der folgenden Logik der Paarung: Wenn der Ursprung der Allele nicht konsanguinisch ist (die Wahrscheinlichkeit dieser Hypothese ist P(H1) = 1 – Ft ) entsteht auch das Heterozygote Aа (die bedingte Wahrscheinlichkeit dieses Ereignisses ist P(Aa/H1) = pmnqfn + pfnqmn, siehe Formel (7)) oder der Ursprung der Allele ist blutsverwandt (die Wahrscheinlichkeit dieser Hypothese ist P(H2) = Ft) und es entsteht die Heterozygote Aа (die bedingte Wahrscheinlichkeit dieses Ereignisses ist gleich Null P(Aa/H2) = 0 ). Die letzte Aussage ist dadurch definiert, dass bei blutsverwandter Abstammung ähnliche Allele in homologen Х-Chromosomen nicht die HeterozygoteАа entstehen können, die aus verschiedenen Allelen besteht.
Daher finden wir mit der Formel der Gesamtwahrscheinlichkeit die Gesamtwahrscheinlichkeit des Auftretens der Heterozygote Aa:
 …….(11)
…….(11)
Die Verringerung der Häufigkeit der Heterozygoten Aa erfolgt, wie bereits bewiesen wurde, durch die identische Zunahme der Häufigkeit der dominanten AA- und rezessiven aa-Homozygoten. Zum Beispiel ist die Zunahme der rezessiven aa-Homozygotenfrequenz gleich:
 ……..(12)
……..(12)
wobei die Reduktion der Heterozygoten Aa-Häufigkeit relativ zum panmiktischen Stammbaum gemäß (7) und (11) gleich ist. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) Unter Verwendung von (11) und (12) zur Aktualisierung von (7) für Fälle von Inzucht finden wir die Verteilung der Genotypen (10) in Х-Chromosomen im Inzuchtstammbaum der Töchter.
In der folgenden Generation ist die Häufigkeit der rezessiven Allele a bei den Frauen gleich:
 ……..(13)
……..(13)
Das entspricht vollständig der gleichen Häufigkeit bei Abwesenheit von Inzucht, d.h. es gibt eine Wiederherstellung des Hardy-Weinberg-Gleichgewichts oder eine genauere Annäherung an das Gleichgewicht.
Die Verhältnisse (7) und (13) zeigen insgesamt, dass sich die Allelhäufigkeiten in einem Stammbaum bei Inzucht nicht verändern. Es findet lediglich eine Allelumverteilung statt. Ein Teil der Allele verlässt die Heterozygoten und geht auf die Homozygoten über.