Verwendung von Instrumentalvariablen zum Nachweis der Kausalität

Vorteile der Verwendung von Instrumentalvariablen zum Nachweis der Kausalität

Betrachten wir als Beispiel das Problem der Schätzung der Auswirkung von Bildung auf das Einkommen. Die einfachste Schätzmethode, die gewöhnliche kleinste Quadrate (OLS), führt zu Schätzungen, die darauf hinweisen, dass ein zusätzliches Jahr Bildung mit einem um 6-10 % höheren Verdienst verbunden ist. Die positive Beziehung kann jedoch auch auf die Selbstselektion in die Ausbildung zurückzuführen sein, d. h. Personen, die am meisten von einer höheren Ausbildung profitieren, bleiben mit größerer Wahrscheinlichkeit in der Ausbildung. Dies ist beispielsweise der Fall, wenn Schülern mit höheren Fähigkeiten das Lernen leichter fällt und sie wahrscheinlich ohnehin höhere Löhne erhalten würden. Somit würde die beobachtete positive Korrelation zwischen Bildungsjahren und Löhnen teilweise die Prämie für Fähigkeiten widerspiegeln und könnte nicht, wie beabsichtigt, als Ertrag eines zusätzlichen Bildungsjahres interpretiert werden. OLS-Schätzungen wären daher nicht aussagekräftig in Bezug auf die Auswirkungen einer Politik, die auf eine Erhöhung der Ausbildungsjahre abzielt. Dieses Problem wird als „omitted variable bias“ bezeichnet. Es tritt auf, wenn eine Variable (z. B. die Fähigkeit), die vom Forscher nicht beobachtet wird, sowohl mit der Behandlung (mehr Bildung) als auch mit dem Ergebnis (Einkommen) korreliert. Die Richtung (Über- oder Unterschätzung) und das Ausmaß der Verzerrung in OLS-Schätzungen ist eine Funktion des Vorzeichens und der Stärke der Korrelationen.

In diesem Beispiel ist ein randomisierter Kontrollversuch (RCT), bei dem die Bildung nach dem Zufallsprinzip auf die einzelnen Personen aufgeteilt und die Unterschiede in den Löhnen über die gesamte Lebenszeit beobachtet würden, aus ethischen Gründen einfach nicht durchführbar. Einige natürliche oder quasi-natürliche Experimente kommen jedoch einer Veränderung der Bildungsentscheidungen für bestimmte Personengruppen sehr nahe und können daher als Instrumente verwendet werden. Ein solches natürliches Experiment ist die Änderung des gesetzlichen Mindestalters, in dem Schüler die Schule verlassen dürfen (Schulabschlussalter). Diese Art von Veränderung betrifft alle Schüler, unabhängig von ihren Fähigkeiten. Sie wirkt daher wie ein externer Schock, der vom einzelnen Schüler nicht beeinflusst werden kann.

Zahlreiche Länder haben Gesetze, die das Alter festlegen, in dem Schüler das Bildungssystem verlassen können. Nehmen wir zum Beispiel an, dass ein Kind die Schule am letzten Tag des Schuljahres verlassen kann, wenn es Ende August 14 Jahre alt ist. Nehmen wir nun an, dass die Rechtsvorschriften dahingehend geändert werden, dass die Kinder Ende August 15 Jahre alt sein müssen, um die Schule verlassen zu können. Kinder, die die Schule mit 14 Jahren verlassen wollten, werden daran gehindert und müssen ein weiteres Jahr zur Schule gehen. Unter der (starken) Annahme, dass die Kinder unter den beiden Gesetzgebungen ähnlich sind und ähnlichen Arbeitsmarktbedingungen ausgesetzt sind, führt die Gesetzesänderung zu einem quasi-natürlichen Experiment: Unabhängig von ihren Fähigkeiten werden einige Personen von der Änderung des Schulabgangsalters betroffen sein und ein zusätzliches Jahr in der Schule bleiben müssen, während Schüler mit ähnlichen Präferenzen aus der vorherigen Kohorte dies nicht tun. Wenn die Forscher wüssten, wer die Schule mit 14 Jahren verlassen wollte, könnten sie die Ergebnisse von Personen, die die Schule mit 14 Jahren verlassen haben, mit den Ergebnissen von Personen vergleichen, die gezwungen waren, bis 15 zu bleiben. Dieser einfache Unterschied wäre dann der kausale Effekt des Verbleibs in der Schule zwischen 14 und 15 Jahren. Leider erlauben es uns die Beobachtungsdaten nicht, die Personen zu identifizieren, deren Bildungsentscheidungen durch die Reform beeinflusst wurden; daher sind Personen, die die Schule mit 15 Jahren verlassen wollten, nach der neuen Gesetzgebung nicht von denjenigen zu unterscheiden, die die Schule mit 14 Jahren verlassen wollten, aber noch ein Jahr länger bleiben mussten. Was die Reform jedoch bewirkt, ist eine Änderung der Wahrscheinlichkeit, in der Schule zu bleiben, und kann daher als Instrument verwendet werden, da sie die Wahrscheinlichkeit einer Behandlung (ein weiteres Schuljahr) beeinflusst, ohne das interessierende Ergebnis (z. B. den Verdienst) zu beeinflussen.

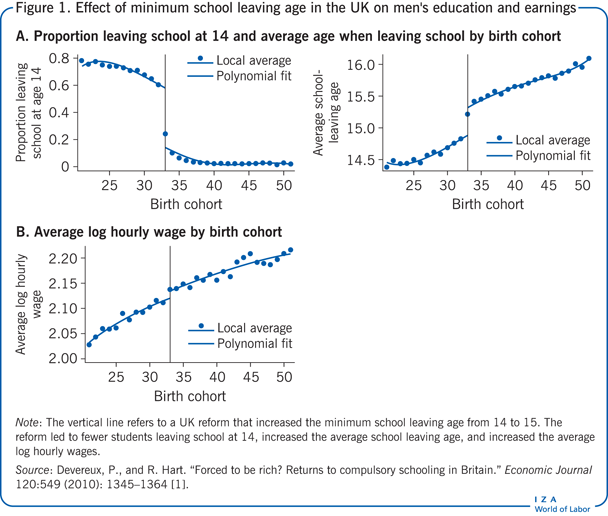
Im Jahr 1947 wurde durch eine Gesetzesänderung im Vereinigten Königreich das Mindestalter für den Schulabschluss von 14 auf 15 Jahre angehoben, was Kinder betraf, die 1933 und später geboren wurden. Diese Gesetzesänderung bietet die Möglichkeit, die Auswirkungen der (zusätzlichen) Schulbildung auf den Verdienst zu untersuchen. Abbildung 1, Feld A zeigt, dass sich die Reform sowohl auf den Anteil der Kinder auswirkte, die die Schule zum frühestmöglichen Zeitpunkt verließen (linkes Diagramm), als auch auf den Gesamtumfang der abgeschlossenen Schulbildung (rechtes Diagramm). Die Schätzungen zeigen, dass die Reform die durchschnittlichen Schuljahre für Männer um 0,397 Jahre erhöht hat. Diese Schätzung des Effekts der Reform (die IV) auf die Behandlung (Bildung) wird als „Regression der ersten Stufe“ bezeichnet. Wenn die Bildung einen kausalen Effekt auf den Verdienst hat, sollten wir feststellen, dass der durchschnittliche Verdienst der von der Reform betroffenen Personen ebenfalls höher ist. Dies ist in der Tat der Fall, wie aus Feld B von Abbildung 1 hervorgeht, in dem der durchschnittliche logarithmierte Verdienst von Männern dargestellt ist. Diese Reihe zeigt einen klaren Bruch im Jahr 1933, dessen Ausmaß bedeutet, dass die von der Reform betroffenen Personen im Durchschnitt 1,2 % mehr verdienen. Diese zweite Schätzung der Auswirkungen der Reform (die IV) auf das Ergebnis (Verdienst) wird als „Schätzung in reduzierter Form“ bezeichnet. Eine einfache IV-Strategie, in diesem Fall unter Verwendung eines binären Instruments, das nur zwei Werte annimmt (1, wenn es von der Reform betroffen ist, und 0, wenn es nicht von der Reform betroffen ist), ist das Verhältnis der Schätzung der reduzierten Form zur Schätzung der ersten Stufe. (Dieses Verhältnis wird auch als Wald-Schätzung bezeichnet.) In diesem Fall wäre der kausale Effekt von zusätzlicher Bildung auf den Verdienst 0,012/0,397 = 0,030 und damit etwa 3%.

Die Intuition dieses Ansatzes besteht darin, dass der Effekt eines zusätzlichen Bildungsjahres auf den Verdienst im Grunde genommen der Effekt der Reform (die IV) auf den Verdienst (das Ergebnis) ist – der in der reduzierten Form gegeben ist – hochskaliert mit dem Effekt, den die Reform auf die Bildungsjahre hat (die Behandlung) – worum es bei der Schätzung der ersten Stufe geht. Wenn das Instrument „relevant“ ist, d. h. einen Effekt auf die Bildung (die Behandlung) hat, und wenn das Instrument die Löhne „ausschließlich“ durch seinen Effekt auf die Bildung beeinflusst, dann können die IV-Schätzungen als kausaler Effekt der Behandlung auf das Ergebnis interpretiert werden. Diese beiden Bedingungen werden als „Instrumentenrelevanz“ und „Ausschlussbeschränkung“ bezeichnet.

Zusammenfassend lässt sich sagen, dass eine einfache Schätzung wie OLS aufgrund der Selbstselektion in die Behandlung verzerrt ist, wenn eine unbeobachtete Variable wie die Fähigkeit sowohl mit der Behandlung als auch mit dem Ergebnis korreliert. Ähnlich verhält es sich, wenn die Behandlungsvariable mit Fehlern gemessen wird und die OLS-Schätzung gegen Null verzerrt ist. Eine kausale Schätzung der Auswirkungen einer Behandlung auf ein Ergebnis kann jedoch ermittelt werden, wenn ein glaubwürdiges Instrument gefunden werden kann. Ein glaubwürdiges Instrument muss zwei Bedingungen erfüllen:

• Relevanz: Das Instrument muss die Wahrscheinlichkeit der Behandlung beeinflussen. In einer Regression der Behandlung auf das Instrument, auch bekannt als Gleichung der ersten Stufe, muss der Koeffizient auf die IV hinreichend stark sein.

• Ausschlussrestriktion: Das Instrument beeinflusst das Ergebnis ausschließlich über seinen Effekt auf die Behandlung.

Wenn eine solche IV gefunden werden kann (d.h..

Wenn eine solche IV gefunden werden kann (d.h. sowohl die Relevanz- als auch die Ausschlussrestriktion sind erfüllt), dann kann eine IV-Strategie implementiert werden, um einen kausalen Effekt der Behandlung auf das Ergebnis zu ermitteln.

Im vorherigen Beispiel wurde die Wald-Schätzung vorgestellt, d.h. das Verhältnis der Schätzungen aus zwei Regressionen: die Schätzung in reduzierter Form, die aus einer Regression des Ergebnisses auf das Instrument stammt, und die Schätzung der ersten Stufe, die aus einer Regression der Behandlung auf das Instrument stammt. Dies kann leicht berechnet werden, wenn das Instrument nur zwei Werte annimmt. Im allgemeineren Fall wird eine so genannte „zweistufige Kleinstquadrate“-Schätzung (2SLS) berechnet, wobei die Vorhersagen der Behandlung aus der Gleichung der ersten Stufe in einer Regression des Ergebnisses auf die Behandlung verwendet werden und nicht der wahre Wert der Behandlung. Somit wird nur die aus dem Instrument stammende Variation der Behandlung zur Erklärung der Varianz des Ergebnisses verwendet. Auf diese Weise wird die Verzerrung durch Selbstselektion beseitigt. Im Falle eines binären (zweiwertigen) Instruments sind die Wald- und 2SLS-Schätzungen identisch (siehe z. B. …). Die Schwierigkeit liegt jedoch nicht in der Durchführung einer solchen 2SLS-Schätzung – alle Statistikpakete können IV-Schätzungen berechnen – sondern in (a) der Suche nach einem gültigen Instrument und (b) der Interpretation der Ergebnisse. Die Diskussion wird sich nun auf diese beiden Punkte konzentrieren.