Contents
- A Brief History of Perceptrons
- Multilayer Perceptrons
- Just Show Me the Code
- FootNotes
- Further Reading
A Brief History of Perceptrons
The perceptron, that neural network whose name evokes how the future looked from the perspective of the 1950s, is a simple algorithm intended to perform binary classification; i.e. it predicts whether input belongs to a certain category of interest or not: fraud or not_fraudcat or not_cat.
Le perceptron occupe une place particulière dans l’histoire des réseaux neuronaux et de l’intelligence artificielle, car le battage initial autour de ses performances a conduit à une réfutation par Minsky et Papert, et à une réaction plus large qui a jeté un froid sur la recherche sur les réseaux neuronaux pendant des décennies, un hiver des réseaux neuronaux qui n’a totalement dégelé qu’avec les recherches de Geoff Hinton dans les années 2000, dont les résultats ont depuis balayé la communauté de l’apprentissage automatique.
Frank Rosenblatt, parrain du perceptron, l’a popularisé comme un dispositif plutôt qu’un algorithme. Le perceptron est d’abord entré dans le monde sous forme de matériel.1 Rosenblatt, un psychologue qui a étudié puis enseigné à l’Université Cornell, a reçu un financement de l’Office of Naval Research des États-Unis pour construire une machine capable d’apprendre. Sa machine, le perceptron Mark I, ressemblait à ceci.

Un perceptron est un classificateur linéaire, c’est-à-dire un algorithme qui classe les entrées en séparant deux catégories par une ligne droite. L’entrée est généralement un vecteur de caractéristiques x multiplié par des poids w et ajouté à un biais by = w * x + b.
Un perceptron produit une sortie unique basée sur plusieurs entrées à valeur réelle en formant une combinaison linéaire à l’aide de ses poids d’entrée (et en faisant parfois passer la sortie par une fonction d’activation non linéaire). Voici comment vous pouvez écrire cela en mathématiques :
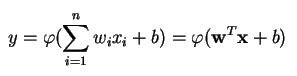
où w désigne le vecteur des poids, x est le vecteur des entrées, b est le biais et phi est la fonction d’activation non linéaire.
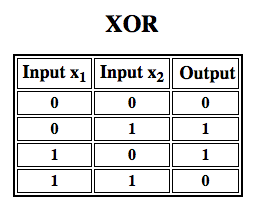
Rosenblatt a construit un perceptron à une seule couche. C’est-à-dire que son matériel-algorithme ne comprenait pas de couches multiples, qui permettent aux réseaux neuronaux de modéliser une hiérarchie de caractéristiques. Il s’agissait donc d’un réseau neuronal peu profond, ce qui empêchait son perceptron d’effectuer une classification non linéaire, comme la fonction XOR (un opérateur XOR se déclenche lorsque l’entrée présente soit un trait, soit un autre, mais pas les deux ; il signifie » OU exclusif « ), comme l’ont montré Minsky et Papert dans leur livre.
Appliquer l’apprentissage par renforcement aux simulations »
Perceptrons multicouches (MLP)
Des travaux ultérieurs sur les perceptrons multicouches ont montré qu’ils étaient capables d’approximer un opérateur XOR ainsi que de nombreuses autres fonctions non linéaires.
De même que Rosenblatt a basé le perceptron sur un neurone McCulloch-Pitts, conçu en 1943, de même, les perceptrons eux-mêmes sont des blocs de construction qui ne s’avèrent utiles que dans des fonctions aussi grandes que les perceptrons multicouches2.)
Le perceptron multicouche est le bonjour du monde de l’apprentissage profond : un bon point de départ lorsque vous vous initiez à l’apprentissage profond.
Un perceptron multicouche (MLP) est un réseau neuronal artificiel profond. Il est composé de plus d’un perceptron. Ils sont composés d’une couche d’entrée pour recevoir le signal, une couche de sortie qui prend une décision ou une prédiction sur l’entrée, et entre ces deux, un nombre arbitraire de couches cachées qui sont le véritable moteur de calcul du MLP. Les MLP à une couche cachée sont capables d’approximer n’importe quelle fonction continue.
Les perceptrons multicouches sont souvent appliqués à des problèmes d’apprentissage supervisé3 : ils s’entraînent sur un ensemble de paires d’entrées-sorties et apprennent à modéliser la corrélation (ou les dépendances) entre ces entrées et ces sorties. L’apprentissage consiste à ajuster les paramètres, ou les poids et les biais, du modèle afin de minimiser l’erreur. La rétropropagation est utilisée pour effectuer ces ajustements de poids et de biais par rapport à l’erreur, et l’erreur elle-même peut être mesurée de diverses manières, notamment par l’erreur quadratique moyenne (RMSE).
Les réseaux à action directe tels que les MLP sont comme le tennis, ou le ping-pong. Ils effectuent principalement deux mouvements, un va-et-vient constant. Vous pouvez penser à ce ping-pong de suppositions et de réponses comme une sorte de science accélérée, puisque chaque supposition est un test de ce que nous pensons savoir, et chaque réponse est une rétroaction nous faisant savoir à quel point nous nous trompons.
Dans le passage en avant, le flux de signaux passe de la couche d’entrée à la couche de sortie en passant par les couches cachées, et la décision de la couche de sortie est mesurée par rapport aux étiquettes de vérité terrain.
Dans le passage en arrière, en utilisant la rétropropagation et la règle de chaîne du calcul, les dérivées partielles de la fonction d’erreur par rapport aux différents poids et biais sont rétropagées à travers le MLP. Cet acte de différenciation nous donne un gradient, ou un paysage d’erreur, le long duquel les paramètres peuvent être ajustés pour rapprocher le MLP du minimum d’erreur. Cela peut être fait avec n’importe quel algorithme d’optimisation basé sur le gradient, comme la descente de gradient stochastique. Le réseau continue à jouer cette partie de tennis jusqu’à ce que l’erreur ne puisse pas descendre plus bas. Cet état est connu sous le nom de convergence.
Notes de bas de page
1) La chose intéressante à souligner ici est que le logiciel et le matériel existent sur un organigramme : le logiciel peut être exprimé en tant que matériel et vice versa. Lorsque des puces telles que les FPGA sont programmées, ou que des ASIC sont construits pour cuire un certain algorithme dans le silicium, nous implémentons simplement le logiciel un niveau plus bas pour le faire fonctionner plus rapidement. De même, ce qui est cuit dans le silicium ou câblé avec des lumières et des potentiomètres, comme le Mark I de Rosenblatt, peut également être exprimé symboliquement dans un code. C’est pourquoi Alan Kay a déclaré : « Les personnes qui s’intéressent vraiment aux logiciels devraient fabriquer leur propre matériel ». Mais il n’y a pas de repas gratuit, c’est-à-dire que ce que vous gagnez en vitesse en intégrant des algorithmes dans du silicium, vous le perdez en flexibilité, et vice versa. Il s’agit d’un véritable problème en ce qui concerne l’apprentissage automatique, puisque les algorithmes se modifient eux-mêmes en fonction des données. Le défi consiste à trouver les parties de l’algorithme qui restent stables même si les paramètres changent ; par exemple, les opérations d’algèbre linéaire qui sont actuellement traitées le plus rapidement par les GPU.
2) Vos pensées peuvent incliner vers la prochaine étape d’algorithmes toujours plus complexes et aussi plus utiles. Nous passons d’un neurone à plusieurs, appelés couche ; nous passons d’une couche à plusieurs, appelés perceptron multicouche. Pouvons-nous passer d’un MLP à plusieurs, ou devons-nous simplement continuer à empiler les couches, comme l’a fait Microsoft avec son vainqueur d’ImageNet, ResNet, qui comptait plus de 150 couches ? Ou bien la bonne combinaison de MLP est-elle un ensemble de nombreux algorithmes votant dans une sorte de démocratie informatique sur la meilleure prédiction ? Ou bien est-ce l’intégration d’un algorithme dans un autre, comme nous le faisons avec les réseaux convolutifs à graphes ?
3) Ils sont largement utilisés chez Google, qui est probablement l’entreprise d’IA la plus sophistiquée au monde, pour un large éventail de tâches, malgré l’existence de méthodes plus complexes et à la pointe de la technologie.
Lecture complémentaire
- Le perceptron : Un modèle probabiliste de stockage et d’organisation de l’information dans le cerveau, Cornell Aeronautical Laboratory, Psychological Review, par Frank Rosenblatt, 1958 (PDF)
- Un calcul logique des idées immanentes à l’activité nerveuse, W. S. McCulloch & Walter Pitts, 1943
- Perceptrons : Une introduction à la géométrie computationnelle, par Marvin Minsky & Seymour Papert
- Multi-couches (MLP)
- Théorie hébraïque
Autres articles du wiki Pathmind
- Réseaux neuronaux profonds
- Réseaux neuronaux récurrents (RNNs) et L. L. Networks (RNNs) and LSTMs
- Word2vec and Neural Word Embeddings
- Convolutional Neural Networks (CNNs) and Image Processing
- Accuracy, Precision and Recall
- Attention Mechanisms and Transformers
- Eigenvectors, Eigenvalues, PCA, Covariance and Entropy
- Graph Analytics and Deep Learning
- Symbolic Reasoning and Machine Learning
- Markov Chain Monte Carlo, AI and Markov Blankets
- Deep Reinforcement Learning
- Generative Adversarial Networks (GANs)
- AI vs Machine Learning vs Deep Learning