Il existe des arbres généalogiques et des populations où le principe d’accouplement panmictique est essentiellement rompu. Il s’agit généralement de petites communautés relativement isolées géographiquement ou socialement. Dans ces communautés, la consanguinité c’est-à-dire l’accouplement consanguin de différents ordres (un parent – un enfant, des fratries, des cousins, un oncle – une nièce, etc.), peut être très répandue.
Le problème de l’influence de la consanguinité sur la population est le problème important de la génétique 1. Or ce problème n’a pas encore reçu la solution définitive.
Dans la plupart des cas, la consanguinité dans un arbre généalogique prend en compte sur trois générations. Ce sont les parents les plus éloignés qui sont pris en compte à l’accouplement consanguin il y a des cousins germains.
La consanguinité est prise en compte à l’aide du facteur de consanguinité.
Le facteur de consanguinité est la probabilité que deux allèles soient identiques par origine.
Envisageons la méthode de calcul du facteur de consanguinité dans un arbre généalogique proposée par Wright 1, 2.
Pour trouver le facteur de consanguinité il faut :
de trouver pour les descendants mariés toutes les voies d’un arbre généalogique qui, par l’ancêtre commun, relient ces descendants.
de compter le nombre d’étapes (alternances de générations) sur chaque voie.
Alors le facteur de consanguinité est égal:
 ……(1)
……(1)
où r il y a le nombre de voies, m1, m2, …. mi- nombre d’étapes sur chaque voie.
Une fois de plus, nous noterons que le nombre d’additions dans la somme (1) est égal au nombre de voies qui, à travers les ancêtres communs, relient les mariages.
Envisageons des cas concrets d’arbres généalogiques, la figure 1. Dans cette figure, le carré signifie un individu masculin le cercle – individu féminin. Les lignes en pointillés et les chiffres identiques spécifient les voies possibles dans un arbre généalogique qui, par l’intermédiaire de l’ancêtre commun (l’homme ou la femme) connecter des descendants consanguins mariage. Sur certains sites de chemins, Figure 1с, il y a deux chiffres 1 et 2. Il précise que ces sites sont le commun pour les différentes voies.
Le mariage un père – fille est l’inceste, Figure 1а. Le descendant (femme) est relié à l’ancêtre (homme) là 1 voie avec un pas, c’est-à-dire m = 1. Par conséquent, il y a un facteur de consanguinité.
Ft = 1/2,2-1 = 1/4
Il y a le mariage un frère – sœur (sibs), Figure 1b. Les chiffres précisent le numéro de la voie. Le nombre de chiffres identiques sur le chemin de l’homme qui se marie à la femme est égal au nombre d’étapes.
Laissons chaque descendant qui s’est marié se connecte avec son partenaire de deux manières avec deux étapes sur chaque chemin, soit m = 2. Par conséquent, il y a un facteur de consanguinité.
Ft = 1/2.(2-2 + 2-2) = 1/4
Le mariage entre cousins est représenté sur la figure 1с.
Figure 1. Quelques types de consanguinité dans un arbre généalogique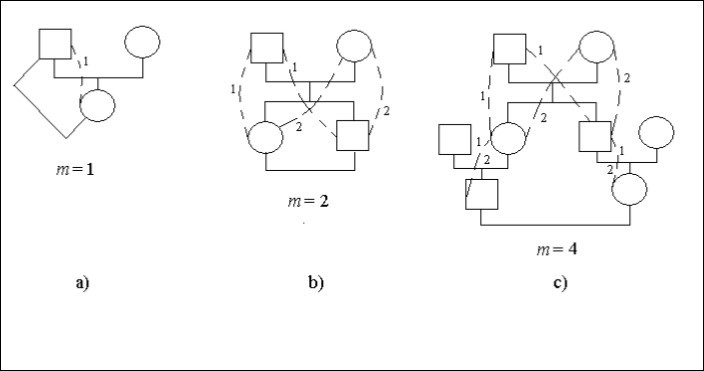
Chaque descendant qui s’est marié se connecte avec son partenaire les 2 voies avec 4 étapes sur chaque voie, soit m = 4. Par conséquent, il existe un facteur de consanguinité.
Ft = 1/2.(2-4 + 2-4) = 1/16
La formule (1) est facile à comprendre à partir de la logique suivante.
Evidemment, il y a 1/2 gènes de l’enfant est le commun avec chaque parent, 1/4 – avec le grand-père et la grand-mère, 1/8 – avec l’arrière-grand-père et l’arrière-grand-mère, etc. Si de la femme à n’importe quel ancêtre mène le chemin avec η étapes la part des gènes communs avec cet ancêtre est égale 2-η. Si de l’homme à un ancêtre quelconque, le chemin est parcouru avec μ pas, la part des gènes communs est égale à 2-μ. Lors du mariage de l’homme et de la femme avec l’ancêtre commun, la part des gènes communs avec cet ancêtre sera égale à 2-η. 2-μ = 2-m où m = η + μ il y a le nombre total d’étapes de l’ancêtre commun depuis la femme jusqu’au mariage de l’homme. La taille 1/2 2-m indique la probabilité que le gène choisi fortuitement chez la femme soit identique par origine au gène choisi fortuitement chez l’homme. La même taille donne la contribution au facteur de consanguinité Ft à sens unique par l’ancêtre commun de la femme jusqu’à l’homme se mariant.
Par exemple, si l’ancêtre commun sera éloigné du mariage sur η = μ = 5 générations la probabilité qu’ils aient le gène commun est égale. 1/2 2-(5+5) = 1/2048 Cette taille à l’analyse de l’accouplement peut être négligée. (Tableau 1)
Tableau 1.Les facteurs de consanguinité pour les quelques mariages consanguins sont indiqués en plus.
| Le type de mariage consanguin. consanguin | Facteur de consanguinité Ft |
| Cousins au second degré | 1/32 |
| Cousin oncle – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: l’origine des allèles identiques dans les autosomes homologues est non consanguine (la probabilité de cette hypothèse est P(H1) = 1- Ft )et naît également l’homozygoteаа (la probabilité conditionnelle de cet événement est P(aa/H1) = q2) ou l’origine des allèles identiques est consanguine (la probabilité de cette hypothèse est P(H2) = Ft ) et naît l’homozygoteаа (la probabilité conditionnelle de cet événement est P(aa/H2) = q). La probabilité q de l’apparition de l’homozygote aa dans ce dernier cas est déterminée par le fait que si l’allèle a est dans un autosome alors à l’origine consanguine de l’homozygote le même allèle doit nécessairement être et dans l’autosome homologue.
Donc, la probabilité totale de l’apparition de l’homozygote récessif est égale :
 ……….(3)
……….(3)
où l’on tient compte de p = 1 – q il y a la fréquence de l’allèle a dominant.
De même, on trouve la probabilité totale d’apparition de l’homozygote dominant AA lors d’un accouplement aléatoire :
 ………… (4)
………… (4)
Donc, selon (3) et (4) la fréquence totale des homozygotes (dominants et récessifs) dans l’arbre généalogique consanguin augmente sur 2Ftpq. Par conséquent, la fréquence des hétérozygotes diminue pour la même taille et pour devenir égale à 2pq – 2pqFt = 2pq(1-Ft) puisque la somme des fréquences de tous les zygotes est égale à 1.
Au vu du facteur de consanguinité et aussi de (3) et (4) la loi de Hardy – Weinberg dans la génération suivante de l’arbre généalogique consanguin pour un génome autosomique doit être écrite les distributions des génotypes des zygotes comme 4 :
 …………(5)
…………(5)
Où pn est la fréquence des allèles A dominants dans la génération n, qn – la fréquence des allèles a récessifs, donc pn + qn = 1.
Le rapport (5) se réfère aussi au rapport 5 de Wright, qui montre que dans un arbre généalogique consanguin après l’accouplement consanguin des individus sont observés les effets suivants : il y a augmentation de la fraction d’homozygotes autosomiques dans un arbre généalogique sur Ft pnqnet réduction de la fraction d’hétérozygotes autosomiques sur (1-F1) ceux par rapport à une population panmictique.
Mais déjà à travers une génération se rétablit l’équilibre de Hardy – Weinberg qui spécifie la faible importance de l’acte séparé de l’accouplement consanguin pour un arbre généalogique:
 ………(6)
………(6)
Evidemment, pour une population dans son ensemble, l’acte séparé de l’accouplement consanguin aura une importance encore plus faible que pour un arbre généalogique.
Le même effet de variation de la fréquence des génotypes des zygotes est observé et pour les gènes liés au sexe.
La distribution des génotypes liés au chromosome Х dans l’arbre généalogique panmictique est décrite par la loi de Hardy – Weinberg comme 1:
 ………..(7)
………..(7)
La fréquence d’un allèle dominant A on désignera chez les hommes pm et chez les femmes pf. Pour les allèles récessifsa, elle est en conséquence qm et qf .
A l’accouplement, il existe un rapport des génotypes chez les femmes selon le produit (pf + qf) (pm +qm).
Trouvons la probabilité totale d’apparition de l’homozygote récessif aa lors d’un accouplement aléatoire pour les gènes de la fille liés auХ-chromosome selon la formule (2). La logique des événements est similaire à celle des autosomes, sauf que la probabilité conditionnelle de l’apparition d’un génotypeаа à partir des allèles non consanguins selon (7) est égale à P(aa/H1) = qmnqfn. Pour les allèles consanguins, la probabilité conditionnelle de l’apparition d’un génotypeа est égale à P(aa/H2) = qf(n+1). Chez les filles, c’est-à-dire à la génération n+1, la probabilité d’occurrence d’un homozygote aa est déterminée par le fait que si l’allèle a est dans un Х-chromosome, alors à l’origine consanguine de l’homozygote, le même allèle doit nécessairement être et dans le Х-chromosome homologue.
Donc, la probabilité totale d’apparition de l’homozygote récessif est égale :
 ……(8)
……(8)
où pmn est la fréquence des allèles dominants A à la génération n chez les hommes et pfn – chez les femmes. Pour les allèles récessifs a en conséquence qmn et qfn . D’ailleurs on utilise qmn =1 – qmn et pfn = 1 – qfn.
De même trouver la probabilité totale de l’apparition de l’homozygote dominant avec l’utilisation :
 ,
,
 ………..(9)
………..(9)
et un hétérozygote P(Aa) = 1- P(aa) – P(AA) nous trouverons la distribution des génotypes dans les Х-chromosomes de l’arbre généalogique consanguin à l’accouplement :
 ………(10)
………(10)
Il est démontré simultanément qu’aussi bien que dans les autosomes, les additifs consanguins dans les fréquences d’homozygotes dominants et récessifs dans les chromosomes liés au sexe sont identiques.
Une autre façon de trouver le rapport (10) consistera à ce qui suit.
Trouvons d’abord la probabilité totale d’occurrence d’un hétérozygote Aa, c’est-à-dire P(Aa) à l’occasion de l’accouplement consanguin aléatoire. Cette probabilité découle de la logique suivante de l’accouplement : l’origine des allèles est non consanguine (la probabilité de cette hypothèse est P(H1) = 1 – Ft ) survient aussi l’hétérozygote Aа (la probabilité conditionnelle de cet événement est P(Aa/H1) = pmnqfn + pfnqmn, voir la formule (7)) ou l’origine des allèles est consanguine (la probabilité de cette hypothèse est P(H2) = Ft) et il se produit un hétérozygote Aа (la probabilité conditionnelle de cet événement est égale à zéro P(Aa/H2) = 0 ). La dernière affirmation est définie par le fait qu’à l’origine consanguine des allèles similaires dans les Х-chromosomes homologues ne peuvent pas l’hétérozygoteАа surgir constitué d’allèles différents.
Hence, en utilisant la formule de probabilité totale, nous trouvons la probabilité totale de l’occurrence de l’hétérozygote Aa :
 ………(11)
………(11)
La réduction de la fréquence d’un hétérozygote Aa se produit comme cela a été prouvé précédemment en raison de l’augmentation identique de la fréquence des homozygotes dominants AA et récessifs aa. Par exemple, l’augmentation de la fréquence des homozygotes aa récessifs est égale:
 ……..(12)
……..(12)
où la réduction de la fréquence des hétérozygotes Aa par rapport à l’arbre généalogique panmictique selon (7) et (11) est égale. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) En utilisant (11) et (12) pour actualiser (7) pour les cas de consanguinité, nous trouvons la distribution des génotypes (10) dans les Х-chromosomes dans l’arbre généalogique consanguin des filles.
A la génération suivante, la fréquence des allèles récessifs a chez les femmes est égale:
 ……..(13)
……..(13)
Ce qui est tout à fait conforme à la même fréquence en l’absence de consanguinité, c’est-à-dire qu’il y a restauration de l’équilibre Hardy – Weinberg ou plus exactement approche de l’équilibre.
Le rapport (7) et (13) montre dans son ensemble que les fréquences alléliques dans un arbre généalogique pour le compte de la consanguinité ne varient pas. Il y a seulement une redistribution des allèles. Une partie des allèles quittent les hétérozygotes et passent aux homozygotes.
Il s’agit d’une redistribution des allèles.