Retour à l’index des leçons | Faire les leçons dans l’ordre | Page imprimable
Le théorème des facteurs
Le théorème des facteurs est un résultat du théorème du reste, et repose sur le même raisonnement. Si vous n’avez pas lu la leçon sur le théorème du reste, révisez d’abord ce sujet, puis revenez ici.
Comme le souligne le théorème du reste, si vous divisez un polynôme p(x) par un facteur x – a de ce polynôme, alors vous obtiendrez un reste nul. Reprenons cette expression de l’algorithme de division du polynôme :
Avertissement
p(x) = (x – a)q(x) + r(x)
Si x – a est bien un facteur de p(x), alors le reste après division par x – a sera nul. C’est-à-dire :
p(x) = (x – a)q(x)
En termes de Théorème du reste, cela signifie que, si x – a est un facteur de p(x), alors le reste, lorsque nous faisons une division synthétique par
x = a, sera nul.
Le point du Théorème des facteurs est l’inverse du Théorème du reste : Si vous divisez synthétiquement un polynôme par x = a et que vous obtenez un reste nul, alors, non seulement x = a est un zéro du polynôme (courtoisie du Théorème du Reste), mais x – a est aussi un facteur du polynôme (courtoisie du Théorème du Facteur).
Tout comme pour le Théorème du Reste, il ne s’agit pas ici de faire la division longue d’un polynôme donné par un facteur donné. Ce Théorème ne répète pas ce que vous savez déjà, mais essaie plutôt de vous simplifier la vie. Face à un exercice du Théorème des facteurs, vous appliquerez la division synthétique puis vous vérifierez que le reste est nul.
- Utilisez le théorème des facteurs pour déterminer si x – 1 est un facteur de
f (x) = 2×4 + 3×2 – 5x + 7.
Pour que x – 1 soit un facteur de f (x) = 2×4 + 3×2 – 5x + 7, le théorème des facteurs dit que x = 1 doit être un zéro de f (x). Pour vérifier si x – 1 est un facteur, je vais d’abord définir x – 1 égal à zéro et résoudre pour trouver le zéro proposé, x = 1. Ensuite, je vais utiliser la division synthétique pour diviser f (x) par x = 1. Comme il n’y a pas de terme cubique, je prendrai soin de ne pas oublier d’insérer un » 0 » dans la première ligne de la division synthétique pour représenter la puissance omise de x dans 2×4 + 3×2 – 5x + 7 :
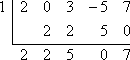
Puisque le reste n’est pas nul, alors le théorème des facteurs dit que :
x – 1 n’est pas un facteur de f (x).
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.
Si x + 4 est un facteur, alors (en mettant ce facteur égal à zéro et en résolvant) x = -4 est une racine. Pour faire la vérification demandée, je dois vérifier que, lorsque j’utilise la division synthétique sur f (x), avec x = -4, j’obtiens un reste nul :
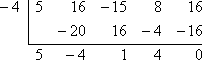
Le reste est nul, donc le théorème des facteurs dit que :
x + 4 est un facteur de 5×4 + 16×3 – 15×2 + 8x + 16.
En pratique, le théorème des facteurs est utilisé lors de la factorisation « complète » de polynômes. Plutôt que d’essayer différents facteurs en utilisant la division longue, vous utiliserez la division synthétique et le théorème des facteurs. Chaque fois que vous divisez par un nombre (étant une racine potentielle du polynôme) et que vous obtenez un reste nul dans la division synthétique, cela signifie que le nombre est effectivement une racine, et donc que « x moins le nombre » est un facteur. Ensuite, vous continuerez la division avec le polynôme plus petit qui en résulte, jusqu’à ce que vous arriviez à un facteur linéaire (vous avez donc trouvé tous les facteurs) ou quadratique (auquel vous pouvez appliquer la formule du quadratique).
- En utilisant le fait que -2 et 1/3 sont des zéros de f (x) = 3×4 + 5×3 + x2 + 5x – 2, factorisez complètement le polynôme. Copyright © Elizabeth Stapel 2002-2011 Tous droits réservés
Si x = -2 est un zéro, alors x + 2 = 0, donc x + 2 est un facteur. De même, si x = 1/3 est un zéro, alors x – 1/3 = 0, donc x – 1/3 est un facteur. En me donnant deux des zéros, ils m’ont aussi donné deux facteurs : x + 2 et x – 1/3.
Puisque j’ai commencé avec un polynôme du quatrième degré, alors je me retrouverai avec un quadratique une fois que j’aurai divisé ces deux facteurs donnés. Je peux résoudre ce quadratique en utilisant la formule du quadratique ou une autre méthode.
Le théorème des facteurs dit que je n’ai pas besoin de faire la division longue avec les facteurs connus de x + 2 et x – 1/3. Au lieu de cela, je peux utiliser la division synthétique avec les zéros associés -2 et 1/3. Voici ce que j’obtiens lorsque je fais la première division avec x = -2 :
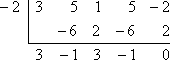
Le reste est nul, ce qui est attendu car on m’avait dit au départ que -2 était un zéro connu du polynôme. Plutôt que de recommencer avec le polynôme d’origine, je vais maintenant travailler sur le facteur polynomial restant de 3×3 – x2 + 3x – 1 (de la ligne inférieure de la division synthétique). Je vais le diviser par l’autre zéro donné, x = 1/3 :
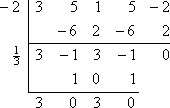
Il me reste donc le quadratique 3×2 + 3, que je peux résoudre :
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Si les zéros sont x = -i et x = i, alors les facteurs sont x – (-i) et x – (i), ou x + i et x – i. I need to remember that I divided off a « 3 » when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. « The Factor Theorem. » Purplemath. Available from 2016
|