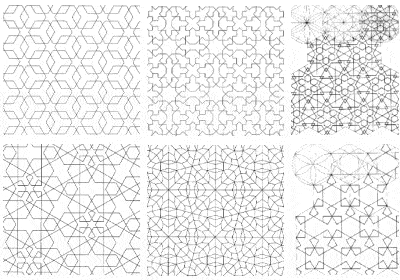
Quelques exemples des symétries complexes utilisées dans la décoration des temples islamiques
L’Empire islamique établi à travers la Perse, le Moyen-Orient, l’Asie centrale, l’Afrique du Nord, l’Ibérie et certaines parties de l’Inde à partir du 8e siècle a apporté des contributions significatives aux mathématiques. Ils ont su s’inspirer des développements mathématiques de la Grèce et de l’Inde et les fusionner.
Une conséquence de l’interdiction islamique de représenter la forme humaine a été l’utilisation extensive de motifs géométriques complexes pour décorer leurs bâtiments, élevant les mathématiques au rang d’art. En effet, au fil du temps, les artistes musulmans ont découvert toutes les différentes formes de symétrie pouvant être représentées sur une surface bidimensionnelle.
Le Coran lui-même encourageait l’accumulation de connaissances, et un âge d’or de la science et des mathématiques islamiques s’est épanoui tout au long de la période médiévale, du IXe au XVe siècle. La Maison de la sagesse a été créée à Bagdad vers 810, et le travail a commencé presque immédiatement pour traduire en arabe les principaux ouvrages de mathématiques et d’astronomie grecs et indiens.
L’exceptionnel mathématicien perse Muhammad Al-Khwarizmi a été l’un des premiers directeurs de la Maison de la sagesse au 9e siècle, et l’un des plus grands des premiers mathématiciens musulmans. La contribution la plus importante d’Al-Khwarizmi aux mathématiques a sans doute été son ardent plaidoyer en faveur du système numérique hindou (1 – 9 et 0), qu’il a reconnu comme ayant la puissance et l’efficacité nécessaires pour révolutionner les mathématiques islamiques (et, plus tard, occidentales), et qui a rapidement été adopté par l’ensemble du monde islamique, puis par l’Europe également.
L’autre contribution importante d’Al-Khwarizmi était l’algèbre, et il a introduit les méthodes algébriques fondamentales de « réduction » et d' »équilibrage » et a fourni un compte rendu exhaustif de la résolution des équations polynomiales jusqu’au second degré. De cette façon, il a contribué à créer le puissant langage mathématique abstrait encore utilisé à travers le monde aujourd’hui, et a permis une façon beaucoup plus générale d’analyser des problèmes autres que les seuls problèmes spécifiques considérés auparavant par les Indiens et les Chinois.
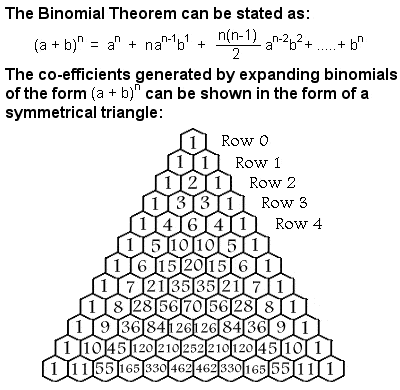
Thorème binomial
Le mathématicien perse du Xe siècle Muhammad Al-Karaji a travaillé à étendre encore plus l’algèbre, en la libérant de son héritage géométrique, et a introduit la théorie du calcul algébrique. Al-Karaji a été le premier à utiliser la méthode de preuve par induction mathématique pour prouver ses résultats, en prouvant que le premier énoncé d’une séquence infinie d’énoncés est vrai, puis en prouvant que, si un énoncé quelconque de la séquence est vrai, alors le suivant l’est aussi.
Théorème binomial
Entre autres choses, Al-Karaji a utilisé l’induction mathématique pour prouver le théorème binomial. Un binôme est un type simple d’expression algébrique qui ne comporte que deux termes sur lesquels on n’opère que par addition, soustraction, multiplication et exposants entiers positifs, comme (x + y)2. Les coefficients nécessaires lorsqu’un binôme est développé forment un triangle symétrique, généralement appelé triangle de Pascal, du nom du mathématicien français du XVIIe siècle Blaise Pascal, bien que de nombreux autres mathématiciens l’aient étudié des siècles avant lui en Inde, en Perse, en Chine et en Italie, notamment Al-Karaji.
Quelques centaines d’années après Al-Karaji, Omar Khayyam (peut-être plus connu comme poète et auteur des « Rubaiyat », mais important mathématicien et astronome à part entière) a généralisé les méthodes indiennes d’extraction des racines carrées et cubiques pour y inclure les racines quatrième, cinquième et supérieures au début du 12e siècle. Il a procédé à une analyse systématique des problèmes cubiques, révélant qu’il existait en fait plusieurs sortes d’équations cubiques différentes. Bien qu’il ait effectivement réussi à résoudre des équations cubiques, et bien qu’on lui attribue généralement le mérite d’avoir identifié les fondements de la géométrie algébrique, il a été freiné dans ses avancées par son incapacité à séparer l’algèbre de la géométrie, et une méthode purement algébrique de résolution des équations cubiques a dû attendre encore 500 ans et les mathématiciens italiens del Ferro et Tartaglia.
Trigonométrie sphérique
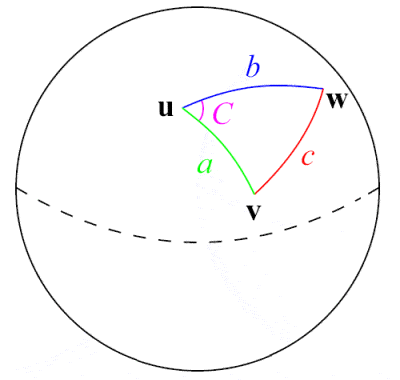
Al-Tusi a été un pionnier dans le domaine de la trigonométrie sphérique
L’astronome, scientifique et mathématicien perse du XIIIe siècle Nasir Al-Din Al-Tusi a peut-être été le premier à traiter la trigonométrie comme une discipline mathématique à part entière, distincte de l’astronomie. S’appuyant sur les travaux antérieurs de mathématiciens grecs tels que Ménélas d’Alexandrie et sur les travaux indiens sur la fonction sinus, il a donné la première exposition détaillée de la trigonométrie sphérique, notamment en énumérant les six cas distincts de triangle rectangle en trigonométrie sphérique. L’une de ses principales contributions mathématiques a été la formulation de la célèbre loi des sinus pour les triangles plans, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), bien que la loi des sinus pour les triangles sphériques ait été découverte plus tôt par les Perses du Xe siècle Abul Wafa Buzjani et Abu Nasr Mansur.
Les autres mathématiciens musulmans médiévaux dignes d’intérêt comprennent :
- l’Arabe du 9ème siècle Thabit ibn Qurra, qui a développé une formule générale par laquelle les nombres amicables pouvaient être dérivés, redécouverts beaucoup plus tard par Fermat et Descartes(les nombres amicables sont des paires de nombres pour lesquels la somme des diviseurs d’un nombre est égale à l’autre nombre, par ex.par exemple, les diviseurs propres de 220 sont 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 et 110, dont la somme est 284 ; et les diviseurs propres de 284 sont 1, 2, 4, 71 et 142, dont la somme est 220) ;
- le mathématicien arabe du 10e siècle Abul Hasan al-Uqlidisi, qui a écrit le plus ancien texte conservé montrant l’utilisation positionnelle des chiffres arabes, et en particulier l’utilisation des décimales au lieu des fractions (par ex.g. 7.375 au lieu de 73⁄8);
- le géomètre arabe du 10e siècle Ibrahim ibn Sinan, qui a poursuivi les investigations d’Archimède sur les aires et les volumes, ainsi que sur les tangentes d’un cercle ;
- le Perse du 11e siècle Ibn al-Haytham (également connu sous le nom d’Alhazen), qui, en plus de ses travaux révolutionnaires sur l’optique et la physique, a établi les débuts du lien entre l’algèbre et la géométrie, et a conçu ce qui est maintenant connu sous le nom de « problème d’Alhazen » (il a été le premier mathématicien à dériver la formule de la somme des puissances quatrièmes, en utilisant une méthode facilement généralisable) ; et
- le Perse du 13e siècle Kamal al-Din al-Farisi, qui a appliqué la théorie des sections coniques pour résoudre des problèmes d’optique, ainsi que la poursuite de travaux en théorie des nombres tels que sur les nombres amicables, la factorisation et les méthodes combinatoires ;
- le Marocain du 13e siècle Ibn al-Banna al-Marrakushi, dont les travaux comprenaient des sujets tels que le calcul des racines carrées et la théorie des fractions continues, ainsi que la découverte de la première nouvelle paire de nombres amicables depuis l’Antiquité (17 296 et 18 416, redécouverts plus tard par Fermat) et la première utilisation de la notation algébrique depuis Brahmagupta.
Avec l’influence étouffante de l’Empire turc ottoman à partir du 14e ou 15e siècle, les mathématiques islamiques ont stagné et les développements ultérieurs se sont déplacés en Europe.
| <<Retour à Madhava | Retour à Al-…Khwarizmi >> |