Avantages de l’utilisation de variables instrumentales pour démontrer la causalité
À titre d’exemple, considérons la question de l’estimation de l’effet de l’éducation sur les gains. La technique d’estimation la plus simple, les moindres carrés ordinaires (MCO), génère des estimations indiquant qu’une année supplémentaire d’éducation est associée à des gains supérieurs de 6 à 10 % . Cependant, la relation positive peut être due à l’auto-sélection vers l’éducation, c’est-à-dire que les individus qui ont le plus à gagner d’une plus grande éducation sont plus susceptibles de rester. Ce sera le cas, par exemple, si les élèves les plus doués trouvent qu’il est plus facile d’étudier, et qu’ils recevraient de toute façon des salaires plus élevés. En tant que telle, la corrélation positive observée entre les années d’études et les salaires refléterait partiellement la prime à la capacité et ne pourrait pas être interprétée comme le rendement d’une année d’études supplémentaire, comme prévu. Les estimations des MCO ne seraient donc pas informatives quant à l’effet d’une politique visant à augmenter le nombre d’années d’études. Ce problème est appelé « biais de variable omise ». Il se produit lorsqu’une variable (telle que la capacité) qui n’est pas observée par le chercheur est corrélée à la fois avec le traitement (plus d’éducation) et avec le résultat (les gains). La direction (surestimation ou sous-estimation) et la taille du biais dans les estimations MCO est fonction du signe et de la force des corrélations.
Dans cet exemple, un essai de contrôle randomisé (ECR), qui impliquerait d’attribuer l’éducation de manière aléatoire aux individus et d’observer les différences de leurs salaires au cours de leur vie, n’est tout simplement pas réalisable pour des raisons éthiques. Cependant, certaines expériences naturelles ou quasi-naturelles peuvent se rapprocher de la modification du choix de l’éducation pour certains groupes d’individus et, à ce titre, peuvent être utilisées comme instruments. L’une de ces expériences naturelles est une modification de l’âge minimum légal auquel les élèves peuvent quitter l’école (âge de fin de scolarité). Ce type de changement affecte tous les élèves, indépendamment de leurs capacités. Il agit donc comme un choc externe qui ne peut pas être influencé par l’élève individuel.
De nombreux pays ont une législation stipulant l’âge auquel les élèves peuvent quitter le système éducatif. Par exemple, disons qu’un enfant peut quitter l’école le dernier jour de l’année scolaire s’il a 14 ans à la fin du mois d’août. Supposons maintenant que la législation soit modifiée, de sorte que les enfants doivent avoir 15 ans à la fin du mois d’août pour être autorisés à quitter l’école. Les enfants qui voulaient quitter l’école à 14 ans en sont empêchés et doivent rester pour une année supplémentaire de scolarité. En partant de l’hypothèse (forte) que les enfants soumis aux deux législations sont similaires et qu’ils sont confrontés à des conditions similaires sur le marché du travail, le changement de législation crée une expérience quasi-naturelle : indépendamment de leurs capacités, certains individus seront affectés par le changement de l’âge de fin de scolarité et devront rester pour une année supplémentaire de scolarité, alors que les élèves de la cohorte précédente ayant des préférences similaires ne le seront pas. Si les chercheurs savaient qui voulait quitter l’école à 14 ans, ils pourraient comparer les résultats des individus qui ont quitté l’école à 14 ans à ceux des individus qui ont été contraints de rester jusqu’à 15 ans. Cette simple différence serait alors l’effet causal du maintien à l’école entre 14 et 15 ans. Malheureusement, les données d’observation ne nous permettent pas d’identifier les individus dont le choix éducatif a été affecté par la réforme ; ainsi, dans le cadre de la nouvelle législation, les individus qui voulaient quitter l’école à 15 ans ne peuvent pas être distingués de ceux qui voulaient quitter l’école à 14 ans mais qui ont dû rester une année de plus. Ce que la réforme fait, néanmoins, c’est modifier la probabilité de rester à l’école, et peut donc être utilisée comme un instrument car elle affecte la probabilité du traitement (une année supplémentaire de scolarité) sans affecter le résultat d’intérêt (par exemple, les revenus).
En 1947, un changement législatif au Royaume-Uni a augmenté l’âge minimum de fin de scolarité de 14 à 15 ans, affectant les enfants nés en 1933 et après. Cette modification de la loi offre l’occasion d’évaluer l’effet de la scolarisation (supplémentaire) sur les gains . Dans le graphique 1, le panel A montre que la réforme a affecté à la fois la fraction d’enfants quittant l’école le plus tôt possible (graphique de gauche) et la quantité totale de scolarité accomplie (graphique de droite). Les estimations indiquent que la réforme a augmenté le nombre moyen d’années de scolarité des hommes de 0,397 année. Cette estimation de l’effet de la réforme (la VI) sur le traitement (l’éducation) est connue sous le nom de « régression de première étape ». Si l’éducation a un effet causal sur les revenus, nous devrions observer que les revenus moyens des individus touchés par la réforme sont également plus élevés. C’est effectivement le cas, comme le montre le panel B de la figure 1, qui rapporte le logarithme des gains moyens des hommes. Cette série présente une rupture nette en 1933, dont l’ampleur implique que les individus touchés par la réforme gagnent, en moyenne, 1,2 % de plus. Cette deuxième estimation de l’effet de la réforme (la VI) sur le résultat (les gains) est connue sous le nom d' »estimation de forme réduite ». Une stratégie IV simple, utilisant dans ce cas un instrument binaire qui ne prend que deux valeurs (1 pour être affecté par la réforme, et 0 pour ne pas être affecté par la réforme), est le rapport de l’estimation de la forme réduite sur l’estimation de la première étape. (Ce ratio est également connu sous le nom d’estimation Wald.) Dans ce cas, l’effet causal de l’éducation supplémentaire sur les revenus serait de 0,012/0,397 = 0,030 et donc d’environ 3%.
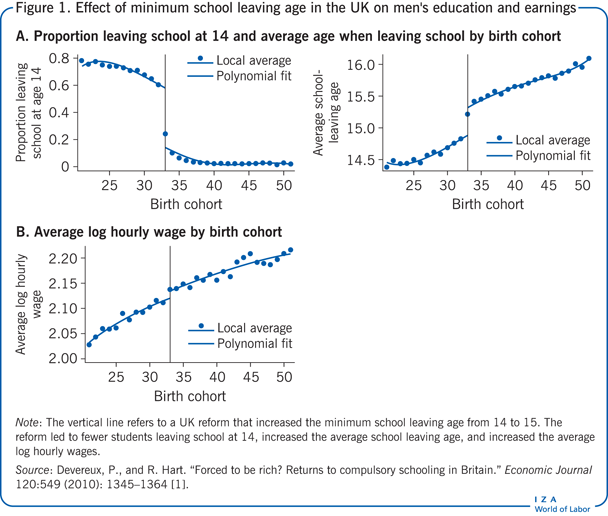
L’intuition de cette approche est que l’effet d’une année d’éducation supplémentaire sur les salaires est fondamentalement l’effet de la réforme (l’IV) sur les salaires (le résultat) – qui est donné dans la forme réduite – mis à l’échelle par l’effet que la réforme a sur les années d’éducation (le traitement) – ce qui est l’objet de l’estimation de première étape. Si l’instrument est « pertinent », c’est-à-dire s’il a un effet sur l’éducation (le traitement), et si l’instrument affecte les salaires « exclusivement » par son effet sur l’éducation, alors les estimations IV peuvent être interprétées comme l’effet causal du traitement sur le résultat. Ces deux conditions sont appelées » pertinence de l’instrument » et » restriction d’exclusion. «
Pour résumer, lorsqu’une variable non observée telle que la capacité est corrélée à la fois avec le traitement et le résultat, une estimation simple comme les MCO sera biaisée en raison de l’auto-sélection dans le traitement. De même, si la variable de traitement est mesurée avec une erreur, l’estimation des MCO sera biaisée vers zéro. Cependant, une estimation causale d’un traitement sur un résultat peut être récupérée si un instrument crédible peut être trouvé. Un instrument crédible doit satisfaire deux conditions :
-
Pertinence : l’instrument doit affecter la probabilité du traitement. Dans une régression du traitement sur l’instrument, également appelée équation de première étape, le coefficient de la VI doit être suffisamment fort.
-
Restriction d’exclusion : l’instrument affecte le résultat exclusivement via son effet sur le traitement.
Si une telle VI peut être trouvée (c’est-à-dire. la pertinence et la restriction d’exclusion sont toutes deux remplies), alors une stratégie IV peut être mise en œuvre pour récupérer un effet causal du traitement sur le résultat.
L’exemple précédent présentait l’estimation de Wald, c’est-à-dire le rapport des estimations de deux régressions : l’estimation de forme réduite, provenant d’une régression du résultat sur l’instrument ; et l’estimation de première étape, provenant d’une régression du traitement sur l’instrument. Ce résultat peut être facilement calculé lorsque l’instrument ne prend que deux valeurs. Dans le cas plus général, une estimation dite « des moindres carrés à deux étapes » (2SLS) sera calculée, les prédictions du traitement provenant de l’équation de première étape étant utilisées dans une régression du résultat sur le traitement, plutôt que la valeur réelle du traitement. Ainsi, seule la variation du traitement provenant de l’instrument est utilisée pour expliquer la variance du résultat. Cela résout donc le biais d’auto-sélection. Dans le cas d’un instrument binaire (à deux valeurs), les estimations Wald et 2SLS seront identiques (voir , par exemple). Cependant, la difficulté ne réside pas dans la mise en œuvre d’une telle estimation 2SLS, tous les progiciels statistiques peuvent calculer des estimations IV, mais dans (a) la recherche d’un instrument valide et (b) l’interprétation des résultats. La discussion va maintenant se concentrer sur ces deux points.
.