Vissza a leckék indexéhez | A leckék sorrendje | Nyomtatható oldal
A tényezőtétel
A tényezőtétel a maradéktétel eredménye, és ugyanazon az érvelésen alapul. Ha még nem olvastad el a maradéktételről szóló leckét, először azt a témakört nézd át, majd térj vissza ide.
Amint a maradéktétel rámutat, ha egy p(x) polinomot elosztasz a polinom x – a tényezőjével, akkor nulla maradékot kapsz. Nézzük meg újra a polinomnak ezt az osztási algoritmus szerinti kifejezését:
Hirdetés
- (x) = (x – a)q(x) + r(x)
Ha x – a valóban p(x) tényezője, akkor az x – a-val való osztás utáni maradék nulla lesz. Vagyis:
- (x) = (x – a)q(x)
A maradéktétel szempontjából ez azt jelenti, hogy ha x – a p(x) tényezője, akkor a maradék, amikor szintetikus osztást végzünk
x = a-val, nulla lesz.
A faktor-tétel lényege a maradéktétel fordítottja: Ha egy polinomot szintetikusan osztunk x = a-val, és nulla maradékot kapunk, akkor nem csak az x = a a polinom nullája (a maradéktétel jóvoltából), hanem az x – a is a polinom tényezője (a tényezőtétel jóvoltából).
Mint a maradéktétel esetében, itt sem az a lényeg, hogy egy adott polinomnak egy adott tényezővel való hosszú osztását végezzük el. Ez a tétel nem azt ismétli, amit már tudsz, hanem megpróbálja egyszerűbbé tenni az életedet. Amikor egy tényezőtételes feladattal szembesülsz, szintetikus osztást fogsz alkalmazni, majd ellenőrizni fogod, hogy van-e nulla maradék.
- A Faktor-tétel segítségével határozd meg, hogy x – 1 tényezője-e
f (x) = 2×4 + 3×2 – 5x + 7.
Hogy x – 1 tényezője legyen f (x) = 2×4 + 3×2 – 5x + 7-nek, a Faktor-tétel szerint x = 1 az f (x) nullájának kell lennie. Ahhoz, hogy megvizsgáljam, hogy x – 1 faktor-e, először x – 1-t nullával teszem egyenlővé, és megoldom, hogy megtaláljam a javasolt nullát, x = 1-et. Ezután szintetikus osztás segítségével elosztom f (x) x = 1-gyel. Mivel nincs köbös tag, ügyelni fogok arra, hogy ne felejtsek el egy “0”-t beilleszteni a szintetikus osztás első sorába, hogy a 2×4 + 3×2 – 5x + 7-ben az x kihagyott hatványát jelképezze:
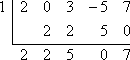
Mivel a maradék nem nulla, akkor a tényezőtétel szerint:
x – 1 nem f (x) tényezője.
- A Faktor-tétel segítségével ellenőrizd, hogy x + 4 a
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16 tényezője.
Ha x + 4 tényező, akkor (ezt a tényezőt nullával egyenlővé téve és megoldva) x = -4 gyök. A szükséges ellenőrzéshez ellenőriznem kell, hogy ha szintetikus osztást alkalmazok f(x)-en, x = -4-gyel, akkor nulla maradékot kapok:
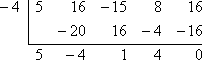
A maradék nulla, tehát a Faktor-tétel szerint:
x + 4 az 5×4 + 16×3 – 15×2 + 8x + 16 tényezője.
A gyakorlatban a faktortételt a polinomok “teljes” faktorálásakor használjuk. Ahelyett, hogy a különböző faktorokat hosszú osztással próbálnánk ki, inkább a szintetikus osztást és a Faktor-tételt használjuk. Bármikor, amikor osztasz egy számmal (ami a polinom potenciális gyöke), és a szintetikus osztásnál nulla maradékot kapsz, ez azt jelenti, hogy a szám valóban gyök, és így “x mínusz a szám” egy faktor. Ezután az így kapott kisebb polinommal folytatod az osztást, egészen addig, amíg lineáris tényezőhöz (tehát az összes tényezőt megtaláltad) vagy kvadratikushoz (amire a kvadratikus képletet alkalmazhatod) nem jutsz.
- Azt a tényt felhasználva, hogy -2 és 1/3 az f (x) = 3×4 + 5×3 + x2 + 5x – 2 zérusai, teljesen faktoráld a polinomot. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
Ha x = -2 nulla, akkor x + 2 = 0, tehát x + 2 egy tényező. Hasonlóképpen, ha x = 1/3 egy nulla, akkor x – 1/3 = 0, tehát x – 1/3 egy tényező. Azzal, hogy két nullát adtak meg, két faktort is adtak: x + 2 és x – 1/3.
Miután egy negyedfokú polinommal kezdtem, akkor egy kvadratikus marad, ha ezt a két adott faktort kiosztom. Ezt a kvadratikust a kvadratikus képlet vagy más módszer segítségével tudom megoldani.
A tényezőtétel szerint nem kell hosszú osztást végeznem az x + 2 és x – 1/3 ismert tényezőivel. Ehelyett használhatom a szintetikus osztást a hozzá tartozó -2 és 1/3 nullákkal. A következőt kapom, ha az első osztást x = -2-vel végzem:
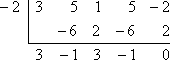
A maradék nulla, ami várható volt, mert az elején azt mondták, hogy -2 a polinom ismert nullája. Ahelyett, hogy újra kezdeném az eredeti polinommal, most a 3×3 – x2 + 3x – 1 (a szintetikus osztás alsó sorából) maradék polinomtényezőjével fogok dolgozni. Ezt fogom osztani a másik adott nullával, x = 1/3:
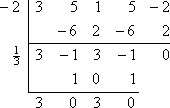
Megmarad a 3×2 + 3 kvadrát, amit meg tudok oldani:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Ha a nullpontok x = -i és x = i, akkor a tényezők x – (-i) és x – (i), vagy x + i és x – i lesznek. I need to remember that I divided off a “3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. “The Factor Theorem.” Purplemath. Available from 2016
|