Az instrumentális változók használatának előnyei a kauzalitás bizonyítására
Példaként tekintsük az oktatás keresetre gyakorolt hatásának becslését. A legegyszerűbb becslési technika, a legkisebb négyzetek (ordinary least squares, OLS) olyan becsléseket eredményez, amelyek azt mutatják, hogy egy plusz egy év oktatás 6-10%-kal magasabb keresettel jár. A pozitív kapcsolat mögött azonban az oktatásba való önszelekció állhat, azaz azok az egyének, akik a legtöbbet nyerhetnek a magasabb iskolai végzettséggel, nagyobb valószínűséggel maradnak. Ez a helyzet például akkor áll fenn, ha a jobb képességű tanulóknak könnyebb a tanulás, és valószínűleg egyébként is magasabb béreket kapnának. Így az oktatási évek és a bérek között megfigyelt pozitív korreláció részben a képességek prémiumát tükrözné, és nem úgy értelmezhető, mint egy további oktatási év hozadéka, ahogyan az szándékolt. Az OLS-becslések így nem lennének informatívak az oktatási évek növelését célzó politika hatásáról. Ezt a problémát “kihagyott változó torzításnak” nevezik. Ez akkor fordul elő, ha egy olyan változó (például a képesség), amelyet a kutató nem figyel meg, korrelál mind a kezeléssel (több oktatás), mind a kimenettel (kereset). Az OLS-becslések torzításának iránya (túl- vagy alulbecslés) és mértéke a korrelációk előjelének és erősségének függvénye.
Ebben a példában a randomizált kontrollvizsgálat (RCT), amely azt jelentené, hogy az egyéneket véletlenszerűen osztanák el az oktatásban, és megfigyelnék a bérekben az életük során mutatkozó különbségeket, etikai okokból egyszerűen nem kivitelezhető. Néhány természetes vagy kvázi-természetes kísérlet azonban közel kerülhet ahhoz, hogy az egyének bizonyos csoportjai számára megváltoztassa az oktatási választást, és mint ilyenek, eszközként használhatók. Az egyik ilyen természetes kísérlet az iskolából való kilépés törvényes alsó korhatárának (iskolaelhagyási korhatár) megváltoztatása. Ez a fajta változás minden tanulót érint, képességeiktől függetlenül. Ezért úgy hat, mint egy külső sokk, amelyet az egyes tanulók nem tudnak befolyásolni.
Néhány országban van olyan jogszabály, amely meghatározza azt az életkort, amelyben a tanulók elhagyhatják az oktatási rendszert. Mondjuk például, hogy egy gyermek a tanév utolsó napján elhagyhatja az iskolát, ha augusztus végére betölti a 14. életévét. Tegyük most fel, hogy a jogszabályokat úgy módosítják, hogy a gyermekeknek augusztus végéig 15 évesnek kell lenniük ahhoz, hogy elhagyhassák az iskolát. Azok a gyerekek, akik 14 évesen el akarták hagyni az iskolát, nem tehetik ezt meg, és további egy évet kell maradniuk az iskolában. Azzal az (erős) feltételezéssel, hogy a két jogszabály hatálya alá tartozó gyermekek hasonlóak, és hasonló munkaerő-piaci feltételekkel szembesülnek, a jogszabályi változás kvázi természetes kísérletet hoz létre: képességeiktől függetlenül néhány személyt érint az iskolaelhagyási korhatár változása, és további egy évet kell maradniuk az iskolában, míg a korábbi kohorszból származó, hasonló preferenciákkal rendelkező tanulók nem. Ha a kutatók tudnák, hogy ki akarta 14 évesen elhagyni az iskolát, akkor össze tudnák hasonlítani a 14 évesen iskolát elhagyó egyének eredményeit azokéval, akiknek 15 éves korukig kellett maradniuk. Ez az egyszerű különbség lenne az iskolában maradás okozati hatása 14 és 15 éves kor között. Sajnos a megfigyelési adatok nem teszik lehetővé, hogy azonosítsuk azokat az egyéneket, akiknek az oktatási választását a reform befolyásolta; így az új jogszabályok értelmében azok az egyének, akik 15 évesen akarták elhagyni az iskolát, megkülönböztethetetlenek azoktól, akik 14 évesen akarták elhagyni, de még egy évig maradniuk kellett. A reform mindazonáltal megváltoztatja az iskolában maradás valószínűségét, és így eszközként használható, mivel a kezelés valószínűségét (még egy év iskolába járás) befolyásolja, anélkül, hogy az érdekeltségi eredményt (pl. a jövedelmet) befolyásolná.
Az Egyesült Királyságban 1947-ben egy törvénymódosítás 14-ről 15 évre emelte a minimális iskolai végzettségi kort, ami az 1933-ban és azután született gyermekeket érintette. Ez a törvénymódosítás lehetőséget nyújt arra, hogy értékeljük a (további) iskolai végzettségnek a keresetre gyakorolt hatását. Az 1. ábra A. panelje azt mutatja, hogy a reform mind az iskolát a lehető legkorábban elhagyó gyermekek arányára (bal oldali ábra), mind a teljes iskolai végzettségre (jobb oldali ábra) hatással volt. A becslések azt mutatják, hogy a reform 0,397 évvel növelte a férfiak átlagos iskolázottsági éveit. A reformnak a kezelésre (oktatás) gyakorolt hatásának (az IV) ezt a becslését “első lépcsős regressziónak” nevezzük. Ha az oktatásnak van valamilyen ok-okozati hatása a keresetekre, akkor azt kellene megfigyelnünk, hogy a reform által érintett egyének átlagkeresete is magasabb. Ez valóban így van, amint azt az 1. ábra B panelje mutatja, amely a férfiak átlagos logaritmikus keresetét mutatja. Ez a sorozat egyértelmű törést mutat 1933-ban, amelynek nagyságrendje azt jelenti, hogy a reform által érintett egyének átlagosan 1,2%-kal magasabb bért keresnek. A reformnak a kimenetelre (kereset) gyakorolt hatásának (IV) ezt a második becslését “csökkentett formájú becslésnek” nevezzük. Egy egyszerű IV-stratégia, amely ebben az esetben egy olyan bináris instrumentumot használ, amely csak két értéket vesz fel (1, ha a reform hatással van rá, és 0, ha nem érinti a reform), a csökkentett formájú becslés és az első szakaszbeli becslés hányadosa. (Ezt az arányt Wald-becslésnek is nevezik.) Ebben az esetben a többletképzés keresetre gyakorolt oksági hatása 0,012/0,397 = 0,030, tehát körülbelül 3% lenne.
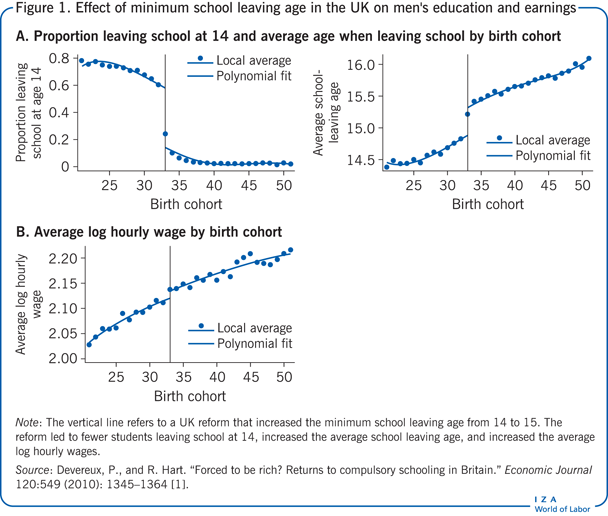
A megközelítés intuíciója az, hogy az egy évvel több iskolai végzettség hatása a bérekre alapvetően a reform (az IV) hatása a bérekre (az eredményre) – ami a csökkentett formában adott -, felskálázva a reformnak az iskolai évekre (a kezelésre) gyakorolt hatásával – amiről az első lépcsős becslés szól. Ha az eszköz “releváns”, azaz hatással van az oktatásra (a kezelésre), és ha az eszköz “kizárólag” az oktatásra gyakorolt hatásán keresztül befolyásolja a béreket, akkor az IV becslések a kezelésnek az eredményre gyakorolt oksági hatásaként értelmezhetők. Ezt a két feltételt “instrumentum relevanciának” és “kizárási korlátozásnak” nevezzük.”
Összefoglalva, ha egy nem megfigyelt változó, mint például a képesség, mind a kezeléssel, mind a kimenettel korrelál, akkor egy egyszerű becslés, mint például az OLS, torzított lesz a kezelésbe való önszelekció miatt. Hasonlóképpen, ha a kezelési változót hibásan mérik, az OLS-becslés nulla felé torzul. A kezelésnek a kimenetelre gyakorolt oksági becslése azonban helyreállítható, ha hiteles instrumentumot találunk. A hiteles instrumentumnak két feltételnek kell megfelelnie:
-
Relevancia: az instrumentumnak ki kell hatnia a kezelés valószínűségére. A kezelésnek az instrumentumra való regressziójában, amelyet első lépcsős egyenletnek is neveznek, az IV együtthatójának kellően erősnek kell lennie.
-
Kizárási korlátozás: az instrumentum kizárólag a kezelésre gyakorolt hatásán keresztül befolyásolja a kimenetelt.
Ha egy ilyen IV megtalálható (azaz. mind a relevancia-, mind a kizárási korlátozás teljesül), akkor egy IV-stratégiát lehet alkalmazni a kezelés kimenetelre gyakorolt oksági hatásának helyreállítására.
Az előző példában bemutattuk a Wald-becslést, azaz a két regresszióból származó becslések arányát: a redukált formájú becslést, amely a kimenetelnek az eszközre való regressziójából származik; és az első lépcsős becslést, amely a kezelésnek az eszközre való regressziójából származik. Ez könnyen kiszámítható, ha az eszköz csak két értéket vesz fel. Általánosabb esetben egy úgynevezett “kétlépcsős legkisebb négyzetek” (2SLS) becslést kell kiszámítani, ahol a kezelés első lépcsős egyenletből származó előrejelzéseit használják a kezelés valódi értéke helyett az eredménynek a kezelésre történő regressziójában. Így csak a kezelésnek az eszközből származó változékonyságát használják fel a kimenetel varianciájának magyarázatára. Ez megoldja az önszelekciós torzítást. Bináris (kétértékű) instrumentum esetén a Wald- és a 2SLS-becslések azonosak lesznek (lásd például az alábbi példát). A nehézség azonban nem az ilyen 2SLS becslés végrehajtásában rejlik, minden statisztikai csomag képes IV becslések kiszámítására, hanem a) az érvényes instrumentum megtalálásában és b) az eredmények értelmezésében. A vita most erre a két pontra fog összpontosítani.