Léteznek olyan családfák és populációk, ahol a pánmiktikus párosodás elve lényegében megszakad. Általában földrajzilag vagy társadalmilag viszonylag elszigetelt kis közösségekről van szó. Ezekben a közösségekben a beltenyésztés, azaz a különböző rendű vérrokonsági párosodás (szülő – gyermek, testvérek, unokatestvérek, nagybácsi – unokahúg stb.) széles körben elterjedt lehet.
A beltenyészetnek a populációra gyakorolt hatásának problémája a genetika fontos problémája1. Most ez a probléma még nem kapott végleges megoldást.
A legtöbb esetben a beltenyésztést egy családfán három generáción keresztül vesszük figyelembe. Ez a legtávolabbi rokonok, akiket figyelembe vesznek a vérszerinti párosodásnál vannak másod-unokatestvérek.
A beltenyésztést a beltenyésztési tényező segítségével vesszük figyelembe.
A beltenyésztési tényező az a valószínűség, hogy két allél származás szerint azonos.
Megvizsgáljuk a Wright 1, 2 által kínált módszert a beltenyésztési tényező kiszámítására egy családfán.
A beltenyésztési tényező megtalálásához szükséges:
meg kell találni a házasodó leszármazottak számára a családfán minden olyan utat, amely a közös ősön keresztül összeköti ezeket a leszármazottakat.
Az egyes utakon a lépések (generációk váltakozásai) számát kell megszámolni.
Ezután a beltenyésztési tényező egyenlő:
 ……(1)
……(1)
ahol r az utak száma, m1, m2, … mi- lépések száma az egyes utakon.
Még egyszer megjegyezzük, hogy az (1) összegben az összeadódások száma megegyezik azon utak számával, amelyek a közös ősökön keresztül összekötik a házasságot.
Megnézzük a családfák konkrét eseteit, az 1. ábrát. Ezen az ábrán a négyzet férfi egyedet jelent a kör – női egyedet. A szaggatott vonalak és az azonos számjegyek a családfán belüli lehetséges utakat adják meg, amelyek a közös ősökön (a férfin vagy a nőn) keresztül a leszármazottak vérszerinti házasságot kötnek. Az utak egyes oldalain (1. ábra) az 1. és 2. számjegyek szerepelnek. Ez azt jelzi, hogy az ilyen helyek a különböző utak közösek.
Az apa – lánya házassága vérfertőzés, 1. ábra. A leszármazott (nő) az ottani őshöz (férfi) 1 úton kapcsolódik egy lépéssel, azaz m = 1. Tehát van beltenyésztési tényező.
Ft = 1/2,2-1 = 1/4
A házasság egy testvér – testvér (sibs), 1b. ábra. A számjegyek az út számát adják meg. Az azonos számjegyek száma az úton a házasodó férfitól a nőig megegyezik a lépések számával.
Mindegyik leszármazott, aki házasodott, két úton kapcsolódik a partneréhez, mindkét úton két lépéssel, azaz m = 2. Tehát van beltenyésztési tényező.
Ft = 1/2.(2-2 + 2-2) = 1/4
Az unokatestvérek közötti házasság az 1. ábrán látható.
1. ábra. A beltenyésztés néhány fajtája egy családfán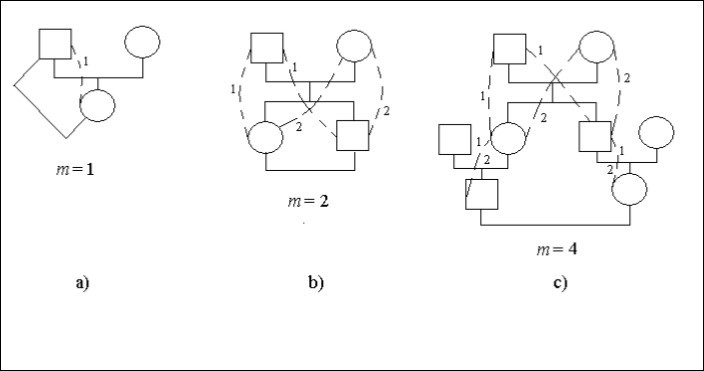
Minden leszármazott, aki házasságot kötött a partnerével a 2 úton 4 lépéssel kapcsolódik az egyes utakon, azaz m = 4. Tehát van beltenyésztési tényező.
Ft = 1/2.(2-4 + 2-4) = 1/16
A (1) képletet a következő logika alapján könnyű megérteni.
A gyermek génjei nyilvánvalóan 1/2 közös minden szülővel, 1/4 – a nagyapával és a nagymamával, 1/8 – a dédapával és a dédnagyanyával stb. Ha a nőtől bármelyik őshöz η lépéssel vezet az út, akkor a közös gének aránya ezzel az őssel egyenlő 2-η. Ha a férfi bármelyik ősétől μ lépésekkel vezet az út, akkor a közös gének aránya 2-μ. A férfi és a nő házasságakor a közös őssel a közös gének aránya ezzel az őssel 2-η lesz. 2-μ = 2-m, ahol m = η + μ a közös ősön keresztül a nőtől a férfi házasságáig tartó lépések teljes száma. Az 1/2 2-m nagysága annak a valószínűségét mutatja, hogy a nőnél véletlenül kiválasztott gén eredetét tekintve azonos lesz a férfinál véletlenül kiválasztott génnel. Ugyanez a méret adja meg a beltenyésztési tényezőhöz való hozzájárulást Ft egy úton keresztül a közös ősön keresztül a nőtől a férfi házasodásáig.
Ha például a közös ős a házasságkötéstől η = μ = 5 generáción keresztül távol lesz, akkor annak valószínűsége, hogy a közös génnel rendelkeznek, egyenlő. 1/2 2-(5+5) = 1/2048 Ez a méret a párosodás elemzésénél elhanyagolható. (1. táblázat)
Az 1. táblázatban az egyes vérrokonsági házasságok beltenyésztési tényezőit mutatjuk be.
| A vérrokonsági fajták típusa. házasság | Beltenyésztési tényező Ft |
| Másodfokú unokatestvérek | 1/32 |
| Unokatestvér nagybácsi – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: az azonos allélok eredete a homológ autoszómákban nem konzangvinikus (ennek a hipotézisnek a valószínűsége P(H1) = 1- Ft )egyben homozigótaаа is keletkezik (ennek az eseménynek a feltételes valószínűsége P(aa/H1) = q2) vagy az azonos allélok eredete konzangvinikus (ennek a hipotézisnek a valószínűsége P(H2) = Ft ) és homozigótaаа keletkezik (ennek az eseménynek a feltételes valószínűsége P(aa/H2) = q). Az aa homozigóta előfordulásának q valószínűségét az utóbbi esetben az határozza meg, hogy ha az a allél az egyik autoszómában van, akkor a homozigóta konzangvinikus eredeténél ugyanannak az allélnak szükségszerűen és a homológ autoszómában kell lennie.
Ezért a recesszív homozigóta előfordulásának teljes valószínűsége egyenlő:
 ……….(3)
……….(3)
ahol figyelembe vesszük p = 1 – q van a domináns allél a gyakorisága.
Hasonlóképpen ott találjuk a domináns homozigóta AA előfordulásának teljes valószínűségét véletlenszerű párosítás esetén:
 ……….. (4)
……….. (4)
A (3) és (4) szerint tehát a beltenyésztett családfán a homozigóták (domináns és recesszív) teljes gyakorisága 2Ftpq-ra nő. Ezért a heterozigóták gyakorisága azonos méret esetén csökken, és egyenlő lesz 2pq – 2pqFt = 2pq(1-Ft), mivel az összes zigótafrekvencia összege egyenlő 1-gyel.
A beltenyésztési tényező, valamint (3) és (4) figyelembevételével a Hardy – Weinberg törvényt egy autoszomális genomra vonatkozó beltenyésztett családfa következő generációjában a zigóta genotípusok eloszlásait 4-re kell felírni:
 …………(5)
…………(5)
Ahol pn a domináns allél A gyakorisága az n generációban, qn – a recesszív allél a gyakorisága, tehát pn + qn = 1.
A (5) arányszám utal a Wright-arányszámra is 5. A Wright-arányszám azt mutatja, hogy egy beltenyésztett családfában az egyedek vérszerinti párosítása után a következő hatások figyelhetők meg: egy családfában pnqn Ft-on nő az autoszomális homozigóta frakció, és csökken az autoszomális heterozigóta frakció az (1-F1)-ekben egy pánmiktikus populációhoz képest.
De már egy generáción keresztül helyreáll a Hardy – Weinberg egyensúly, ami meghatározza a különálló vérrokonsági párosodás kis jelentőségét egy családfa számára:
 ………(6)
………(6)
Nyilvánvaló, hogy egy populáció egésze számára a különálló vérrokonsági párosodásnak még kisebb jelentősége lesz, mint egy családfa számára.
A zigóta genotípusok gyakoriságának variációjának ugyanez a hatása figyelhető meg és a nemhez kötött gének esetében is.
A Х-kromoszómához kötött genotípusok eloszlását a pánmiktikus családfában a Hardy – Weinberg-törvény a következőképpen írja le: 1:
 ………..(7)
………..(7)
A domináns A allél gyakoriságát a férfiaknál pm, a nőknél pf jelöljük. A recesszív allélesa esetében ennek megfelelően qm és qf .
Párosodáskor a nőknél a genotípusok aránya a (pf + qf) (pm +qm) szorzatának megfelelően alakul.
Megkeressük az aa recesszív homozigóta előfordulásának teljes valószínűségét véletlenszerű párosításkor a lányoknak aХ-kromoszómához kötött génjeihez a (2) képlet alapján. Az események logikája hasonló, mint az autoszómák esetében, azzal a különbséggel, hogy a (7) szerint a nem-konzangvinikus allélokból származó genotípusаа előfordulásának feltételes valószínűsége egyenlő P(aa/H1) = qmnqfn. A vérrokonsági allélok esetében a genotípusаа előfordulásának feltételes valószínűsége egyenlő P(aa/H2) = qf(n+1). A leányoknál, azaz az n+1 generációban az aa homozigóta előfordulásának valószínűségét az határozza meg, hogy ha az a allél az egyik Х-kromoszómában van, akkor a homozigóta vérszerinti eredeténél ugyanannak az allélnak szükségszerűen a homológ Х-kromoszómában kell lennie.
Ezért a recesszív homozigóta előfordulásának teljes valószínűsége egyenlő:
 ……(8)
……(8)
ahol pmn a domináns allél A gyakorisága az n generációban a férfiaknál és pfn – a nőknél. A recesszív allélok a ennek megfelelően qmn és qfn . Emellett qmn =1 – qmn és pfn = 1 – qfn.
Hasonlóan a domináns homozigóta előfordulásának teljes valószínűségének megállapításához használjuk:
 ,
,
 ………..(9)
………..(9)
és egy heterozigóta P(Aa) = 1- P(aa) – P(AA) a beltenyésztett családfa Х-kromoszómáiban a genotípusok eloszlását találjuk párosításkor:
 ………(10)
………(10)
Ezzel egyidejűleg kimutatható, hogy az autoszómákhoz hasonlóan a beltenyésztett adalékok a domináns és recesszív homozigóta gyakoriságokban a nemhez kötött kromoszómákban is azonosak.
A (10) arány megállapításának másik módja a következőkben áll.
Lássuk először az Aa heterozigóta előfordulásának teljes valószínűségét, azaz P(Aa) a véletlenszerű vérrokonsági párosítás alkalmával. Ez a valószínűség a következő párosodási logikából következik: az allélok eredete nem vérrokon (ennek a hipotézisnek a valószínűsége P(H1) = 1 – Ft ) létrejön a heterozigóta Aa is (ennek az eseménynek a feltételes valószínűsége P(Aa/H1) = pmnqfn + pfnqmn, lásd a (7) képletet) vagy az allélok eredete vérszerinti (ennek a hipotézisnek a valószínűsége P(H2) = Ft) és heterozigóta Aа keletkezik (ennek az eseménynek a feltételes valószínűsége nulla P(Aa/H2) = 0 ). Az utolsó állítást az határozza meg, hogy vérségi eredet esetén a homológ Х-kromoszómákban lévő hasonló alléloknál nem keletkezhet a heterozigóta Aa különböző allélokból álló heterozigóta.
Az összvalószínűség képletét felhasználva tehát a heterozigóta Aa előfordulásának összvalószínűségét találjuk:
 ……..(11)
……..(11)
A heterozigóta Aa gyakoriságának csökkenése a korábban bizonyított módon a domináns AA és a recesszív aa homozigóta gyakoriságának azonos mértékű növekedése miatt következik be. Például a recesszív aa homozigóta gyakoriság növekedése egyenlő:
 ……..(12)
……..(12)
mivel a heterozigóta Aa gyakoriság csökkenése a (7) és (11) szerinti pánmiktikus családfához képest egyenlő. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) (11) és (12) felhasználásával a (7) frissítésével a beltenyésztés eseteire vonatkozóan megtaláljuk a genotípusok (10) eloszlását a Х-kromoszómákban a leányok beltenyésztett családfáján.
A következő generációban a recesszív allélok gyakorisága a nőknél egyenlő:
 ……..(13)
……..(13)
Ez teljesen megfelel a beltenyésztés hiányában azonos gyakoriságnak, azaz helyreáll a Hardy – Weinberg egyensúly, vagy pontosabban megközelíti az egyensúlyt.
A (7) és (13) arányszámok összességében azt mutatják, hogy az allélfrekvenciák a családfán a beltenyésztés figyelembevételével nem változnak. Csak allélátrendeződés van. Az allélok egy része elhagyja a heterozigótákat és átkerül a homozigótákhoz.