Il Teorema del Fattore

Come sottolinea il Teorema del Rimanente, se si divide un polinomio p(x) per un fattore x – a di quel polinomio, allora si ottiene un resto nullo. Guardiamo di nuovo l’espressione dell’algoritmo di divisione del polinomio:

p(x) = (x – a)q(x) + r(x)

Se x – a è effettivamente un fattore di p(x), allora il resto dopo la divisione per x – a sarà zero. Cioè:

p(x) = (x – a)q(x)

In termini di Teorema del resto, questo significa che, se x – a è un fattore di p(x), allora il resto, quando facciamo la divisione sintetica per
x = a, sarà zero: Se dividi sinteticamente un polinomio per x = a e ottieni un resto zero, allora, non solo x = a è uno zero del polinomio (per gentile concessione del Teorema del resto), ma x – a è anche un fattore del polinomio (per gentile concessione del Teorema del fattore).

Proprio come per il Teorema del resto, il punto qui non è fare la divisione lunga di un dato polinomio per un dato fattore. Questo Teorema non sta ripetendo ciò che già sapete, ma sta invece cercando di rendervi la vita più semplice. Quando affronterete un esercizio del Teorema dei Fattori, applicherete la divisione sintetica e poi controllerete che il resto sia zero.

• Usa il Teorema dei Fattori per determinare se x – 1 è un fattore di
  f (x) = 2×4 + 3×2 – 5x + 7.

Perché x – 1 sia un fattore di f (x) = 2×4 + 3×2 – 5x + 7, il Teorema dei Fattori dice che x = 1 deve essere uno zero di f (x). Per testare se x – 1 è un fattore, prima porrò x – 1 uguale a zero e risolverò per trovare lo zero proposto, x = 1. Poi userò la divisione sintetica per dividere f (x) per x = 1. Poiché non c’è un termine al cubo, farò attenzione a ricordare di inserire uno “0” nella prima riga della divisione sintetica per rappresentare la potenza omessa di x in 2×4 + 3×2 – 5x + 7:

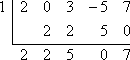
Siccome il resto non è zero, allora il teorema dei fattori dice che:

x – 1 non è un fattore di f (x).

• Utilizzando il Teorema dei Fattori, verifica che x + 4 è un fattore di
  f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.

Se x + 4 è un fattore, allora (mettendo questo fattore uguale a zero e risolvendo) x = -4 è una radice. Per fare la verifica richiesta, devo controllare che, quando uso la divisione sintetica su f (x), con x = -4, ottengo un resto nullo:

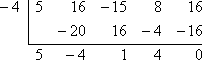
Il resto è zero, quindi il teorema dei fattori dice che:

x + 4 è un fattore di 5×4 + 16×3 – 15×2 + 8x + 16.

In pratica, il Teorema del Fattore viene usato quando si fattorizzano polinomi “completamente”. Piuttosto che provare i vari fattori usando la divisione lunga, si usa la divisione sintetica e il Teorema del Fattore. Ogni volta che si divide per un numero (essendo una potenziale radice del polinomio) e si ottiene un resto zero nella divisione sintetica, questo significa che il numero è effettivamente una radice, e quindi “x meno il numero” è un fattore. Poi continuerai la divisione con il polinomio più piccolo risultante, continuando fino ad arrivare ad un fattore lineare (quindi hai trovato tutti i fattori) o un quadratico (al quale puoi applicare la Formula Quadratica).

• Usando il fatto che -2 e 1/3 sono zeri di f (x) = 3×4 + 5×3 + x2 + 5x – 2, fattorizza completamente il polinomio. Copyright © Elizabeth Stapel 2002-2011 Tutti i diritti riservati

Se x = -2 è uno zero, allora x + 2 = 0, quindi x + 2 è un fattore. Allo stesso modo, se x = 1/3 è uno zero, allora x – 1/3 = 0, quindi x – 1/3 è un fattore. Dandomi due zeri, mi hanno dato anche due fattori: x + 2 e x – 1/3.

Siccome ho iniziato con un polinomio di quarto grado, allora mi ritroverò con una quadratica una volta divisi questi due fattori dati. Posso risolvere quella quadratica usando la Formula Quadratica o qualche altro metodo.

Il Teorema dei Fattori dice che non devo fare la divisione lunga con i fattori noti di x + 2 e x – 1/3. Invece, posso usare la divisione sintetica con gli zeri associati -2 e 1/3. Ecco cosa ottengo quando faccio la prima divisione con x = -2:

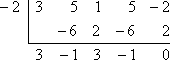
Il resto è zero, che è previsto perché mi avevano detto all’inizio che -2 era uno zero noto del polinomio. Invece di ricominciare da capo con il polinomio originale, ora lavorerò sul fattore polinomiale rimanente di 3×3 – x2 + 3x – 1 (dalla linea inferiore della divisione sintetica). Lo dividerò per l’altro zero dato, x = 1/3:

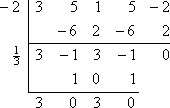
Questo mi lascia con la quadratica 3×2 + 3, che posso risolvere:

3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i

Se gli zeri sono x = -i e x = i, allora i fattori sono x – (-i) e x – (i), o x + i e x – i. I need to remember that I divided off a “3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:

3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)

Top | Return to Index