Ci sono alberi genealogici e popolazioni dove il principio di accoppiamento panmico è essenzialmente rotto. Di solito si tratta di piccole comunità geograficamente o socialmente relativamente isolate. In queste comunità l’inbreeding, cioè l’accoppiamento consanguineo di vari ordini (un genitore – un figlio, fratelli, cugini, zio – nipote, ecc.), può essere molto diffuso.
Il problema dell’influenza dell’inbreeding sulla popolazione è il problema importante della genetica 1. Ora questo problema non ha ancora ricevuto la soluzione definitiva.
Nella maggior parte dei casi l’inbreeding in un albero genealogico tiene conto di tre generazioni. Sono i parenti più lontani che sono presi in considerazione all’accoppiamento consanguineo ci sono cugini di secondo grado.
L’inbreeding viene preso in considerazione con l’aiuto del fattore di inbreeding.
Il fattore di inbreeding è la probabilità che due alleli siano identici per origine.
Consideriamo il metodo di calcolo del fattore di inbreeding in un albero genealogico offerto da Wright 1, 2.
Per la ricerca del fattore di inbreeding è necessario:
trovare per i discendenti sposati tutte le vie in un albero genealogico che attraverso l’antenato comune collegano questi discendenti.
contare il numero di passi (alternanze di generazioni) su ogni via.
Allora il fattore di inbreeding è uguale:
 ……(1)
……(1)
dove r è il numero di vie, m1, m2, … mi- numero di passi su ogni via.
Ancora una volta noteremo che il numero di addendi nella somma (1) è uguale al numero di vie che attraverso gli antenati comuni si collegano sposandosi.
Consideriamo casi concreti di alberi genealogici, figura 1. In questa figura il quadrato significa un individuo maschile, il cerchio – individuo femminile. Le linee tratteggiate e le cifre identiche specificano i modi possibili in un albero genealogico che attraverso l’antenato comune (l’uomo o la donna) collegano dei discendenti consanguinei che si sposano. Su alcuni siti di modi, Figura 1с, ci sono due cifre 1 e 2. Si specifica che tali siti sono il comune per i vari modi.
Il matrimonio un padre – figlia è incesto, Figura 1а. Il discendente (donna) è collegato con l’antenato (uomo) in 1 modo con un passo, cioè m = 1. Quindi, c’è fattore di inbreeding.
Ft = 1/2.2-1 = 1/4
C’è il matrimonio fratello – sorella (sibs), Figura 1b. Le cifre specificano il numero della via. Il numero di cifre identiche sulla strada dall’uomo che si sposa alla donna è uguale al numero di passi.
Lasciamo che ogni discendente che si è sposato si colleghi con il partner in due modi con due passi su ogni strada, cioè m = 2. Quindi, c’è il fattore inbreeding.
Ft = 1/2.(2-2 + 2-2) = 1/4
Il matrimonio tra cugini è mostrato nella figura 1с.
Figura 1. Alcuni tipi di inbreeding in un albero genealogico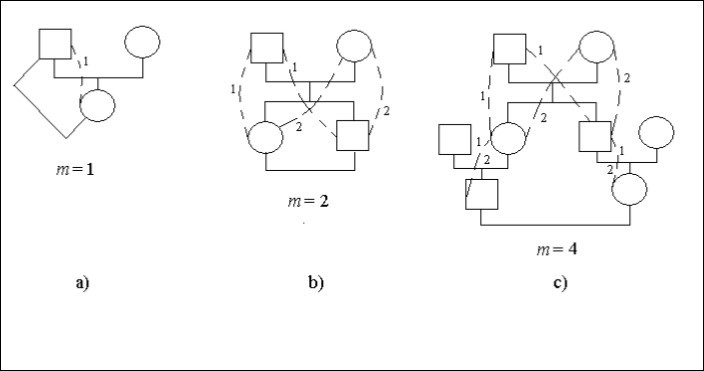
Ogni discendente che si è sposato collega con il partner i 2 modi con 4 passi su ogni modo, cioè m = 4. Quindi, c’è il fattore inbreeding.
Ft = 1/2.(2-4 + 2-4) = 1/16
La formula (1) è facile da capire dalla logica seguente.
Ovviamente ci 1/2 geni del bambino è il comune con ogni genitore, 1/4 – con il nonno e la nonna, 1/8 – con il bisnonno e la bisnonna, ecc. Se dalla donna a qualsiasi antenato conduce la strada con η passi la quota dei geni comuni con questo antenato è uguale 2-η. Se dall’uomo a un qualsiasi antenato si fa strada con μ passi, la quota di geni comuni è uguale a 2-μ. Al matrimonio dell’uomo e della donna con l’antenato comune la quota dei geni comuni con questo antenato sarà 2-η. 2-μ = 2-m dove m = η + μ è il numero totale di passi attraverso l’antenato comune dalla donna fino al matrimonio dell’uomo. La dimensione 1/2 2-m mostra la probabilità che il gene scelto casualmente alla donna sia identico per origine al gene scelto casualmente all’uomo. La stessa dimensione dà il contributo al fattore di inbreeding Ft a senso unico attraverso l’antenato comune dalla donna fino all’uomo che si sposa.
Per esempio, se l’antenato comune sarà lontano dal matrimonio su η = μ = 5 generazioni la probabilità che abbiano il gene comune è uguale. 1/2 2-(5+5) = 1/2048 Questa grandezza all’analisi dell’accoppiamento può essere trascurata. (Tabella 1)
Tabella 1.fattori di consanguineità per alcuni matrimoni consanguinei sono mostrati in aggiunta.
| Il tipo di matrimonio consanguineo matrimonio | Fattore di consanguineità Ft |
| Cugini di secondo grado | 1/32 |
| Zio cugino – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: l’origine degli alleli identici negli autosomi omologhi è non consanguinea (la probabilità di questa ipotesi è P(H1) = 1- Ft )e nasce anche omozigoteаа (la probabilità condizionata di questo evento è P(aa/H1) = q2) o l’origine degli alleli identici è consanguinea (la probabilità di questa ipotesi è P(H2) = Ft ) e nasce omozigoteа (la probabilità condizionata di questo evento è P(aa/H2) = q). La probabilità q dell’occorrenza dell’omozigote aa in quest’ultimo caso è determinata dal fatto che se l’allele a è in un autosoma allora all’origine consanguinea dell’omozigote lo stesso allele deve necessariamente essere e nell’autosoma omologo.
Quindi, la probabilità totale dell’occorrenza dell’omozigote recessivo è uguale:
 ……….(3)
……….(3)
dove si tiene conto p = 1 – q c’è la frequenza dell’allele a dominante.
Similmente si trova la probabilità totale dell’occorrenza dell’omozigote dominante AA in un accoppiamento casuale:
 ……….. (4)
……….. (4)
Quindi, secondo (3) e (4) la frequenza totale degli omozigoti (dominanti e recessivi) nell’albero genealogico inbred aumenta su 2Ftpq. Quindi, la frequenza degli eterozigoti diminuisce a parità di dimensioni e diventa uguale a 2pq – 2pqFt = 2pq(1-Ft) poiché la somma delle frequenze di tutti gli zigoti è uguale a 1.
In considerazione del fattore di consanguineità e anche (3) e (4) la legge di Hardy – Weinberg nella generazione successiva di albero genealogico consanguineo per un genoma autosomico deve essere scritto le distribuzioni dei genotipi degli zigoti come 4:
 …………(5)
…………(5)
dove pn è la frequenza degli alleli A dominanti nella generazione n, qn – la frequenza degli alleli a recessivi, quindi pn + qn = 1.
Il rapporto (5) si riferisce anche al rapporto 5 di Wright. Il rapporto di Wright mostra che in un albero genealogico inbred dopo l’accoppiamento consanguineo degli individui si osservano i seguenti effetti: c’è un aumento della frazione autosomica omozigote in un albero genealogico su Ft pnqne una riduzione della frazione autosomica eterozigote in (1-F1) quelli in confronto con una popolazione panmica.
Ma già attraverso una generazione viene ripristinato l’equilibrio Hardy – Weinberg che specifica la piccola importanza dell’accoppiamento consanguineo separato per un albero genealogico:
 ………(6)
………(6)
Ovviamente, per una popolazione nel suo insieme l’atto separato dell’accoppiamento consanguineo avrà ancora minore importanza che per un albero genealogico.
Lo stesso effetto di variazione della frequenza dei genotipi degli zigoti si osserva anche per i geni legati al sesso.
La distribuzione dei genotipi legati al cromosoma Х nell’albero genealogico panmico è descritta dalla legge di Hardy – Weinberg come 1:
 ………..(7)
………..(7)
La frequenza di un allele dominante A sarà indicata agli uomini pm e alle donne pf. Per gli alleli recessivi A è di conseguenza qm e qf.
Al momento dell’accoppiamento c’è un rapporto di genotipi nelle donne secondo il prodotto (pf + qf) (pm +qm).
Troviamo la probabilità totale dell’occorrenza dell’omozigote recessivo aa all’accoppiamento casuale per i geni della figlia legati al cromosoma X sotto la formula (2). La logica degli eventi è simile al caso degli autosomi, tranne che la probabilità condizionata di un genotipoаа che si verifica dagli alleli non consanguinei secondo la (7) è uguale a P(aa/H1) = qmnqfn. Per gli alleli consanguinei la probabilità condizionale di un genotipoаа è uguale a P(aa/H2) = qf(n+1). Nelle figlie, cioè nella generazione n+1, la probabilità che si verifichi un omozigote aa è determinata dal fatto che se l’allele a si trova in un cromosoma Х, allora all’origine consanguinea dell’omozigote lo stesso allele deve necessariamente trovarsi nel cromosoma Х omologo.
Quindi, la probabilità totale dell’occorrenza dell’omozigote recessivo è uguale:
 ……(8)
……(8)
dove pmn è la frequenza degli alleli dominanti A nella generazione n negli uomini e pfn – nelle donne. Per gli alleli recessivi a di conseguenza qmn e qfn . Inoltre si usa qmn =1 – qmn e pfn = 1 – qfn.
Similmente trovare la probabilità totale dell’occorrenza dell’omozigote dominante con l’uso:
 ,
,
 ……….(9)
……….(9)
e un eterozigote P(Aa) = 1- P(aa) – P(AA) troveremo la distribuzione dei genotipi nei cromosomi Х dell’albero genealogico inbred all’accoppiamento:
 ……..(10)
……..(10)
Si dimostra contemporaneamente che, come negli autosomi, gli additivi inbred nelle frequenze di omozigoti dominanti e recessivi nei cromosomi legati al sesso sono identici.
Un altro modo di trovare il rapporto (10) consisterà nel seguente.
Per prima cosa troviamo la probabilità totale che si verifichi un eterozigote Aa, cioè P(Aa) in occasione dell’accoppiamento consanguineo casuale. Questa probabilità deriva dalla seguente logica di accoppiamento: l’origine degli alleli è non consanguinea (la probabilità di questa ipotesi è P(H1) = 1 – Ft ) sorge anche l’eterozigote Aа (la probabilità condizionata di questo evento è P(Aa/H1) = pmnqfn + pfnqmn, vedi la formula (7)) o l’origine degli alleli è consanguinea (la probabilità di questa ipotesi è P(H2) = Ft) e nasce l’eterozigote Aа (la probabilità condizionata di questo evento è uguale a zero P(Aa/H2) = 0). L’ultima affermazione è definita dal fatto che all’origine consanguinea gli alleli simili nei cromosomi Х omologhi non possono far nascere l’eterozigote Aа costituito da alleli diversi.
Quindi, usando la formula della probabilità totale troviamo la probabilità totale del verificarsi dell’eterozigote Aa:
 ……..(11)
……..(11)
La riduzione della frequenza di un eterozigote Aa avviene come è stato dimostrato in precedenza a causa dell’identico aumento della frequenza degli omozigoti dominanti AA e recessivi aa. Per esempio, l’aumento della frequenza degli omozigoti aa recessivi è uguale:
 ……..(12)
……..(12)
dove la riduzione della frequenza degli eterozigoti Aa relativa all’albero genealogico panmico secondo (7) e (11) è uguale. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) Usando (11) e (12) per aggiornare la (7) per i casi di inbreeding troviamo la distribuzione dei genotipi (10) nei cromosomi Х nell’albero genealogico delle figlie inbred.
Nella generazione seguente la frequenza degli alleli recessivi a alle donne è uguale:
 ……..(13)
……..(13)
Che è pienamente conforme alla stessa frequenza in assenza di inbreeding, cioè c’è il ripristino dell’equilibrio Hardy – Weinberg o è più esatto approccio all’equilibrio.
Il rapporto (7) e (13) mostrano nel complesso che le frequenze alleliche in un albero genealogico per il conto dell’inbreeding non variano. C’è solo una ridistribuzione degli alleli. Una parte degli alleli lascia gli eterozigoti e passa agli omozigoti.