Alcuni esempi delle complesse simmetrie usate nella decorazione dei templi islamici
L’impero islamico stabilitosi in Persia, Medio Oriente, Asia centrale, Nord Africa, Iberia e parte dell’India a partire dall’VIII secolo ha dato significativi contributi alla matematica. Furono in grado di attingere e fondere insieme gli sviluppi matematici sia della Grecia che dell’India.
Una conseguenza della proibizione islamica di raffigurare la forma umana fu l’ampio uso di complessi modelli geometrici per decorare i loro edifici, elevando la matematica alla forma di un’arte. Infatti, col tempo, gli artisti musulmani scoprirono tutte le diverse forme di simmetria che possono essere rappresentate su una superficie bidimensionale.
Il Corano stesso incoraggiò l’accumulo di conoscenza, e un’età dell’oro della scienza e della matematica islamica fiorì durante il periodo medievale dal IX al XV secolo. La Casa della Saggezza fu istituita a Baghdad intorno all’810, e il lavoro iniziò quasi immediatamente a tradurre le principali opere matematiche e astronomiche greche e indiane in arabo.
L’eccezionale matematico persiano Muhammad Al-Khwarizmi fu uno dei primi direttori della Casa della Saggezza nel IX secolo, e uno dei più grandi matematici musulmani. Forse il più importante contributo di Al-Khwarizmi alla matematica fu la sua forte difesa del sistema numerico indù (1 – 9 e 0), che egli riconobbe avere la potenza e l’efficienza necessarie per rivoluzionare la matematica islamica (e, più tardi, occidentale), e che fu presto adottato da tutto il mondo islamico, e più tardi anche dall’Europa.
Al-Khwarizmi diede un altro importante contributo all’algebra, introducendo i fondamentali metodi algebrici della “riduzione” e del “bilanciamento” e fornendo un resoconto esaustivo della risoluzione di equazioni polinomiali fino al secondo grado. In questo modo, contribuì a creare il potente linguaggio matematico astratto usato ancora oggi in tutto il mondo, e permise un modo molto più generale di analizzare problemi diversi da quelli specifici precedentemente considerati da indiani e cinesi.
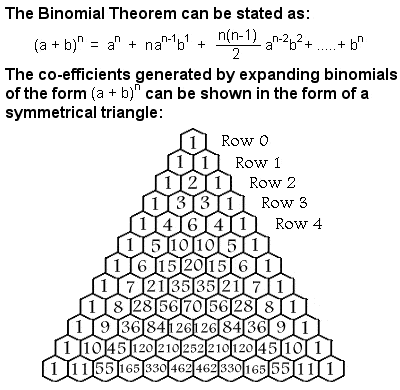
Teorema binomiale
Il matematico persiano del X secolo Muhammad Al-Karaji lavorò per estendere ulteriormente l’algebra, liberandola dalla sua eredità geometrica, e introdusse la teoria del calcolo algebrico. Al-Karaji fu il primo ad usare il metodo della prova per induzione matematica per dimostrare i suoi risultati, provando che la prima affermazione in una sequenza infinita di affermazioni è vera, e poi dimostrando che, se una qualsiasi affermazione della sequenza è vera, allora lo è anche la successiva.
Teorema binomiale
Tra le altre cose, Al-Karaji usò l’induzione matematica per dimostrare il teorema binomiale. Un binomio è un tipo semplice di espressione algebrica che ha solo due termini che sono operati solo da addizione, sottrazione, moltiplicazione ed esponenti di numeri interi positivi, come (x + y)2. I co-efficienti necessari quando un binomio viene espanso formano un triangolo simmetrico, solitamente chiamato Triangolo di Pascal dal nome del matematico francese del XVII secolo Blaise Pascal, anche se molti altri matematici lo avevano studiato secoli prima di lui in India, Persia, Cina e Italia, incluso Al-Karaji.
Qualche centinaio di anni dopo Al-Karaji, Omar Khayyam (forse più noto come poeta e scrittore del “Rubaiyat”, ma importante matematico e astronomo a pieno titolo) generalizzò i metodi indiani per estrarre le radici quadrate e cubiche per includere le radici quarte, quinte e superiori all’inizio del XII secolo. Fece un’analisi sistematica dei problemi cubici, rivelando che in realtà esistevano diversi tipi di equazioni cubiche. Anche se in effetti riuscì a risolvere le equazioni cubiche, e anche se di solito gli si attribuisce il merito di aver individuato le basi della geometria algebrica, fu trattenuto da ulteriori progressi dalla sua incapacità di separare l’algebra dalla geometria, e un metodo puramente algebrico per la soluzione delle equazioni cubiche dovette aspettare altri 500 anni e i matematici italiani del Ferro e Tartaglia.
Trigonometria sferica
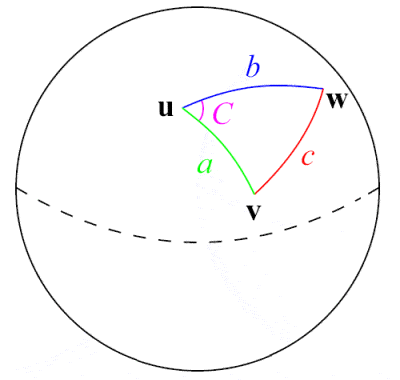
Al-Tusi fu un pioniere nel campo della trigonometria sferica
L’astronomo, scienziato e matematico persiano del XIII secolo Nasir Al-Din Al-Tusi fu forse il primo a trattare la trigonometria come una disciplina matematica separata dall’astronomia. Basandosi sul lavoro precedente di matematici greci come Menelao di Alessandria e sul lavoro indiano sulla funzione seno, diede la prima esposizione estesa della trigonometria sferica, elencando anche i sei casi distinti di un triangolo rettangolo nella trigonometria sferica. Uno dei suoi maggiori contributi matematici fu la formulazione della famosa legge del seno per i triangoli piani, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), sebbene la legge del seno per i triangoli sferici fosse stata scoperta prima dai persiani del X secolo Abul Wafa Buzjani e Abu Nasr Mansur.
Altri matematici musulmani medievali degni di nota sono:
- l’arabo del IX secolo Thabit ibn Qurra, che sviluppò una formula generale con cui si potevano derivare i numeri amicabili, riscoperti molto più tardi sia da Fermat che da Cartesio (i numeri amicabili sono coppie di numeri per cui la somma dei divisori di un numero è uguale all’altro numero, ad es.I divisori propri di 220 sono 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, la cui somma è 284; e i divisori propri di 284 sono 1, 2, 4, 71 e 142, la cui somma è 220).g. 7.375 invece di 73⁄8);
- il geometra arabo del X secolo Ibrahim ibn Sinan, che continuò le ricerche di Archimede sulle aree e sui volumi, e sulle tangenti di un cerchio;
- il persiano dell’XI secolo Ibn al-Haytham (noto anche come Alhazen), che, oltre al suo lavoro rivoluzionario sull’ottica e la fisica, stabilì gli inizi del collegamento tra algebra e geometria, e ideò quello che è ora noto come “il problema di Alhazen” (fu il primo matematico a ricavare la formula per la somma delle quarte potenze, utilizzando un metodo che è facilmente generalizzabile); e
- il persiano del 13° secolo Kamal al-Din al-Farisi, che applicò la teoria delle sezioni coniche per risolvere problemi di ottica, oltre a proseguire il lavoro nella teoria dei numeri come sui numeri amabili, la fattorizzazione e i metodi combinatori;
- il marocchino del 13° secolo Ibn al-Banna al-Marrakushi, i cui lavori includevano argomenti come il calcolo delle radici quadrate e la teoria delle frazioni continuate, così come la scoperta della prima nuova coppia di numeri amicabili dai tempi antichi (17.296 e 18.416, poi riscoperti da Fermat) e il primo uso della notazione algebrica dai tempi di Brahmagupta.
Con l’influenza soffocante dell’impero turco-ottomano a partire dal XIV o XV secolo, la matematica islamica ristagnò e ulteriori sviluppi si spostarono in Europa.
| <
< Torna a Madhava
|
Avanti a Al-Khwarizmi >> |