Utilizzare le variabili strumentali per stabilire la causalità

Svantaggi dell’uso delle variabili strumentali per dimostrare la causalità

Come esempio, si consideri il problema della stima dell’effetto dell’istruzione sui guadagni. La tecnica di stima più semplice, i minimi quadrati ordinari (OLS), genera stime che indicano che un anno aggiuntivo di istruzione è associato a guadagni superiori del 6-10%. Tuttavia, la relazione positiva può essere guidata dall’autoselezione verso l’istruzione, cioè gli individui che hanno più da guadagnare da una maggiore istruzione hanno maggiori probabilità di rimanere. Questo sarà il caso, per esempio, se gli studenti con maggiori capacità trovano più facile studiare, e probabilmente riceverebbero comunque salari più alti. Come tale, la correlazione positiva osservata tra gli anni di istruzione e i salari rifletterebbe in parte il premio sull’abilità, e non potrebbe essere interpretata come il rendimento di un anno di istruzione supplementare, come previsto. Le stime OLS non sarebbero quindi informative sull’effetto di una politica volta ad aumentare gli anni di istruzione. Questo problema è chiamato “distorsione da variabile omessa”. Si verifica quando una variabile (come l’abilità) che non è osservata dal ricercatore è correlata sia al trattamento (più istruzione) che al risultato (guadagni). La direzione (sovrastima o sottostima) e la dimensione della distorsione nelle stime OLS è una funzione del segno e della forza delle correlazioni.

In questo esempio, uno studio di controllo randomizzato (RCT), che comporterebbe l’assegnazione casuale dell’istruzione agli individui e l’osservazione delle differenze nei loro salari nel corso della loro vita, non è semplicemente fattibile per motivi etici. Tuttavia, alcuni esperimenti naturali o quasi-naturali possono avvicinarsi ad alterare la scelta educativa per alcuni gruppi di individui, e come tali, possono essere utilizzati come strumenti. Uno di questi esperimenti naturali è un cambiamento nell’età minima legale in cui gli studenti possono lasciare la scuola (età di uscita dalla scuola). Questo tipo di cambiamento colpisce tutti gli studenti, indipendentemente dalle loro capacità. Agisce quindi come uno shock esterno che non può essere influenzato dal singolo studente.

Numerosi paesi hanno una legislazione che stabilisce l’età in cui gli studenti possono lasciare il sistema educativo. Per esempio, diciamo che un bambino può lasciare la scuola l’ultimo giorno dell’anno scolastico se ha 14 anni entro la fine di agosto. Supponiamo ora che la legislazione sia modificata, in modo che i bambini debbano avere 15 anni entro la fine di agosto per poter lasciare la scuola. Ai bambini che volevano lasciare la scuola a 14 anni viene impedito di farlo, e devono rimanere per un ulteriore anno di scuola. Sotto l’ipotesi (forte) che i bambini sotto le due legislazioni siano simili e affrontino simili condizioni del mercato del lavoro, il cambiamento della legislazione crea un esperimento quasi naturale: indipendentemente dalla loro abilità, alcuni individui saranno colpiti dal cambiamento dell’età di abbandono scolastico e dovranno rimanere per un anno supplementare di scuola, mentre gli alunni con preferenze simili della coorte precedente non lo faranno. Se i ricercatori sapessero chi vuole lasciare la scuola a 14 anni, potrebbero confrontare i risultati degli individui che hanno lasciato la scuola a 14 anni con i risultati degli individui che sono stati costretti a rimanere fino a 15 anni. Questa semplice differenza sarebbe quindi l’effetto causale del rimanere a scuola tra i 14 e i 15 anni. Sfortunatamente, i dati osservazionali non ci permettono di identificare gli individui la cui scelta educativa è stata influenzata dalla riforma; così, sotto la nuova legislazione, gli individui che volevano lasciare la scuola a 15 anni sono indistinguibili da quelli che volevano lasciarla a 14 anni ma dovevano rimanere per un altro anno. Ciò che la riforma fa, tuttavia, è alterare la probabilità di rimanere a scuola, e può quindi essere utilizzata come strumento in quanto influenza la probabilità di trattamento (un altro anno di scuola) senza influenzare il risultato di interesse (ad esempio i guadagni).

Nel 1947, un cambiamento legislativo nel Regno Unito ha aumentato l’età minima per lasciare la scuola da 14 a 15 anni, colpendo i bambini nati nel 1933 e dopo. Questo cambiamento nella legge fornisce l’opportunità di valutare l’effetto della scolarizzazione (aggiuntiva) sui guadagni. Nella Figura 1, il pannello A mostra che la riforma ha influenzato sia la frazione di bambini che lasciano la scuola alla prima opportunità (grafico di sinistra) sia la quantità totale di istruzione completata (grafico di destra). Le stime indicano che la riforma ha aumentato gli anni medi di scolarizzazione per gli uomini di 0,397 anni. Questa stima dell’effetto della riforma (IV) sul trattamento (istruzione) è nota come “regressione di primo stadio”. Se l’istruzione ha un effetto causale sui guadagni, dovremmo osservare che anche i guadagni medi degli individui colpiti dalla riforma sono più alti. Questo è effettivamente il caso, come mostrato nel pannello B della figura 1, che riporta i guadagni medi log per gli uomini. Questa serie mostra una chiara interruzione nel 1933, la cui ampiezza implica che gli individui colpiti dalla riforma guadagnano, in media, l’1,2% di salario in più. Questa seconda stima dell’effetto della riforma (la IV) sul risultato (i guadagni) è nota come “stima in forma ridotta”. Una semplice strategia IV, in questo caso utilizzando uno strumento binario che assume solo due valori (1 per essere influenzato dalla riforma e 0 per non essere influenzato dalla riforma), è il rapporto tra la stima della forma ridotta e la stima del primo stadio. (In questo caso l’effetto causale dell’istruzione supplementare sui guadagni sarebbe 0,012/0,397 = 0,030 e quindi circa il 3%.

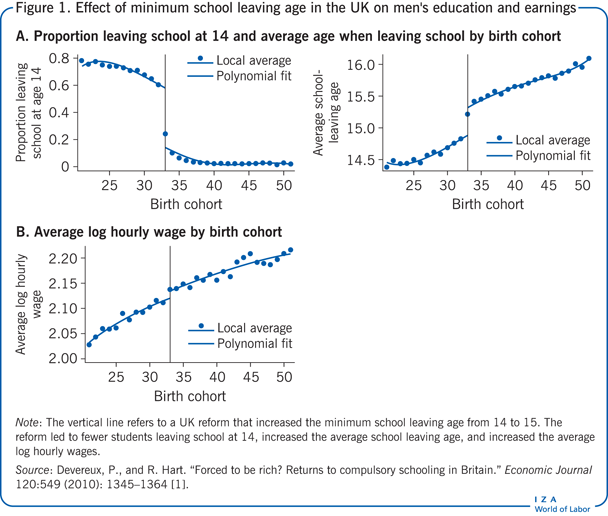
L’intuizione di questo approccio è che l’effetto di un anno in più di istruzione sui salari è fondamentalmente l’effetto della riforma (la IV) sui salari (il risultato) – che è dato nella forma ridotta – scalato dall’effetto che la riforma ha sugli anni di istruzione (il trattamento) – che è ciò che riguarda la stima del primo stadio. Se lo strumento è “rilevante”, cioè ha un effetto sull’istruzione (il trattamento), e se lo strumento influenza i salari “esclusivamente” attraverso il suo effetto sull’istruzione, allora le stime IV possono essere interpretate come l’effetto causale del trattamento sul risultato. Queste due condizioni sono chiamate “rilevanza dello strumento” e “restrizione di esclusione”.

Per riassumere, quando una variabile non osservata come l’abilità correla sia con il trattamento che con il risultato, una stima semplice come OLS sarà distorta a causa dell’autoselezione nel trattamento. Allo stesso modo, se la variabile di trattamento è misurata con errore, la stima OLS sarà distorta verso lo zero. Tuttavia, una stima causale di un trattamento su un risultato può essere recuperata se si trova uno strumento credibile. Uno strumento credibile deve soddisfare due condizioni:

• Rilevanza: lo strumento deve influenzare la probabilità del trattamento. In una regressione del trattamento sullo strumento, nota anche come equazione del primo stadio, il coefficiente sull’IV deve essere sufficientemente forte.

• Restrizione di esclusione: lo strumento influenza il risultato esclusivamente attraverso il suo effetto sul trattamento.

Se tale IV può essere trovato (cioè L’esempio precedente ha presentato la stima di Wald, cioè il rapporto tra le stime di due regressioni: la stima in forma ridotta, proveniente da una regressione dell’esito sullo strumento, e la stima del primo stadio, proveniente da una regressione del trattamento sullo strumento. Questo può essere facilmente calcolato quando lo strumento assume solo due valori. Nel caso più generale, verrà calcolata una cosiddetta stima “two stage least squares” (2SLS), per cui le previsioni del trattamento dall’equazione del primo stadio vengono utilizzate in una regressione del risultato sul trattamento, piuttosto che il vero valore del trattamento. In questo modo, solo la variazione del trattamento proveniente dallo strumento viene utilizzata per spiegare la varianza del risultato. Questo risolve il bias di autoselezione. Nel caso di uno strumento binario (a due valori), le stime Wald e 2SLS saranno identiche (vedi , per esempio). Tuttavia, la difficoltà non sta nell’implementazione di tale stima 2SLS, tutti i pacchetti statistici possono calcolare stime IV, ma nel (a) trovare uno strumento valido e (b) interpretare i risultati. La discussione si concentrerà ora su questi due punti.