レッスンインデックスに戻る|レッスンを順番に行う|印刷用ページ
因数定理
因数定理は剰余定理の結果で、同じ推論に基づいているものである。
余弦定理が指摘するように、多項式 p(x) をその多項式の係数 x – a で割ると、余りは 0 になるのです。 その多項式の分割アルゴリズム式をもう一度見てみましょう。
広告
- (x) = (x – a)q(x) + r(x)
x – a が本当に p(x) の因子であれば、x – a による分割後の余りは 0 になるでしょう。
- (x) = (x – a)q(x)
余弦定理の観点からは、x – a が p(x) の因子である場合、
x = a で合成除算すると余りはゼロになる、ということです。
因子定理のポイントは、余弦定理の逆を行うことです。 多項式を x = a で合成して余りをゼロにすると、x = a は多項式のゼロであるだけでなく (余りの定理による)、x – a も多項式の因子である (因数の定理による)。
余りの定理と同様に、ここでのポイントは、与えられた多項式の与えられた因子による長割を行うことではないのです。 この定理は、あなたがすでに知っていることを繰り返しているのではなく、あなたの人生をよりシンプルにしようとしているのです。 因数定理の演習に直面したとき、あなたは合成除算を適用し、そして余りがゼロであるかどうかをチェックします。
- x – 1 が
f (x) = 2×4 + 3×2 – 5x + 7.
x – 1 が f (x) = 2×4 + 3×2 – 5x + 7 の要因であるために、要因定理は x = 1 が f (x) のゼロでなければならないと述べています。 x – 1 が因数であるかどうかを調べるには、まず x – 1 を 0 に設定して解き、提案された 0 である x = 1 を見つけます。 次に、合成除算を使って、f (x) を x = 1 で割ってみる。 3乗の項がないので、2×4 + 3×2 – 5x + 7のxのべき乗が省略されていることを表すために、合成除算の1行目に「0」を入れることを忘れないように注意します。
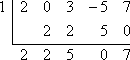
余りはゼロではないので、因子定理は次のように言います:
x – 1 は f (x) の因子ではありません。
- 因数定理を使用して、x + 4 が
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.
x + 4 が因子であれば、(この因数を 0 に設定して解けば)x = -4 は根であることになります。 必要な検証を行うために、x = -4 で f (x) の合成除算を使用すると、余りがゼロになることを確認する必要があります。
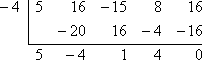
余りはゼロなので、因子定理は、以下のようになります:
x + 4 は 5×4 + 16×3 – 15×2 + 8x + 16 の因子である。
実際には、因数定理は多項式を「完全に」因数分解するときに使用されます。 長割りでいろいろな因数を試すのではなく、合成除算と因数定理を使うことになります。 ある数(多項式の根になりうる数)で割って、合成除算で余りが0になったときは、その数は確かに根であり、したがって「xからその数を引いたもの」が因数であることを意味します。
- -2 と 1/3 が f (x) = 3×4 + 5×3 + x2 + 5x – 2 のゼロであるという事実を使用して、多項式を完全に因数分解します。 Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
もしx = -2が0なら、x + 2 = 0なので、x + 2は因数である。 同様に、x = 1/3が0であれば、x – 1/3=0なので、x – 1/3は因数である。 ゼロを2つ与えることで、因数も2つ与えているのです。 x + 2 と x – 1/3 です。
私は 4 次の多項式から始めたので、これらの与えられた 2 つの因子を分割すると、2 次式が残ります。
因子定理によれば、x + 2 と x – 1/3の既知の因子を使った長い割り算をする必要はないそうです。 その代わりに、関連するゼロ -2 と 1/3 を使った合成除算を使用できます。 以下は、x = -2 で最初の除算を行ったときに得られるものです:
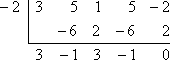
余りはゼロです。これは、-2 が多項式の既知のゼロであると最初に言われたので、予想されたことです。 元の多項式からもう一度やり直すのではなく、今度は残りの多項式の係数 3×3 – x2 + 3x – 1 (合成除算の一番下の行から) に取り組みます。 これをもう 1 つの与えられたゼロである x = 1/3 で割ります。
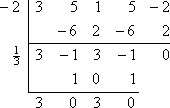
これで、2 次式 3×2 + 3 を解けるようになりました。
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
ゼロが x = -i と x = i なら、要因は x – (-i) と x – (i) 、または x + i と x – i になります。 I need to remember that I divided off a “3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. “The Factor Theorem.” Purplemath. Available from 2016
|