道具変数を使って因果関係を証明する利点
例として、教育が収入に与える影響を推定する問題を考えてみましょう。 最も単純な推定手法である通常の最小二乗法(OLS)では、教育年数が1年増えると、収入が6~10%高くなることを示す推定値が得られます。 しかし、この正の関係は、教育への自己選択によってもたらされている可能性がある。つまり、より多くの教育から最も多くを得ることができる個人は、より多くの教育を受ける可能性が高いのである。 例えば、高い能力を持つ生徒ほど勉強がしやすく、いずれにせよ高い賃金を受け取る可能性がある場合、このようなことが起こる。 したがって、教育年数と賃金の間に見られる正の相関は、部分的に能力プレミアムを反映しており、意図したように教育年数の延長によるリターンとは解釈されない可能性がある。 したがって、OLS推計は、教育年数を増やす政策の効果について情報を提供するものではない。 この問題は、”省略された変数バイアス “と呼ばれる。 これは、研究者が観測していない変数(能力など)が、治療(教育年数の増加)と結果(収入)の両方と相関している場合に発生します。
この例では、個人にランダムに教育を割り当て、生涯の賃金の違いを観察することを伴う無作為化比較試験 (RCT) は、倫理的な理由で実行不可能です。 しかし、自然あるいは準自然的な実験の中には、ある集団の教育選択を変えるに近いものがあり、そのようなものは道具として使うことができる。 そのような自然実験のひとつが、生徒が学校を去ることができる法的な最低年齢(就学年齢)の変更である。 この種の変化は、生徒の能力に関係なく、すべての生徒に影響する。
多くの国が、生徒が教育制度から離れることができる年齢を規定する法律を持っています。 たとえば、8月末までに14歳になれば、その年の最終日に学校を辞めることができるとします。 今、法律が改正され、8月末までに15歳にならないと退学できないようになったとしよう。 14歳で学校を辞めたかった子どもたちは、そうすることができず、さらに1年間学校に残らなければならない。 この2つの法律が適用される子どもは同じようなもので、同じような労働市場の状況に直面するという(強い)仮定の下で、この法改正は準自然実験を引き起こす。つまり、能力に関係なく、ある個人は就学年齢の変更の影響を受け、さらに1年間学校に残る必要があるが、以前のコホートと同じ選好を持っている子どもたちはそうならない。 もし研究者が14歳で学校を辞めたい人を知っていれば、14歳で学校を辞めた人の結果と15歳まで学校に残ることを余儀なくされた人の結果を比較することができるはずである。 この単純な差が、14歳から15歳の間に学校に残ったことの因果的な効果になる。 残念ながら、観測データからは、教育上の選択が改革の影響を受けた個人を特定することはできない。したがって、新しい法律の下では、15歳で学校を辞めたかった個人は、14歳で学校を辞めたかったがもう1年留まらなければならなかった個人と区別がつかないのである。
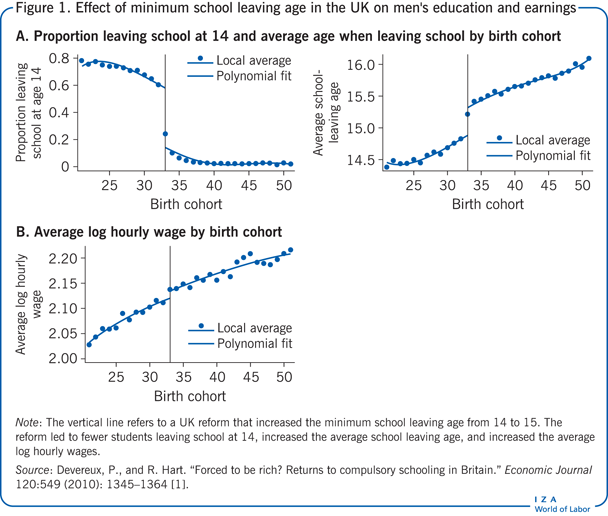
1947年、イギリスでは最低就学年齢が14歳から15歳に引き上げられ、1933年以降に生まれた子供たちが影響を受けました。 この法改正は、(追加の)学校教育が収入に与える影響を評価する機会を提供するものである。 図1のパネルAでは、この改革が、最も早い時期に学校を去る子どもの割合(左側のグラフ)と、修了した学校教育の総量(右側のグラフ)の両方に影響を与えたことが示されている。 推計によると、改革によって男性の平均就学年数が0.397年増加した。 このように、改革(IV)が治療(教育)に及ぼす効果を推定することを、”第一段階回帰 “という。 もし教育が所得に何らかの因果関係を持つとすれば、改革の影響を受けた個人の平均所得も高くなることが観察されるはずである。 図1のパネルB(男性の平均対数所得)に示されるように、これは実際に起こっていることである。 この系列は1933年に明確にブレークしており、その大きさは、改革の影響を受けた人の賃金が平均で1.2%高いことを意味する。 このように、改革(IV)が結果(所得)に与える効果を推定する第二の推定値は、「縮小形式推定値」と呼ばれる。 単純なIV戦略、この場合は2つの値(改革の影響を受けた場合は1、受けていない場合は0)しかとらない2値計器を使って、第1段階推定値に対する縮小形式推定値の比率を求める。 (この場合、追加教育の収益に対する因果効果は0.012/0.397=0.030となり、約3%であることがわかる。
このアプローチの直感は、賃金に対する1年以上の教育の効果は、基本的に改革 (IV) が賃金(結果)に対する効果-これは縮小形式で与えられるのですが、教育(処理)年に対する改革の効果-これは第1段階の推定で行うのですが、それによって倍増する、ということです。 道具が “relevant “であれば、つまり教育(治療)に効果があり、道具が教育への効果を通して賃金に “exclusively “に影響するなら、IV推定値は治療による結果への因果効果と解釈することができる。
まとめると、能力のような観測できない変数が、治療と結果の両方に相関する場合、OLSのような単純な推定では、治療への自己選択によりバイアスがかかってしまうということです。 同様に、治療変数が誤差を持って測定される場合、OLSの推定値はゼロに偏るでしょう。 しかし,信頼できる道具が見つかれば,結果に対する治療の因果推定値を回復することができる. 信頼できる道具は、次の2つの条件を満たさなければならない:
-
妥当性:道具は治療の確率に影響を与えなければならない。
-
第一段階方程式として知られる、道具に対する治療の回帰において、IVの係数は十分に強くなければならない。
除外制限:道具は治療に対するその効果によってのみ結果に影響を与える。
前の例では、Wald推定値、すなわち、2つの回帰からの推定値の比率を示しました:道具に対する結果の回帰から得られる縮小形式の推定値、および道具に対する治療の回帰から得られる第1段階の推定値です。 これは,道具が2つの値しかとらないときに簡単に計算できる. より一般的なケースでは,いわゆる「2段階最小2乗」(2SLS)推定値が計算され,それによって,治療の真値ではなく,第1段階の方程式からの治療の予測値が,治療上の結果の回帰で使用されることになる. このように,機器から来る処置の変動のみが,結果の変動を説明するために使用される. これは,自己選択バイアスを解決する. バイナリ(2値)尺度の場合,Wald と 2SLS 推計は同じになる(たとえば, , を参照). しかし,困難なのは,そのような2SLS推定値の実装ではなく,すべての統計パッケージがIV推定値を計算できることであり,(a) 有効な道具を見つけることと(b) その結果を解釈することである. 以下、この2点に焦点をあてて議論します。