A Beginner’s Guide to Multilayer Perceptrons (MLP)

Contents

• A Brief History of Perceptrons
• Multilayer Perceptrons
• Just Show Me the Code
• FootNotes
• Further Reading

A Brief History of Perceptrons

The perceptron, that neural network whose name evokes how the future looked from the perspective of the 1950s, is a simple algorithm intended to perform binary classification; i.e. it predicts whether input belongs to a certain category of interest or not: fraud or not_fraudcat or not_cat.

パーセプトロンはニューラルネットワークと人工知能の歴史において特別な位置を占めています。なぜなら、その性能に関する最初の誇大広告はミンスキーとパパートによる反論を招き、さらに広範な反発によって数十年にわたってニューラルネットワークの研究に暗雲を投げかけ、2000年代のジェフ・ヒントンの研究によって初めて完全に解けたニューラルネットの冬は、その結果、機械学習コミュニティを席巻することになりました。

パーセプトロンの名付け親であるフランク・ローゼンブラットは、アルゴリズムというよりもデバイスとしてパーセプトロンを普及させました。 コーネル大学で学び、後に講師を務めた心理学者であるローゼンブラットは、米国海軍研究所の資金援助を受け、学習する機械を作ったのである。

パーセプトロンは線形分類器、つまり、2つのカテゴリを直線で区切って入力を分類するアルゴリズムである。 入力は通常、特徴ベクトルxwby = w * x + b.

パーセプトロンは、入力重みを使って線形結合を形成し（時には非線形活性化関数に出力を通し）、複数の実数値入力に基づいて一つの出力を生成します。

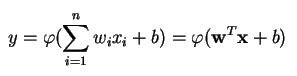
ここで、w は重みのベクトル、x は入力ベクトル、b はバイアス、phi は非線形活性化関数です。

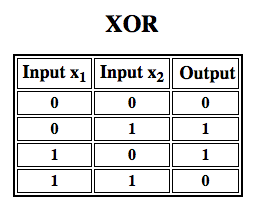
ローゼンブラットは単層パーセプトロンを構築しました。 つまり、彼のハードウェアアルゴリズムは、ニューラルネットワークが特徴階層をモデル化することを可能にする多層を含んでいなかったのである。 そのため、浅いニューラルネットワークであり、ミンスキーとパパートがその著書で示したような、XOR関数（入力が1つの特性か別の特性のどちらかを示し、両方は示さない場合に発動するXOR演算子、「exclusive OR」の略）などの非線形分類を行うことができなかった。

強化学習をシミュレーションに適用する」

Multilayer Perceptrons (MLP)

多層パーセプトロンに関するその後の研究で、他の多くの非線形関数と同様に XOR 演算子を近似できることが示されました。

ローゼンブラットが1943年に考案されたマッカロク・ピッツ・ニューロンをベースにパーセプトロンを作ったように、パーセプトロン自体も、多層パーセプトロンのような大きな機能においてのみ有用であることがわかる構成要素となっています2。

多層パーセプトロンは、ディープラーニングのハローワールドであり、ディープラーニングについて学ぶときに始めるのに適した場所です。 複数のパーセプトロンで構成されています。 信号を受け取る入力層、入力に関する判断や予測を行う出力層、そしてその間にある、MLPの真の計算エンジンである任意の数の隠れ層で構成されています。

多層パーセプトロンは，教師あり学習問題によく応用されます3。つまり，入力と出力のペアのセットで学習し，それらの入力と出力の間の相関（または依存関係）をモデル化することを学びます。 学習では、誤差を最小にするためにモデルのパラメータ、すなわち重みとバイアスを調整する。 バックプロパゲーションは、誤差に対して重みとバイアスの調整を行うために使用され、誤差自体は平均二乗誤差（RMSE）など、さまざまな方法で測定することができます。

MLPなどのフィードフォワードネットワークは、テニスやピンポンのようなものです。 それらは主に2つの運動、つまり一定の往復運動に関わっています。 推測と回答のピンポンは，一種の加速度科学と考えることができます。なぜなら，それぞれの推測は，私たちが知っていると思っていることのテストであり，それぞれの回答は私たちがどれほど間違っているかを知らせるフィードバックだからです。

前方通過では、信号の流れは入力層から隠れ層を通って出力層に移動し、出力層の決定は基底真実ラベルに対して測定されます。

後方通過では、逆伝播と微積分の鎖法則を用いて、MLPを通してさまざまな重みとバイアスに関する誤差関数の偏微分が逆伝播されます。 この微分法によって，勾配，つまり誤差の風景が得られ，それに沿って，MLPを誤差の最小値に一段階近づけるようにパラメータが調整されます． これは，確率的勾配降下法などの勾配に基づく最適化アルゴリズムで行うことができます． ネットワークは，誤差がこれ以上小さくならないようになるまで，そのテニスゲームを続けます．

脚注

ここで指摘すべき興味深い点は、ソフトウェアとハードウェアはフローチャート上に存在するということです。 FPGA のようなチップがプログラムされ、または ASIC が構築されて、あるアルゴリズムがシリコンに焼き付けられるとき、私たちはそれをより速く動作させるために 1 レベル下のソフトウェアを実装しているに過ぎないのです。 同様に、シリコンに焼き付けられたもの、あるいはローゼンブラットのマークIのようにライトやポテンショメーターで配線されたものも、コードで記号的に表現することができるのです。 アラン・ケイが “本当に真剣にソフトウェアを考えている人は、自分でハードウェアを作るべきだ “と言ったのは、このためだ。 しかし、タダ飯はない。つまり、アルゴリズムをシリコンに焼き付けることで得られるスピードは、柔軟性を失うし、その逆もまた然りである。 機械学習では、アルゴリズムがデータに触れることで変化していくので、これは本当に問題なのです。 たとえば、現在 GPU によって最も速く処理されている線形代数演算などです。

2）あなたの考えは、より複雑でより有用なアルゴリズムの次のステップに傾くかもしれません。 私たちは、1 つのニューロンから層と呼ばれる複数のニューロンへと移動し、多層パーセプトロンと呼ばれる 1 つの層から複数の層へと移動します。 マイクロソフトがImageNetの優勝者であるResNetで行ったように、150以上の層を持つMLPを1層から数層にすることはできるのでしょうか。 あるいは，MLPの正しい組み合わせは，多くのアルゴリズムのアンサンブルで，一種の計算民主主義で最良の予測に投票することなのでしょうか？ それとも、グラフ畳み込みネットワークで行っているように、あるアルゴリズムを別のアルゴリズムに埋め込んでいるのでしょうか?

3）より複雑で最先端の方法が存在するにもかかわらず、おそらく世界で最も洗練された AI 企業である Google で、さまざまなタスクに広く使用されています。 A Probabilistic Model for Information Storage and Organization in the Brain, Cornell Aeronautical Laboratory, Psychological Review, by Frank Rosenblatt, 1958 (PDF)