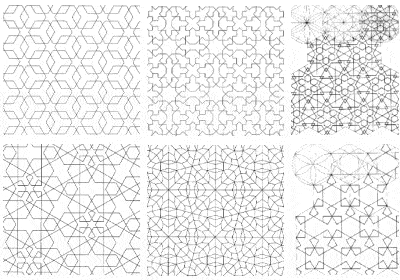
イスラム寺院装飾に用いられる複雑な対称性の例
8世紀以降ペルシア、中東、中央アジア、北アフリカ、イベリア、インドの一部にわたって成立したイスラム帝国は数学に対して大きな貢献を行っています。
また、「人体表現」を禁止した結果、複雑な幾何学模様が多用され、数学は芸術の域に達しています。
『クーラン』は知識の蓄積を奨励し、9世紀から15世紀にかけて中世の科学と数学の黄金期を築いたのです。
ペルシャの優れた数学者であるムハンマド・アル・クワリズミーは、9世紀に知恵の家の初期のディレクターを務め、初期のイスラム数学者の中で最も偉大な人物の一人であった。 アル・クワリズミーは、ヒンズー教の数詞体系(1-9と0)を強く支持し、それがイスラム(後に西洋)の数学に革命を起こすのに必要な力と効率を持っていると認識し、すぐにイスラム世界全体、そして後にヨーロッパにも取り入れられた。
アル・クワリズミのもう一つの重要な貢献は代数学で、彼は「還元」と「平衡」という基本的な代数的方法を導入し、2次までの多項式方程式の解法について網羅的に説明したのである。 このように、彼は現在も世界中で使われている強力な抽象的数学言語の創造に貢献し、それまでインド人や中国人が考えていたような特定の問題だけでなく、より一般的な問題の分析方法を可能にしたのである。
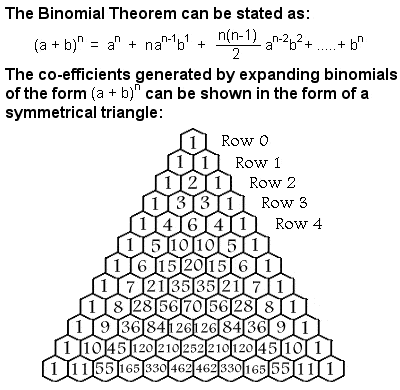
二項定理
10世紀のペルシャの数学者ムハンマド・アル・カラジは、幾何学的遺産から解放し、さらに代数学を拡張しようと取り組み、代数計算の理論を紹介しました。 アル・カラジは、数学的帰納法による証明という方法を初めて使いました。無限に続く文の最初の文が真であることを証明し、次に、その文のどれかが真であれば、次の文もそうであることを証明しました。
二項定理
とりわけ、アル・カラジは二項定理を証明するのに、数学的帰納法を使いました。 二項式とは、加算、減算、乗算、および (x + y)2 のような正の整数指数によってのみ操作される、たった 2 つの項を持つ単純なタイプの代数式である。 二項式を展開したときに必要となる係数は対称な三角形を形成し、17世紀のフランスの数学者ブレーズ・パスカルにちなんで通常パスカルの三角形と呼ばれるが、パスカルより何世紀も前にインド、ペルシャ、中国、イタリアでアル・カラジなど多くの数学者がこの研究をおこなっていた。
アル・カラジから数百年後、オマル・ハイヤーム (おそらく詩人および「ルバイヤート」の作者としてよく知られていますが、彼自身は重要な数学者および天文学者でした) が、12世紀初頭にインドの平方根および立方根抽出方法を一般化して、4、5、およびそれ以上の根を含むようになりました。 彼は3次方程式の問題を体系的に分析し、実際にはいくつかの異なる種類の3次方程式が存在することを明らかにした。 しかし、代数学と幾何学を分離することができず、純粋に代数学的な3次方程式の解法は、さらに500年後、イタリアの数学者デルフェロとタルターリャが開発するのを待つしかなかったのである。
球面三角法
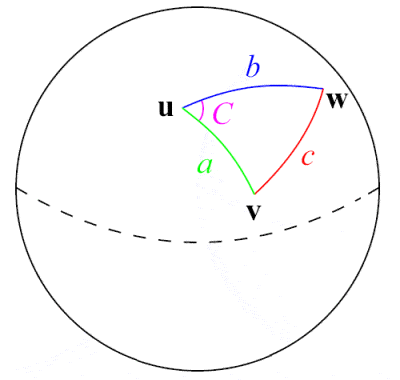
アル=トゥシは球面三角法の分野のパイオニアです
13世紀のペルシャの天文学者で科学者で数学者のナシール・アル=ディン・トゥシはおそらく天文学とは別の数学分野としての三角法を扱った最初の人でしょう。 アレクサンドリアのメネラウスなどギリシャの数学者やインドの正弦関数に関する研究を基に、球面三角法における直角三角形の6つの異なるケースをリストアップするなど、球面三角法について初めて広範囲な解説を行いました。 彼の数学的貢献の1つは、平面三角形に対する有名な正弦の法則、a/(sin A) = b⁄(sin B) = c⁄(sin C)を定式化したことだが、10世紀のペルシャ人アブル・ワファ・ブジャニとアブ・ナスル・マンスールによって球面三角形の正弦法則はそれ以前に発見されていた。
特筆すべき他の中世のイスラム数学者は次のとおりです。
- 9 世紀のアラブ人 Thabit ibn Qurra は、可能数を導き出す一般式を開発し、後に Fermat とデカルトによって再発見されました (可能数とは、一方の数の除数の和が他方の数に等しい数の組を指します。
- 10世紀のアラブの数学者 Abul Hasan al-Uqlidisi は、アラビア数字の位置の使用、特に分数の代わりに小数を使用することを示す現存する最古のテキストを書きました (例.g. 7.375 insead of 73⁄8)
- 10世紀のアラブの幾何学者Ibrahim ibn Sinanは、面積や体積、円の接線に関するアルキメデスの研究を続けました。11 世紀のペルシャ人 Ibn al-Haytham (別名 Alhazen) は、光学と物理に関する画期的な仕事に加え、代数と幾何学の間のリンクの始まりを確立し、現在「Alhazen の問題」として知られているものを考案しました (彼は、容易に一般化できる方法を使用して 4 乗の和の公式を導き出した最初の数学者でした)。 13世紀のペルシャ人カマル・アルディン・アルファリシは、光学問題の解決に円錐断面の理論を応用し、また円満数、因数分解、組合せ法などの数論的な研究を進めた。
- 13世紀のモロッコ人イブン・アルバンナ・アル・マラクーシは、平方根の計算や継続分数の理論などを研究し、古代以来初めての新しい組の有効数(17,296 と 18,416 、後にフェルマーによって再発見)を発見、ブラフマグプタ以来初めての代数表記法を使用した。
14~15世紀以降、トルコ・オスマン帝国の息苦しさから、イスラムの数学は停滞し、さらなる発展はヨーロッパに移った。
| << マダヴァに戻る | アル-に進む。Khwarizmi >> |