MATEMATICĂ ISLAMICĂ

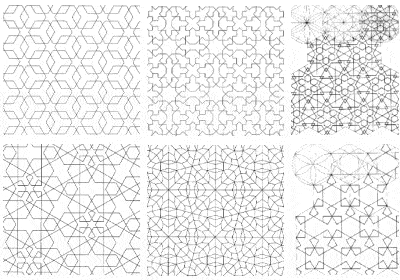
Câteva exemple de simetrii complexe folosite în decorarea templelor islamice

Imperiul islamic stabilit în Persia, Orientul Mijlociu, Asia Centrală, Africa de Nord, Iberia și în unele părți ale Indiei începând cu secolul al VIII-lea a adus contribuții semnificative în domeniul matematicii. Aceștia au fost capabili să se bazeze pe dezvoltările matematice atât din Grecia, cât și din India și să le îmbine între ele.

O consecință a interdicției islamice de a reprezenta forma umană a fost utilizarea pe scară largă a modelelor geometrice complexe pentru decorarea clădirilor lor, ridicând matematica la forma unei arte. De fapt, în timp, artiștii musulmani au descoperit toate formele diferite de simetrie care pot fi reprezentate pe o suprafață bidimensională.

Coranul însuși a încurajat acumularea de cunoștințe, iar o epocă de aur a științei și matematicii islamice a înflorit de-a lungul perioadei medievale, între secolele al IX-lea și al XV-lea. Casa Înțelepciunii a fost înființată la Bagdad în jurul anului 810, iar lucrările de traducere în arabă a principalelor lucrări de matematică și astronomie grecești și indiene au început aproape imediat.

Excelentul matematician persan Muhammad Al-Khwarizmi a fost unul dintre primii directori ai Casei Înțelepciunii în secolul al IX-lea și unul dintre cei mai mari matematicieni musulmani timpurii. Poate că cea mai importantă contribuție a lui Al-Khwarizmi la matematică a fost susținerea fermă a sistemului numeric hindus (1 – 9 și 0), căruia i-a recunoscut puterea și eficiența necesare pentru a revoluționa matematica islamică (și, mai târziu, cea occidentală) și care a fost în curând adoptat de întreaga lume islamică, iar mai târziu și de Europa.

O altă contribuție importantă a lui Al-Khwarizmi a fost algebra, iar el a introdus metodele algebrice fundamentale de „reducere” și „echilibrare” și a oferit o prezentare exhaustivă a rezolvării ecuațiilor polinomiale până la gradul al doilea. În acest fel, el a contribuit la crearea puternicului limbaj matematic abstract utilizat și astăzi în întreaga lume și a permis o modalitate mult mai generală de analiză a problemelor, altele decât cele specifice luate în considerare anterior de indieni și chinezi.

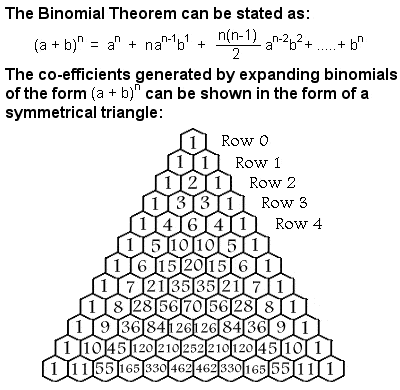
Teorema binomială

Matematicianul persan din secolul al X-lea Muhammad Al-Karaji a lucrat pentru a extinde și mai mult algebra, eliberând-o de moștenirea sa geometrică, și a introdus teoria calculului algebric. Al-Karaji a fost primul care a folosit metoda demonstrației prin inducție matematică pentru a-și dovedi rezultatele, demonstrând că primul enunț dintr-o secvență infinită de enunțuri este adevărat, iar apoi demonstrând că, dacă oricare dintre enunțurile din secvență este adevărat, atunci și următorul este adevărat.

Teorema binomială

Printre altele, Al-Karaji a folosit inducția matematică pentru a demonstra teorema binomială. Un binom este un tip simplu de expresie algebrică care are doar doi termeni asupra cărora se operează doar prin adunare, scădere, înmulțire și exponenți cu numere întregi pozitive, cum ar fi (x + y)2. Coeficienții necesari la expandarea unui binom formează un triunghi simetric, denumit de obicei Triunghiul lui Pascal, după numele matematicianului francez din secolul al XVII-lea Blaise Pascal, deși mulți alți matematicieni îl studiaseră cu secole înaintea sa în India, Persia, China și Italia, inclusiv Al-Karaji.

La câteva sute de ani după Al-Karaji, Omar Khayyam (poate mai bine cunoscut ca poet și scriitor al „Rubaiyat”, dar un important matematician și astronom de sine stătător) a generalizat metodele indiene de extragere a rădăcinilor pătrate și cubice pentru a include rădăcinile a patra, a cincea și superioare la începutul secolului al XII-lea. El a efectuat o analiză sistematică a problemelor cubice, dezvăluind că existau de fapt mai multe tipuri diferite de ecuații cubice. Deși a reușit, de fapt, să rezolve ecuații cubice și deși i se atribuie de obicei meritul de a fi identificat bazele geometriei algebrice, a fost împiedicat să facă progrese suplimentare din cauza incapacității sale de a separa algebra de geometrie, iar o metodă pur algebrică pentru rezolvarea ecuațiilor cubice a trebuit să aștepte încă 500 de ani și pe matematicienii italieni del Ferro și Tartaglia.

Trigonometria sferică

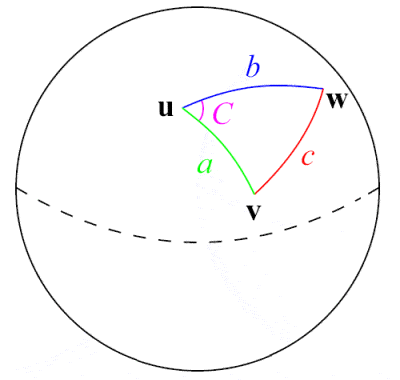
Al-Tusi a fost un pionier în domeniul trigonometriei sferice

Astronomul, omul de știință și matematicianul persan din secolul al XIII-lea Nasir Al-Din Al-Tusi a fost probabil primul care a tratat trigonometria ca pe o disciplină matematică separată, distinctă de astronomie. Bazându-se pe lucrările anterioare ale matematicienilor greci, cum ar fi Menelaus din Alexandria, și pe lucrările indiene privind funcția sinus, el a făcut prima expunere amplă a trigonometriei sferice, enumerând inclusiv cele șase cazuri distincte de triunghi dreptunghic în trigonometria sferică. Una dintre contribuțiile sale matematice majore a fost formularea faimoasei legi a sinusurilor pentru triunghiurile plane, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), deși legea sinusurilor pentru triunghiurile sferice fusese descoperită anterior de către perșii Abul Wafa Buzjani și Abu Nasr Mansur din secolul al X-lea.

Alți matematicieni musulmani medievali demni de luat în seamă includ:

• arabeanul din secolul al IX-lea Thabit ibn Qurra, care a dezvoltat o formulă generală prin care puteau fi derivate numerele amiabile, redescoperite mult mai târziu atât de Fermat, cât și de Descartes (numerele amiabile sunt perechi de numere pentru care suma divizorilor unui număr este egală cu celălalt număr, de ex.ex. divizorii proprii ai lui 220 sunt 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 și 110, din care suma este 284; iar divizorii proprii ai lui 284 sunt 1, 2, 4, 71 și 142, din care suma este 220);
• matematicianul arab din secolul al X-lea Abul Hasan al-Uqlidisi, care a scris cel mai vechi text care a supraviețuit și care arată utilizarea pozițională a cifrelor arabe și, în special, utilizarea zecimalelor în locul fracțiilor (de ex.g. 7.375 în loc de 73⁄8);
• geometrul arab din secolul al X-lea Ibrahim ibn Sinan, care a continuat cercetările lui Arhimede asupra ariilor și volumelor, precum și asupra tangentelor unui cerc;
• persianul din secolul al XI-lea Ibn al-Haytham (cunoscut și sub numele de Alhazen), care, pe lângă lucrările sale revoluționare în domeniul opticii și al fizicii, a stabilit începuturile legăturii dintre algebră și geometrie și a conceput ceea ce astăzi este cunoscut sub numele de „problema lui Alhazen” (a fost primul matematician care a derivat formula pentru suma puterilor a patra, folosind o metodă ușor generalizabilă); și
• persanul din secolul al XIII-lea Kamal al-Din al-Farisi, care a aplicat teoria secțiunilor conice pentru a rezolva probleme de optică, precum și a continuat lucrările în teoria numerelor, cum ar fi cele privind numerele amiabile, factorizarea și metodele combinatorii;
• marocanul din secolul al XIII-lea Ibn al-Banna al-Marrakushi, ale cărui lucrări au inclus subiecte precum calculul rădăcinilor pătrate și teoria fracțiilor continue, precum și descoperirea primei perechi noi de numere amiabile din cele mai vechi timpuri (17.296 și 18.416, redescoperite ulterior de Fermat) și prima utilizare a notației algebrice de la Brahmagupta încoace.

Cu influența sufocantă a Imperiului otoman turc începând cu secolul al XIV-lea sau al XV-lea, matematica islamică a stagnat, iar dezvoltările ulterioare s-au mutat în Europa.

< Înapoi la Madhava

Întoarceți la Al…Khwarizmi >>