Întoarceți-vă la Indexul lecțiilor | Parcurgeți lecțiile în ordine | Print-friendly page
Teorema factorilor
Teorema factorilor este un rezultat al Teoremei restului și se bazează pe același raționament. Dacă nu ați citit lecția despre Teorema restului, revedeți mai întâi acel subiect și apoi reveniți aici.
Așa cum subliniază Teorema restului, dacă împărțiți un polinom p(x) cu un factor x – a al acelui polinom, atunci veți obține un rest zero. Să ne uităm din nou la acea expresie a algoritmului de diviziune a polinomului:
Advertisment
- Utilizați Teorema Factorilor pentru a determina dacă x – 1 este un factor al lui
f (x) = 2×4 + 3×2 – 5x + 7. - Utilizând Teorema Factorilor, verificați că x + 4 este un factor al lui
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16. - Folosind faptul că -2 și 1/3 sunt zerouri ale lui f (x) = 3×4 + 5×3 + x2 + 5x – 2, factorizați complet polinomul. Copyright © Elizabeth Stapel 2002-2011 Toate drepturile rezervate
p(x) = (x – a)q(x) + r(x)
Dacă x – a este într-adevăr un factor al lui p(x), atunci restul după împărțirea cu x – a va fi zero. Adică:
p(x) = (x – a)q(x)
În termenii Teoremei restului, aceasta înseamnă că, dacă x – a este un factor al lui p(x), atunci restul, atunci când facem împărțirea sintetică cu
x = a, va fi zero.
Punctul Teoremei factorului este invers față de Teorema restului: Dacă împărțiți sintetic un polinom cu x = a și obțineți un rest zero, atunci, nu numai că x = a este un zero al polinomului (prin amabilitatea Teoremei restului), dar x – a este, de asemenea, un factor al polinomului (prin amabilitatea Teoremei factorului).
La fel ca și în cazul Teoremei restului, scopul aici nu este de a face împărțirea lungă a unui polinom dat cu un factor dat. Această Teoremă nu repetă ceea ce știți deja, ci încearcă în schimb să vă facă viața mai simplă. Atunci când vă confruntați cu un exercițiu de Teoremă a factorilor, veți aplica împărțirea sintetică și apoi veți verifica dacă restul este zero.
Pentru ca x – 1 să fie un factor al lui f (x) = 2×4 + 3×2 – 5x + 7, Teorema Factorilor spune că x = 1 trebuie să fie un zero al lui f (x). Pentru a testa dacă x – 1 este un factor, voi seta mai întâi x – 1 egal cu zero și voi rezolva pentru a găsi zero-ul propus, x = 1. Apoi voi folosi împărțirea sintetică pentru a împărți f (x) la x = 1. Deoarece nu există niciun termen cubic, voi avea grijă să nu uit să introduc un „0” pe prima linie a împărțirii sintetice pentru a reprezenta puterea omisă a lui x în 2×4 + 3×2 – 5x + 7:
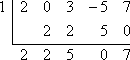
Din moment ce restul nu este zero, atunci teorema factorului spune că:
x – 1 nu este un factor al lui f (x).
Dacă x + 4 este un factor, atunci (stabilind acest factor egal cu zero și rezolvând) x = -4 este o rădăcină. Pentru a face verificarea necesară, trebuie să verific că, atunci când folosesc împărțirea sintetică pe f (x), cu x = -4, obțin un rest egal cu zero:
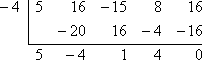
Rămășița este zero, deci Teorema Factorilor spune că:
x + 4 este un factor al lui 5×4 + 16×3 – 15×2 + 8x + 16.
În practică, teorema factorului este utilizată atunci când se factorulizează polinoame „complet”. În loc să încercați diverși factori folosind diviziunea lungă, veți folosi diviziunea sintetică și Teorema factorilor. Ori de câte ori împărțiți la un număr (fiind o potențială rădăcină a polinomului) și obțineți un rest zero la împărțirea sintetică, aceasta înseamnă că numărul este într-adevăr o rădăcină și, prin urmare, „x minus numărul” este un factor. Apoi veți continua împărțirea cu polinomul mai mic rezultat, continuând până când veți ajunge la un factor liniar (deci ați găsit toți factorii) sau pătratic (căruia îi puteți aplica formula pătratică).
Dacă x = -2 este un zero, atunci x + 2 = 0, deci x + 2 este un factor. În mod similar, dacă x = 1/3 este un zero, atunci x – 1/3 = 0, deci x – 1/3 este un factor. Dându-mi două dintre zerouri, mi-au dat, de asemenea, doi factori: x + 2 și x – 1/3.
Din moment ce am început cu un polinom de gradul patru, atunci voi rămâne cu o cuadratură după ce voi împărți acești doi factori dați. Pot să rezolv acea pătratică folosind formula pătratică sau o altă metodă.
Teorema factorilor spune că nu trebuie să fac împărțirea lungă cu factorii cunoscuți x + 2 și x – 1/3. În schimb, pot folosi împărțirea sintetică cu zerourile asociate -2 și 1/3. Iată ce obțin atunci când fac prima împărțire cu x = -2:
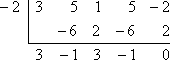
Rămășița este zero, ceea ce este de așteptat pentru că mi-au spus la început că -2 este un zero cunoscut al polinomului. În loc să o iau de la capăt cu polinomul inițial, voi lucra acum la factorul polinomial rămas din polinomul 3×3 – x2 + 3x – 1 (de pe rândul de jos al împărțirii sintetice). Îl voi împărți cu celălalt zero dat, x = 1/3:
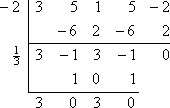
Aceasta îmi lasă cuadratara 3×2 + 3, pe care o pot rezolva:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Dacă zerourile sunt x = -i și x = i, atunci factorii sunt x – (-i) și x – (i), sau x + i și x – i. I need to remember that I divided off a „3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. „The Factor Theorem.” Purplemath. Available from 2016
|