Zpět na rejstřík lekcí | Udělat lekce v pořadí | Stránka vhodná pro tisk
Faktorová věta
Faktorová věta je výsledkem Věty o zbytku a je založena na stejné úvaze. Pokud jste nečetli lekci o Faktorové větě, projděte si nejprve toto téma a pak se sem vraťte.
Jak upozorňuje Faktorová věta, dělíte-li polynom p(x) činitelem x – a tohoto polynomu, pak dostanete nulový zbytek. Podívejme se znovu na ono vyjádření polynomu pomocí Algoritmu dělení:
Reklama
p(x) = (x – a)q(x) + r(x)
Je-li x – a skutečně činitelem p(x), pak zbytek po dělení x – a bude nulový. To znamená:
p(x) = (x – a)q(x)
Z hlediska Věty o zbytku to znamená, že pokud je x – a činitelem p(x), pak zbytek, když provedeme syntetické dělení
x = a, bude nulový.
Smysl Věty o faktoru je opačný než u Věty o zbytku:
Jestliže synteticky dělíme polynom x = a a dostaneme nulový zbytek, pak nejenže x = a je nulou polynomu (díky Remainderově větě), ale x – a je také faktorem polynomu (díky Faktorové větě).
Stejně jako v případě Remainderovy věty, ani zde nejde o to provést dlouhé dělení daného polynomu daným faktorem. Tato věta neopakuje to, co již znáte, ale naopak se vám snaží zjednodušit život. Když se setkáte s cvičením na Faktorovou větu, použijete syntetické dělení a pak zkontrolujete, zda je zbytek nulový.
- Pomocí Faktorové věty určete, zda x – 1 je činitelem
f (x) = 2×4 + 3×2 – 5x + 7.
Aby x – 1 bylo činitelem f (x) = 2×4 + 3×2 – 5x + 7, Faktorová věta říká, že x = 1 musí být nulou f (x). Abych otestoval, zda je x – 1 činitelem, nastavím nejprve x – 1 na nulu a vyřeším, abych našel navrženou nulu, x = 1. Poté použiji syntetické dělení a vydělím f (x) číslem x = 1. Protože neexistuje kubický člen, budu dávat pozor, abych nezapomněl do prvního řádku syntetického dělení vložit „0“, která bude představovat vynechanou mocninu x ve tvaru 2×4 + 3×2 – 5x + 7. Budu se snažit o to, aby se v prvním řádku syntetického dělení objevila „0“:
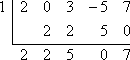
Jelikož zbytek není nulový, pak Faktorová věta říká, že:
x – 1 není činitel f (x).
- Pomocí Faktorové věty ověřte, že x + 4 je činitelem
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.
Je-li x + 4 činitelem, pak (stanovením tohoto činitele na nulu a řešením) x = -4 je kořen. K požadovanému ověření potřebuji ověřit, že když použiji syntetické dělení na f (x), přičemž x = -4, dostanu nulový zbytek:
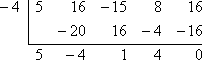
Zbytek je nulový, takže Faktorová věta říká, že:
x + 4 je činitel 5×4 + 16×3 – 15×2 + 8x + 16.
V praxi se Faktorová věta používá při „úplném“ dělení mnohočlenů. Místo zkoušení různých činitelů pomocí dlouhého dělení se použije syntetické dělení a Faktorová věta. Kdykoli budete dělit číslem (které je potenciálním kořenem mnohočlenu) a při syntetickém dělení dostanete nulový zbytek, znamená to, že číslo je skutečně kořenem, a tedy „x minus číslo“ je faktorem. Pak budete pokračovat v dělení s výsledným menším polynomem a pokračovat tak dlouho, dokud nedojdete k lineárnímu činiteli (takže jste našli všechny činitele) nebo ke kvadratickému (na který můžete použít kvadratický vzorec).
- S využitím faktu, že -2 a 1/3 jsou nuly f (x) = 3×4 + 5×3 + x2 + 5x – 2, vynásobte polynom úplně. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
Jestliže x = -2 je nula, pak x + 2 = 0, takže x + 2 je činitel. Podobně je-li x = 1/3 nula, pak x – 1/3 = 0, takže x – 1/3 je činitel. Tím, že mi dali dvě z nul, mi dali také dva činitele:
Jelikož jsem začal s mnohočlenem čtvrtého stupně, pak mi po vydělení těchto dvou daných činitelů zůstane čtyřčlen. Tento čtyřčlen mohu vyřešit pomocí kvadratického vzorce nebo nějakou jinou metodou.
Faktorová věta říká, že nemusím provádět dlouhé dělení se známými činiteli x + 2 a x – 1/3.
Věta o faktorech říká, že se známými činiteli x + 2 a x – 1/3 nemusím provádět dlouhé dělení. Místo toho mohu použít syntetické dělení s přidruženými nulami -2 a 1/3. Tady je to, co dostanu, když provedu první dělení s x = -2:
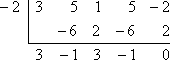Zbytek je nula, což se dalo očekávat, protože mi na začátku řekli, že -2 je známá nula polynomu. Než abych začínal znovu s původním polynomem, budu nyní pracovat se zbývajícím činitelem polynomu 3×3 – x2 + 3x – 1 (ze spodního řádku syntetického dělení). Ten vydělím druhou danou nulou, x = 1/3:
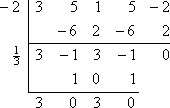
Tímto mi zůstává čtverec 3×2 + 3, který mohu vyřešit:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Jsou-li nuly x = -i a x = i, pak činitelé jsou x – (-i) a x – (i), nebo x + i a x – i.
Pokud jsou nuly x = -i a x = i, pak činitelé jsou x – (-i) a x – (i). I need to remember that I divided off a „3“ when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. „The Factor Theorem.“ Purplemath. Available from 2016
|