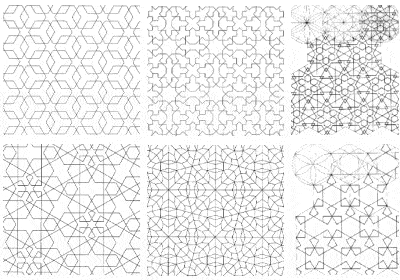
Několik příkladů složitých symetrií používaných v islámské chrámové výzdobě
Islámská říše vzniklá v Persii, na Blízkém východě, ve střední Asii, severní Africe, na Pyrenejském poloostrově a v některých částech Indie od 8. století významně přispěla k rozvoji matematiky. Dokázala čerpat a spojit dohromady matematický vývoj Řecka i Indie.
Jedním z důsledků islámského zákazu zobrazování lidské podoby bylo rozsáhlé používání složitých geometrických vzorů k výzdobě svých staveb, čímž povýšila matematiku do podoby umění. Muslimští umělci totiž postupem času objevili všechny různé formy symetrie, které lze zobrazit na dvourozměrném povrchu.
Sám Korán podporoval hromadění vědomostí a po celé období středověku od 9. do 15. století vzkvétal zlatý věk islámské vědy a matematiky. Kolem roku 810 byl v Bagdádu založen Dům moudrosti a téměř okamžitě se začalo pracovat na překladu hlavních řeckých a indických matematických a astronomických děl do arabštiny.
Významný perský matematik Muhammad al-Chwarizmi byl v 9. století prvním ředitelem Domu moudrosti a jedním z největších raných muslimských matematiků. Al-Chwarizmího pravděpodobně nejvýznamnějším přínosem pro matematiku byla jeho důrazná obhajoba hinduistické číselné soustavy (1 – 9 a 0), o níž si uvědomoval, že má sílu a účinnost potřebnou k revoluci v islámské (a později i západní) matematice, a kterou brzy přijal celý islámský svět a později i Evropa.
Al-Chwarizmiho dalším významným přínosem byla algebra, zavedl základní algebraické metody „redukce“ a „vyvažování“ a podal vyčerpávající popis řešení polynomiálních rovnic až do druhého stupně. Tímto způsobem pomohl vytvořit mocný abstraktní matematický jazyk, který se dodnes používá po celém světě, a umožnil mnohem obecnější způsob analýzy jiných problémů než jen specifických problémů, o nichž dříve uvažovali Indové a Číňané.
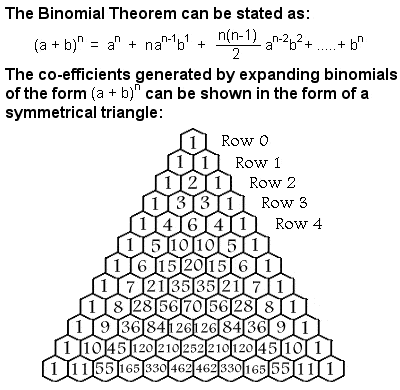
Binomická věta
Perský matematik z 10. století Muhammad Al-Karadží pracoval na dalším rozšíření algebry, osvobodil ji od jejího geometrického dědictví a zavedl teorii algebraického kalkulu. Al-Karadží jako první použil k důkazu svých výsledků metodu důkazu matematickou indukcí, kdy dokázal, že první výrok v nekonečné posloupnosti výroků je pravdivý, a poté dokázal, že pokud je pravdivý kterýkoli výrok v posloupnosti, pak je pravdivý i další.
Binomická věta
Matematickou indukci použil Al-Karadží mimo jiné k důkazu binomické věty. Binomický výraz je jednoduchý typ algebraického výrazu, který má právě dva členy, s nimiž se operuje pouze pomocí sčítání, odčítání, násobení a kladných celočíselných exponentů, například (x + y)2 . Koeficienty potřebné při rozkladu binomu tvoří symetrický trojúhelník, který se obvykle označuje jako Pascalův trojúhelník podle francouzského matematika Blaise Pascala ze 17. století, ačkoli se jím zabývala řada dalších matematiků již několik století před ním v Indii, Persii, Číně a Itálii, včetně Al-Karadžiho.
Několik set let po Al-Karadžim Omar Chajjám (možná známější jako básník a autor „Rubajátu“, ale sám významný matematik a astronom) na počátku 12. století zobecnil indické metody získávání odmocnin a krychlových kořenů tak, aby zahrnovaly i čtvrté, páté a vyšší kořeny. Provedl systematickou analýzu kubických úloh a odhalil, že ve skutečnosti existuje několik různých druhů kubických rovnic. Ačkoli se mu řešení kubických rovnic skutečně podařilo a ačkoli se mu obvykle připisují základy algebraické geometrie, v dalším pokroku mu bránila neschopnost oddělit algebru od geometrie a na čistě algebraickou metodu řešení kubických rovnic si museli počkat dalších 500 let a italští matematici del Ferro a Tartaglia.
Sférická trigonometrie
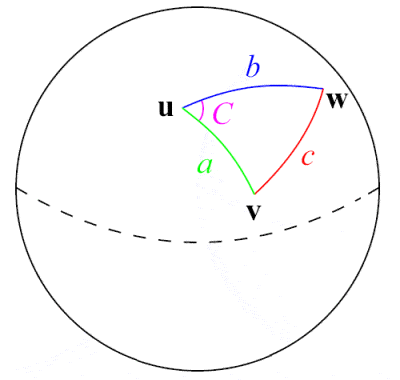
Al-Tusi byl průkopníkem v oblasti sférické trigonometrie
Perský astronom, vědec a matematik 13. století Nasir Al-Din Al-Tusi byl pravděpodobně prvním, kdo se trigonometrií zabýval jako samostatnou matematickou disciplínou, odlišnou od astronomie. Na základě dřívějších prací řeckých matematiků, jako byl Meneláos Alexandrijský, a indických prací o funkci sinus, podal první rozsáhlý výklad sférické trigonometrie, včetně výčtu šesti různých případů pravoúhlého trojúhelníku ve sférické trigonometrii. Jedním z jeho hlavních matematických přínosů byla formulace slavného sinusového zákona pro rovinné trojúhelníky: a⁄(sin A) = b⁄(sin B) = c⁄(sin C), ačkoli sinusový zákon pro sférické trojúhelníky objevili již dříve Peršané Abul Wafa Buzjani a Abu Nasr Mansur v 10. století.
Mezi další středověké muslimské matematiky, kteří stojí za zmínku, patří:
- Arab Thabit ibn Qurra z 9. století, který vypracoval obecný vzorec, podle něhož lze odvodit smíšená čísla, znovuobjevená mnohem později Fermatem i Descartem(smíšená čísla jsou dvojice čísel, u nichž se součet dělitelů jednoho čísla rovná druhému číslu, např.např. vlastní dělitelé čísla 220 jsou 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 a 110, jejichž součet je 284; a vlastní dělitelé čísla 284 jsou 1, 2, 4, 71 a 142, jejichž součet je 220);
- arabský matematik z 10. století Abul Hasan al-Uqlidisi, který napsal nejstarší dochovaný text ukazující poziční používání arabských číslic a zejména používání desetinných čísel místo zlomků (např.g. 7.375 místo 73⁄8);
- arabský geometr 10. století Ibrahim ibn Sinan, který pokračoval v Archimédově zkoumání ploch a objemů a také tečen kruhu;
- peršan Ibn al-Hajtham (známý také jako Alhazen) z 11. století, který kromě průkopnických prací v oblasti optiky a fyziky vytvořil počátky spojení mezi algebrou a geometrií a vymyslel to, co je dnes známo jako „Alhazenův problém“ (jako první matematik odvodil vzorec pro součet čtvrtých mocnin metodou, která se dá snadno zobecnit); a
- Peršan Kamal al-Din al-Farisi ze 13. století, který použil teorii kuželoseček k řešení optických problémů a pokračoval v práci v teorii čísel, například v teorii smíšených čísel, faktorizaci a kombinatorických metodách;
- marocký Ibn al-Banna al-Marrakushi ze 13. století, jehož práce zahrnovaly témata jako výpočet odmocnin a teorie pokračujících zlomků, jakož i objev první nové dvojice amikable čísel od starověku (17 296 a 18 416, později znovuobjevená Fermatem) a první použití algebraického zápisu od dob Brahmagupty.
S dusivým vlivem turecké Osmanské říše od 14. nebo 15. století islámská matematika stagnovala a další vývoj se přesunul do Evropy.
| << Zpět na Madhava | Předat na Al-Khwarizmi >> |