Použití instrumentálních proměnných k prokázání kauzality

Výhody použití instrumentálních proměnných k prokázání kauzality

Jako příklad uveďme problematiku odhadu vlivu vzdělání na výdělky. Nejjednodušší technika odhadu, obyčejné nejmenší čtverce (OLS), vytváří odhady, které naznačují, že jeden rok vzdělání navíc je spojen s výdělky, které jsou o 6-10 % vyšší . Tento pozitivní vztah však může být způsoben samovýběrem ke vzdělávání, tj. jedinci, kteří mohou z vyššího vzdělání nejvíce získat, pravděpodobněji zůstanou. Tak tomu bude například v případě, že pro žáky s vyššími schopnostmi je studium snazší a pravděpodobně by i tak dostávali vyšší mzdu. Pozorovaná pozitivní korelace mezi roky vzdělávání a mzdami by tak částečně odrážela prémii za schopnosti a nemohla by být interpretována jako výnos z dalšího roku vzdělávání, jak bylo zamýšleno. Odhady OLS by tedy neměly vypovídací hodnotu o účinku politiky zaměřené na zvýšení počtu let vzdělávání. Tento problém se nazývá „zkreslení opomenutých proměnných“. Dochází k němu, když proměnná (např. schopnost), kterou výzkumník nepozoruje, koreluje jak s léčbou (vyšší vzdělání), tak s výsledkem (výdělky). Směr (nadhodnocení nebo podhodnocení) a velikost zkreslení v odhadech OLS je funkcí znaménka a síly korelací.

V tomto příkladu není randomizovaná kontrolní studie (RCT), která by znamenala náhodné přidělení vzdělání jednotlivcům a sledování rozdílů v jejich mzdách v průběhu života, z etických důvodů jednoduše proveditelná. Některé přirozené nebo kvazipřirozené experimenty se však mohou blížit změně volby vzdělání u některých skupin jednotlivců a jako takové je lze použít jako nástroje. Jedním z takových přirozených experimentů je změna zákonem stanoveného minimálního věku, ve kterém mohou žáci ukončit školní docházku (věk ukončení školní docházky). Tento typ změny se týká všech žáků nezávisle na jejich schopnostech. Působí tedy jako vnější šok, který jednotlivý žák nemůže ovlivnit.

V řadě zemí je legislativně stanovena věková hranice, ve které mohou žáci opustit vzdělávací systém. Řekněme například, že dítě může opustit školu poslední den školního roku, pokud mu bude do konce srpna 14 let. Předpokládejme nyní, že se legislativa změní tak, že dětem musí být do konce srpna 15 let, aby mohly opustit školu. Dětem, které chtěly opustit školu ve 14 letech, je to znemožněno a musí zůstat na další rok školní docházky. Za (silného) předpokladu, že děti podle obou legislativ jsou si podobné a čelí podobným podmínkám na trhu práce, vytváří změna legislativy kvazi-přirozený experiment: nezávisle na jejich schopnostech budou někteří jedinci ovlivněni změnou věku ukončení školní docházky a budou muset zůstat další rok ve škole, zatímco žáci s podobnými preferencemi z předchozí kohorty nikoli. Pokud by výzkumníci věděli, kdo chce opustit školu ve 14 letech, mohli by porovnat výsledky jedinců, kteří školu opustili ve 14 letech, s výsledky jedinců, kteří byli nuceni zůstat do 15 let. Tento jednoduchý rozdíl by pak představoval kauzální efekt setrvání ve škole mezi 14. a 15. rokem života. Bohužel data z pozorování nám neumožňují identifikovat jednotlivce, jejichž volba vzdělávání byla reformou ovlivněna; takže podle nové legislativy jsou jednotlivci, kteří chtěli opustit školu v 15 letech, nerozlišitelní od těch, kteří chtěli odejít ve 14 letech, ale museli zůstat ještě jeden rok. Reforma nicméně mění pravděpodobnost setrvání ve škole, a proto ji lze použít jako nástroj, protože ovlivňuje pravděpodobnost léčby (další rok školní docházky), aniž by ovlivnila výsledek, který nás zajímá (např. výdělek).

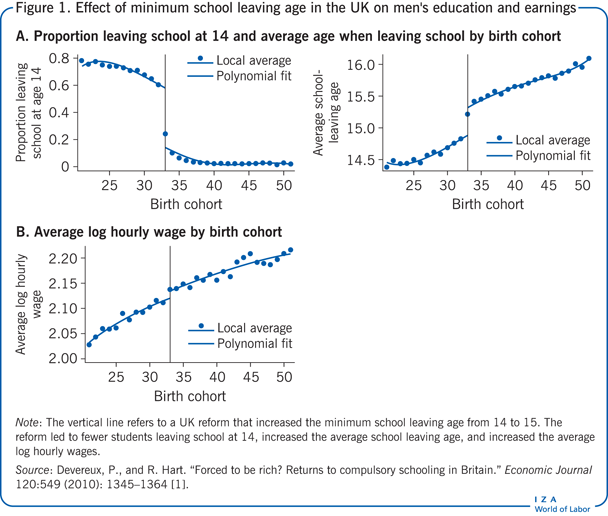
V roce 1947 došlo ve Spojeném království k legislativní změně, která zvýšila minimální věk pro ukončení školní docházky ze 14 na 15 let, což se týkalo dětí narozených v roce 1933 a později. Tato změna zákona poskytuje příležitost vyhodnotit vliv (dodatečné) školní docházky na výdělky . Na obrázku 1 v panelu A je vidět, že reforma ovlivnila jak podíl dětí, které ukončily školní docházku při nejbližší příležitosti (levý graf), tak celkovou délku absolvované školní docházky (pravý graf). Odhady ukazují, že reforma zvýšila průměrný počet let školní docházky u mužů o 0,397 roku. Tento odhad vlivu reformy (IV) na zacházení (vzdělání) je znám jako „regrese prvního stupně“. Pokud má vzdělání nějaký kauzální vliv na výdělky, měli bychom pozorovat, že průměrné výdělky jednotlivců, kterých se reforma dotkla, jsou také vyšší. Tak tomu skutečně je, jak ukazuje panel B grafu 1, který uvádí průměrné logaritmické výdělky mužů. Tato řada vykazuje v roce 1933 jasný zlom, z jehož velikosti vyplývá, že jednotlivci postižení reformou vydělávají v průměru o 1,2 % vyšší mzdy. Tento druhý odhad vlivu reformy (IV) na výsledek (výdělky) je znám jako „odhad v redukované podobě“. Jednoduchá strategie IV, v tomto případě s použitím binárního nástroje, který nabývá pouze dvou hodnot (1 pro ovlivnění reformou a 0 pro neovlivnění reformou), je poměrem redukovaného odhadu k odhadu první fáze. (Tento poměr je také znám jako Waldův odhad.) V tomto případě by byl kauzální účinek dodatečného vzdělání na výdělky 0,012/0,397 = 0,030, tedy přibližně 3 %.

Intuice tohoto přístupu spočívá v tom, že vliv jednoho roku vzdělání navíc na mzdy je v podstatě vliv reformy (IV) na mzdy (výsledek) – který je dán v redukované formě – zvětšený o vliv, který má reforma na roky vzdělání (zacházení) – což je to, o čem je odhad prvního stupně. Pokud je nástroj „relevantní“, tj. má vliv na vzdělání (léčbu), a pokud nástroj ovlivňuje mzdy „výhradně“ prostřednictvím svého vlivu na vzdělání, pak lze odhady IV interpretovat jako kauzální vliv léčby na výsledek. Tyto dvě podmínky se nazývají „relevance nástroje“ a „omezení vyloučení“.

Shrňme, že pokud nepozorovaná proměnná, jako je schopnost, koreluje jak s léčbou, tak s výsledkem, bude jednoduchý odhad, jako je OLS, zkreslený v důsledku samovýběru do léčby. Podobně, pokud je proměnná léčby měřena s chybou, bude odhad OLS zkreslený směrem k nule. Příčinný odhad vlivu léčby na výsledek však lze získat, pokud lze nalézt věrohodný nástroj. Věrohodný nástroj musí splňovat dvě podmínky:

• Relevance: nástroj musí ovlivňovat pravděpodobnost léčby. V regresi léčby na nástroj, známé také jako rovnice prvního stupně, musí být koeficient IV dostatečně silný.

• Omezení vyloučení: nástroj ovlivňuje výsledek výhradně prostřednictvím svého vlivu na léčbu.

Pokud lze takový IV najít (tj. je splněno jak omezení relevance, tak omezení vyloučení), pak lze uplatnit strategii IV k získání kauzálního účinku léčby na výsledek.

Předchozí příklad představil Waldův odhad, tj. poměr odhadů ze dvou regresí: odhadu v redukované podobě, který pochází z regrese výsledku na nástroj, a odhadu prvního stupně, který pochází z regrese léčby na nástroj. To lze snadno vypočítat, pokud nástroj nabývá pouze dvou hodnot. V obecnějším případě se vypočítá takzvaný „dvoustupňový odhad nejmenších čtverců“ (2SLS), kdy se v regresi výsledku na léčbu použijí předpovědi léčby z rovnice prvního stupně, nikoli skutečná hodnota léčby. K vysvětlení rozptylu výsledku se tak použije pouze variance léčby pocházející z nástroje. To pak řeší zkreslení samovýběru. V případě binárního (dvouhodnotového) nástroje budou Waldovy a 2SLS odhady totožné (viz například ,). Potíž však nespočívá v implementaci takového odhadu 2SLS, všechny statistické balíky umí vypočítat odhady IV, ale v a) nalezení platného nástroje a b) interpretaci výsledků. Diskuse se nyní zaměří na tyto dva body.