Wellengeschwindigkeit auf einer gespannten Saite
Um zu sehen, wie die Geschwindigkeit einer Welle auf einer Saite von der Spannung und der linearen Dichte abhängt, betrachten wir einen Impuls, der über eine gespannte Saite gesendet wird (Abbildung \(\PageIndex{1}\)). Wenn die gespannte Saite in der Gleichgewichtslage ruht, ist die Spannung in der Saite \(F_T\) konstant. Betrachten wir ein kleines Element der Saite mit einer Masse gleich \(\Delta m = \mu \Delta x\). Das Massenelement befindet sich in Ruhe und im Gleichgewicht, und die Spannungskraft auf beiden Seiten des Massenelements ist gleich und entgegengesetzt.
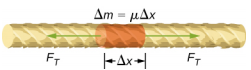
Zieht man an einer unter Spannung stehenden Saite, bewegt sich eine Transversalwelle in positiver x-Richtung, wie in Abbildung \(\PageIndex{2}\) dargestellt. Das Massenelement ist klein, wird aber in der Abbildung vergrößert dargestellt, um es sichtbar zu machen. Das kleine Masseelement schwingt aufgrund der Rückstellkraft der Saite senkrecht zur Wellenbewegung und bewegt sich nicht in x-Richtung. Die Spannung FT in der Saite, die in positiver und negativer x-Richtung wirkt, ist annähernd konstant und unabhängig von Ort und Zeit.
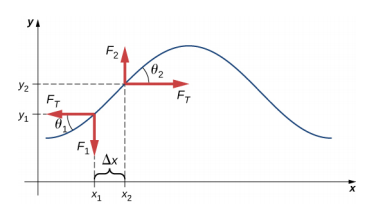
Angenommen, die Neigung der verschobenen Saite gegenüber der horizontalen Achse ist klein. Die Nettokraft auf das Element der Saite, die parallel zur Saite wirkt, ist die Summe aus der Spannung in der Saite und der Rückstellkraft. Die x-Komponenten der Zugkraft heben sich auf, so dass die Nettokraft gleich der Summe der y-Komponenten der Kraft ist. Der Betrag der x-Komponente der Kraft ist gleich der horizontalen Zugkraft der Saite \(F_T\), wie in Abbildung \(\PageIndex{2}\) dargestellt. Um die y-Komponenten der Kraft zu erhalten, ist zu beachten, dass tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}\) und \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}\). \(\tan \theta\) ist gleich der Steigung einer Funktion in einem Punkt, die gleich der partiellen Ableitung von y nach x in diesem Punkt ist. Daher ist \(\frac{F_{1}}{F_{T}}\) gleich der negativen Steigung der Zeichenkette bei x1 und \(\frac{F_{2}}{F_{T}}\) gleich der Steigung der Zeichenkette bei x2:
Die Nettokraft auf das kleine Massenelement kann geschrieben werden als
\ \ldotp\]
Nach dem zweiten Newtonschen Gesetz ist die Nettokraft gleich der Masse mal der Beschleunigung. Die lineare Dichte der Saite µ ist die Masse pro Länge der Saite, und die Masse des Teils der Saite ist \(\mu \Delta\)x,
= \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\right) \ldotp\]
Teilt man durch FT\(\Delta\)x und nimmt den Grenzwert, wenn \(\Delta\)x gegen Null geht,
\}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]
Erinnern Sie sich, dass die lineare Wellengleichung lautet
Daher,
lösen wir für \(v\), sehen wir, dass die Geschwindigkeit der Welle auf einer Saite von der Spannung und der linearen Dichte abhängt
Die Geschwindigkeit einer Welle auf einer Saite unter Spannung
Die Geschwindigkeit eines Impulses oder einer Welle auf einer Saite unter Spannung kann mit der Gleichung
gefunden werden, wobei \(F_T\) die Spannung in der Saite und \(µ\) die Masse pro Länge der Saite ist.
Beispiel 16.5: Die Wellengeschwindigkeit einer Gitarrenfeder
Bei einer sechssaitigen Gitarre hat die hohe E-Saite eine lineare Dichte von \(\mu_{High\; E}\) = 3,09 x 10-4 kg/m und die niedrige E-Saite hat eine lineare Dichte von \(\mu_{Low\; E}\) = 5,78 x 10-3 kg/m. (a) Wenn die Saite mit dem hohen E gezupft wird und dabei eine Welle in der Saite entsteht, wie hoch ist die Geschwindigkeit der Welle, wenn die Spannung der Saite 56,40 N beträgt? (b) Die lineare Dichte der tiefen E-Saite ist etwa 20 Mal größer als die der hohen E-Saite. Müsste die Spannung größer oder kleiner sein als bei der hohen E-Saite, damit sich die Wellen durch die niedrige E-Saite mit der gleichen Geschwindigkeit ausbreiten wie durch die hohe E-Saite? Wie hoch wäre die ungefähre Spannung? (c) Berechnen Sie die Spannung der niedrigen E-Saite, die für die gleiche Wellengeschwindigkeit benötigt wird.
Strategie
- Die Geschwindigkeit der Welle kann aus der linearen Dichte und der Spannung \(v = \sqrt{\frac{F_{T}}{\mu}}\) ermittelt werden.
- Aus der Gleichung v = \(\sqrt{\frac{F_{T}}{\mu}}) ergibt sich, dass bei einer Erhöhung der linearen Dichte um einen Faktor von fast 20 die Spannung um den Faktor 20 erhöht werden müsste.
- Wenn man die Geschwindigkeit und die lineare Dichte kennt, kann die Geschwindigkeitsgleichung für die Spannungskraft FT = \(\mu\)v2 gelöst werden.
Lösung
- Benutzen Sie die Geschwindigkeitsgleichung, um die Geschwindigkeit zu finden: $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\; N}{3.09 \times 10^{-4}\; kg/m}} = 427.23\; m/s \ldotp$$
- Die Spannung müsste um einen Faktor von etwa 20 erhöht werden. Die Spannung wäre etwas geringer als 1128 N.
- Benutzen Sie die Geschwindigkeitsgleichung, um die tatsächliche Spannung zu ermitteln: $$F_{T} = \mu v^{2} = (5,78 \mal 10^{-3}\; kg/m)(427,23\; m/s)^{2} = 1055,00\; N \ldotp$$
- Diese Lösung liegt innerhalb von 7 % der Näherung.
Bedeutung
Die Standardtöne der sechs Saiten (hohes E, B, G, D, A, tiefes E) sind so gestimmt, dass sie beim Zupfen mit den Grundfrequenzen (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz und 82,41 Hz) schwingen. Die Frequenzen hängen von der Geschwindigkeit der Wellen auf der Saite und der Wellenlänge ab. Die sechs Saiten haben unterschiedliche lineare Dichten und werden durch Veränderung der Saitenspannung „gestimmt“. Wir werden in Interferenz von Wellen sehen, dass die Wellenlänge von der Länge der Saiten und den Randbedingungen abhängt. Um andere Töne als die Grundtöne zu spielen, werden die Längen der Saiten durch Drücken auf die Saiten verändert.
Übung 16.5
Die Wellengeschwindigkeit einer Welle auf einer Saite hängt von der Spannung und der linearen Massendichte ab. Was passiert mit der Geschwindigkeit der Wellen auf der Saite, wenn die Spannung verdoppelt wird?