Contents
- A Brief History of Perceptrons
- Multilayer Perceptrons
- Just Show Me the Code
- FootNotes
- Further Reading
A Brief History of Perceptrons
The perceptron, that neural network whose name evokes how the future looked from the perspective of the 1950s, is a simple algorithm intended to perform binary classification; i.e. it predicts whether input belongs to a certain category of interest or not: fraud or not_fraudcat or not_cat.
El perceptrón ocupa un lugar especial en la historia de las redes neuronales y la inteligencia artificial, ya que el bombo inicial sobre su rendimiento condujo a una refutación por parte de Minsky y Papert, y a una reacción más amplia que arrojó una sombra sobre la investigación de redes neuronales durante décadas, un invierno de redes neuronales que se descongeló por completo sólo con la investigación de Geoff Hinton en la década de 2000, cuyos resultados han barrido desde entonces la comunidad de aprendizaje de máquinas.
Frank Rosenblatt, padrino del perceptrón, lo popularizó como un dispositivo más que como un algoritmo. El perceptrón llegó por primera vez al mundo en forma de hardware.1 Rosenblatt, un psicólogo que estudió y posteriormente dio clases en la Universidad de Cornell, recibió financiación de la Oficina de Investigación Naval de Estados Unidos para construir una máquina que pudiera aprender. Su máquina, el perceptrón Mark I, tenía este aspecto.

Un perceptrón es un clasificador lineal; es decir, es un algoritmo que clasifica la entrada separando dos categorías con una línea recta. La entrada es típicamente un vector de características x multiplicado por pesos w y sumado a un sesgo by = w * x + b.
Un perceptrón produce una única salida basada en varias entradas de valor real formando una combinación lineal usando sus pesos de entrada (y a veces pasando la salida a través de una función de activación no lineal). Así es como se puede escribir en matemáticas:
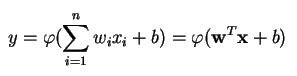
donde w denota el vector de pesos, x es el vector de entradas, b es el sesgo y phi es la función de activación no lineal.
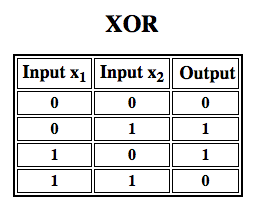
Rosenblatt construyó un perceptrón de una sola capa. Es decir, su hardware-algoritmo no incluía múltiples capas, que permiten a las redes neuronales modelar una jerarquía de características. Se trataba, por tanto, de una red neuronal poco profunda, lo que impedía a su perceptrón realizar una clasificación no lineal, como la función XOR (un operador XOR se dispara cuando la entrada presenta un rasgo u otro, pero no ambos; significa «OR exclusivo»), como Minsky y Papert mostraron en su libro.
Aplicar el aprendizaje por refuerzo a las simulaciones»
Perceptrones multicapa (MLP)
Los trabajos posteriores con perceptrones multicapa han demostrado que son capaces de aproximar un operador XOR así como muchas otras funciones no lineales.
Así como Rosenblatt basó el perceptrón en una neurona McCulloch-Pitts, concebida en 1943, también los propios perceptrones son bloques de construcción que sólo demuestran ser útiles en funciones tan grandes como los perceptrones multicapa.2)
El perceptrón multicapa es el hola mundo del aprendizaje profundo: un buen lugar para empezar cuando se está aprendiendo sobre el aprendizaje profundo.
Un perceptrón multicapa (MLP) es una red neuronal artificial profunda. Está compuesta por más de un perceptrón. Se componen de una capa de entrada para recibir la señal, una capa de salida que toma una decisión o predicción sobre la entrada, y entre esas dos, un número arbitrario de capas ocultas que son el verdadero motor computacional del MLP. Los MLP con una capa oculta son capaces de aproximar cualquier función continua.
Los perceptrones multicapa suelen aplicarse a problemas de aprendizaje supervisado3: se entrenan con un conjunto de pares de entrada-salida y aprenden a modelar la correlación (o las dependencias) entre esas entradas y salidas. El entrenamiento consiste en ajustar los parámetros, o los pesos y sesgos, del modelo para minimizar el error. La retropropagación se utiliza para hacer esos ajustes de pesos y sesgos en relación con el error, y el error en sí mismo puede medirse de varias maneras, incluyendo el error cuadrático medio (RMSE).
Las redes de avance como los MLP son como el tenis, o el ping pong. Participan principalmente en dos movimientos, un ida y vuelta constante. Se puede pensar en este ping pong de conjeturas y respuestas como una especie de ciencia acelerada, ya que cada conjetura es una prueba de lo que creemos saber, y cada respuesta es una retroalimentación que nos hace saber lo equivocados que estamos.
En el paso hacia adelante, el flujo de la señal se mueve desde la capa de entrada a través de las capas ocultas hasta la capa de salida, y la decisión de la capa de salida se mide contra las etiquetas de la verdad básica.
En el paso hacia atrás, utilizando la retropropagación y la regla de la cadena de cálculo, las derivadas parciales de la función de error con respecto a los diversos pesos y sesgos se retropropagan a través del MLP. Este acto de diferenciación nos da un gradiente, o un paisaje de error, a lo largo del cual los parámetros pueden ser ajustados a medida que mueven el MLP un paso más cerca del mínimo de error. Esto puede hacerse con cualquier algoritmo de optimización basado en el gradiente, como el descenso estocástico del gradiente. La red sigue jugando esa partida de tenis hasta que el error no puede bajar más. Este estado se conoce como convergencia.
Notas al pie
1) Lo interesante de señalar aquí es que el software y el hardware existen en un diagrama de flujo: el software puede expresarse como hardware y viceversa. Cuando se programan chips como las FPGAs, o se construyen ASICs para hornear un determinado algoritmo en el silicio, simplemente estamos implementando el software un nivel más abajo para que funcione más rápido. Del mismo modo, lo que se hornea en silicio o se cablea con luces y potenciómetros, como el Mark I de Rosenblatt, también puede expresarse simbólicamente en código. Por eso Alan Kay ha dicho que «la gente que se toma realmente en serio el software debería fabricar su propio hardware». Pero no hay almuerzo gratis; es decir, lo que se gana en velocidad al hornear algoritmos en el silicio, se pierde en flexibilidad, y viceversa. Esto resulta ser un verdadero problema en lo que respecta al aprendizaje automático, ya que los algoritmos se alteran a sí mismos mediante la exposición a los datos. El reto consiste en encontrar aquellas partes del algoritmo que permanezcan estables aunque cambien los parámetros; por ejemplo, las operaciones de álgebra lineal que actualmente son procesadas con mayor rapidez por las GPU.
2) Tus pensamientos pueden inclinarse hacia el siguiente paso en algoritmos cada vez más complejos y también más útiles. Pasamos de una neurona a varias, llamada capa; pasamos de una capa a varias, llamada perceptrón multicapa. ¿Podemos pasar de un MLP a varios, o simplemente seguimos acumulando capas, como hizo Microsoft con su ganador de ImageNet, ResNet, que tenía más de 150 capas? ¿O es la combinación correcta de MLP un conjunto de muchos algoritmos que votan en una especie de democracia computacional sobre la mejor predicción? ¿O se trata de incrustar un algoritmo dentro de otro, como hacemos con las redes convolucionales de grafos?
3) Se utilizan ampliamente en Google, que es probablemente la empresa de IA más sofisticada del mundo, para una amplia gama de tareas, a pesar de la existencia de métodos más complejos y de última generación.
Más lecturas
- El Perceptrón: A Probabilistic Model for Information Storage and Organization in the Brain, Cornell Aeronautical Laboratory, Psychological Review, por Frank Rosenblatt, 1958 (PDF)
- A Logical Calculus of Ideas Immanent in Nervous Activity, W. S. McCulloch & Walter Pitts, 1943
- Perceptrons: Una introducción a la geometría computacional, por Marvin Minsky & Seymour Papert
- Multi-capas (MLP)
- Teoría hebbiana
Otros posts de la Wiki de Pathmind
- Redes neuronales profundas
- Redes neuronales recurrentes Networks (RNNs) and LSTMs
- Word2vec and Neural Word Embeddings
- Convolutional Neural Networks (CNNs) and Image Processing
- Accuracy, Precision and Recall
- Attention Mechanisms and Transformers
- Eigenvectors, Eigenvalues, PCA, Covariance and Entropy
- Graph Analytics and Deep Learning
- Symbolic Reasoning and Machine Learning
- Markov Chain Monte Carlo, AI and Markov Blankets
- Deep Reinforcement Learning
- Generative Adversarial Networks (GANs)
- AI vs Machine Learning vs Deep Learning