Vuelve al índice de lecciones | Haz las lecciones en orden | Página para imprimir
El teorema del factor
El teorema del factor es un resultado del teorema del resto, y se basa en el mismo razonamiento. Si no has leído la lección sobre el Teorema del Resto, repasa primero ese tema y luego vuelve aquí.
Como señala el Teorema del Resto, si divides un polinomio p(x) por un factor x – a de ese polinomio, entonces obtendrás un resto cero. Veamos de nuevo esa expresión del Algoritmo de la División del polinomio:
Publicidad
P(x) = (x – a)q(x) + r(x)
Si x – a es efectivamente un factor de p(x), entonces el resto tras la división por x – a será cero. Es decir:
- Usa el Teorema del Factor para determinar si x – 1 es un factor de
f (x) = 2×4 + 3×2 – 5x + 7. - Usando el Teorema del Factor, verifica que x + 4 es un factor de
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16. - Utilizando el hecho de que -2 y 1/3 son ceros de f (x) = 3×4 + 5×3 + x2 + 5x – 2, factoriza el polinomio completamente. Copyright © Elizabeth Stapel 2002-2011 Todos los derechos reservados
p(x) = (x – a)q(x)
En términos del Teorema del Resto, esto significa que, si x – a es un factor de p(x), entonces el resto, cuando hagamos la división sintética por
x = a, será cero.
El punto del Teorema del Factor es el inverso del Teorema del Resto: Si se divide sintéticamente un polinomio por x = a y se obtiene un resto cero, entonces, no sólo x = a es un cero del polinomio (cortesía del Teorema del Resto), sino que x – a es también un factor del polinomio (cortesía del Teorema del Factor).
Al igual que con el Teorema del Resto, el punto aquí es no hacer la división larga de un polinomio dado por un factor dado. Este Teorema no está repitiendo lo que ya sabes, sino que intenta hacerte la vida más sencilla. Cuando te enfrentes a un ejercicio del Teorema del Factor, aplicarás la división sintética y luego comprobarás si el resto es cero.
Para que x – 1 sea un factor de f (x) = 2×4 + 3×2 – 5x + 7, el Teorema del Factor dice que x = 1 debe ser un cero de f (x). Para comprobar si x – 1 es un factor, primero fijaré x – 1 igual a cero y resolveré para encontrar el cero propuesto, x = 1. A continuación, utilizaré la división sintética para dividir f (x) entre x = 1. Como no hay ningún término cúbico, tendré cuidado de recordar que debo insertar un «0» en la primera línea de la división sintética para representar la potencia omitida de x en 2×4 + 3×2 – 5x + 7:
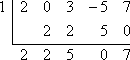
Como el resto no es cero, entonces el Teorema del Factor dice que:
x – 1 no es un factor de f (x).
Si x + 4 es un factor, entonces (poniendo este factor igual a cero y resolviendo) x = -4 es una raíz. Para hacer la comprobación requerida, necesito comprobar que, cuando uso la división sintética en f (x), con x = -4, obtengo un resto cero:
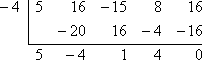
El resto es cero, por lo que el Teorema del Factor dice que:
x + 4 es un factor de 5×4 + 16×3 – 15×2 + 8x + 16.
En la práctica, el Teorema del Factor se utiliza cuando se factorizan polinomios «completamente». En lugar de probar varios factores utilizando la división larga, se utilizará la división sintética y el Teorema del Factor. Cada vez que se divide por un número (siendo una raíz potencial del polinomio) y se obtiene un resto cero en la división sintética, esto significa que el número es efectivamente una raíz, y por lo tanto «x menos el número» es un factor. Entonces continuarás la división con el polinomio más pequeño resultante, continuando hasta llegar a un factor lineal (con lo que habrás encontrado todos los factores) o cuadrático (al que podrás aplicar la Fórmula Cuadrática).
Si x = -2 es un cero, entonces x + 2 = 0, por lo que x + 2 es un factor. Del mismo modo, si x = 1/3 es un cero, entonces x – 1/3 = 0, por lo que x – 1/3 es un factor. Al darme dos de los ceros, también me han dado dos factores: x + 2 y x – 1/3.
Como he empezado con un polinomio de cuarto grado, entonces me quedará una cuadrática una vez que divida estos dos factores dados. Puedo resolver esa cuadrática usando la Fórmula Cuadrática o algún otro método.
El Teorema del Factor dice que no tengo que hacer la división larga con los factores conocidos de x + 2 y x – 1/3. En su lugar, puedo utilizar la división sintética con los ceros asociados -2 y 1/3. Esto es lo que obtengo cuando hago la primera división con x = -2:
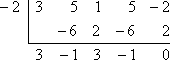
El resto es cero, lo cual es esperable porque me habían dicho al principio que -2 era un cero conocido del polinomio. En lugar de volver a empezar con el polinomio original, ahora trabajaré con el factor del polinomio restante de 3×3 – x2 + 3x – 1 (de la línea inferior de la división sintética). Lo dividiré por el otro cero dado, x = 1/3:
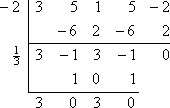
Esto me deja la cuadrática 3×2 + 3, que puedo resolver:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Si los ceros son x = -i y x = i, entonces los factores son x – (-i) y x – (i), o x + i y x – i. I need to remember that I divided off a «3» when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. «The Factor Theorem.» Purplemath. Available from 2016
|