Ventajas de la utilización de variables instrumentales para demostrar la causalidad
Como ejemplo, considere la cuestión de la estimación del efecto de la educación sobre los ingresos. La técnica de estimación más sencilla, los mínimos cuadrados ordinarios (MCO), genera estimaciones que indican que un año adicional de educación se asocia a unos ingresos entre un 6 y un 10% superiores. Sin embargo, la relación positiva puede deberse a la autoselección en la educación; es decir, los individuos que tienen más que ganar con una mayor educación tienen más probabilidades de quedarse. Este será el caso, por ejemplo, si a los alumnos con mayor capacidad les resulta más fácil estudiar y, de todos modos, es probable que reciban salarios más altos. Por lo tanto, la correlación positiva observada entre los años de educación y los salarios reflejaría en parte la prima por capacidad, y no podría interpretarse como el rendimiento de un año adicional de educación, como se pretende. Por lo tanto, las estimaciones OLS no serían informativas sobre el efecto de una política diseñada para aumentar los años de educación. Este problema se denomina «sesgo de variable omitida». Se produce cuando una variable (como la capacidad) que no es observada por el investigador está correlacionada tanto con el tratamiento (más educación) como con el resultado (ingresos). La dirección (sobreestimación o subestimación) y el tamaño del sesgo en las estimaciones OLS es una función del signo y la fuerza de las correlaciones.
En este ejemplo, un ensayo de control aleatorio (RCT), que implicaría la asignación de la educación al azar a los individuos y la observación de las diferencias en sus salarios a lo largo de su vida, es simplemente inviable por razones éticas. Sin embargo, algunos experimentos naturales o cuasi-naturales pueden acercarse a la alteración de la elección educativa de algunos grupos de individuos y, como tales, pueden utilizarse como instrumentos. Uno de estos experimentos naturales es la modificación de la edad mínima legal para abandonar la escuela (edad de finalización de los estudios). Este tipo de cambio afecta a todos los alumnos, independientemente de su capacidad. Por lo tanto, actúa como un choque externo en el que no puede influir el alumno individual.
Muchos países tienen una legislación que estipula la edad a la que los alumnos pueden abandonar el sistema educativo. Por ejemplo, digamos que un niño puede dejar la escuela el último día del año escolar si tiene 14 años a finales de agosto. Supongamos ahora que la legislación se modifica, de modo que los niños tienen que tener 15 años a finales de agosto para poder dejar la escuela. Los niños que querían dejar la escuela a los 14 años no pueden hacerlo y tienen que permanecer un año más de escolarización. Bajo el supuesto (fuerte) de que los niños bajo las dos legislaciones son similares y se enfrentan a condiciones similares del mercado laboral, el cambio de legislación crea un experimento cuasi-natural: independientemente de su capacidad, algunos individuos se verán afectados por el cambio en la edad de abandono escolar y tendrán que permanecer durante un año adicional de escolarización, mientras que los alumnos con preferencias similares de la cohorte anterior no lo harán. Si los investigadores supieran quiénes querían dejar la escuela a los 14 años, podrían comparar los resultados de los individuos que dejaron la escuela a los 14 años con los resultados de los individuos que se vieron obligados a permanecer hasta los 15 años. Esta simple diferencia sería entonces el efecto causal de permanecer en la escuela entre los 14 y los 15 años. Desgraciadamente, los datos observacionales no nos permiten identificar a los individuos cuya elección educativa se vio afectada por la reforma; así, con la nueva legislación, los individuos que querían dejar la escuela a los 15 años son indistinguibles de los que querían dejarla a los 14 pero tuvieron que permanecer un año más. No obstante, lo que hace la reforma es alterar la probabilidad de permanecer en la escuela y, por lo tanto, puede utilizarse como instrumento, ya que afecta a la probabilidad del tratamiento (otro año de escolarización) sin afectar al resultado de interés (por ejemplo, los ingresos).
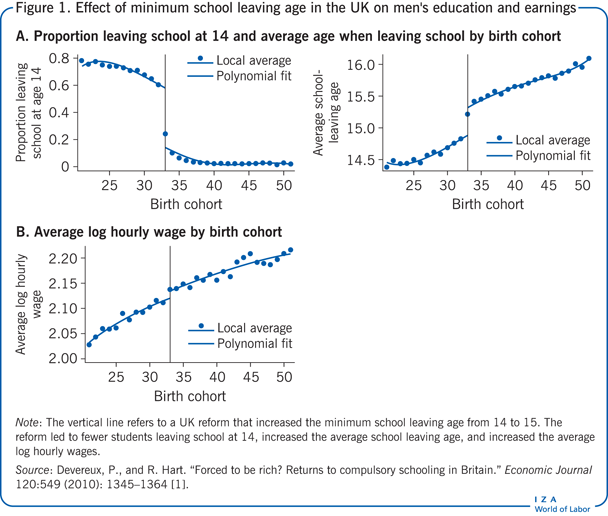
En 1947, un cambio legislativo en el Reino Unido aumentó la edad mínima para dejar la escuela de 14 a 15 años, afectando a los niños nacidos en 1933 y después. Este cambio en la ley ofrece la oportunidad de evaluar el efecto de la escolarización (adicional) sobre los ingresos . En la Figura 1, el panel A muestra que la reforma afectó tanto a la fracción de niños que abandonaron la escuela en la primera oportunidad (gráfico de la izquierda) como a la cantidad total de escolarización completada (gráfico de la derecha). Las estimaciones indican que la reforma aumentó los años medios de escolarización de los hombres en 0,397 años. Esta estimación del efecto de la reforma (el IV) sobre el tratamiento (la educación) se conoce como «regresión de primera etapa». Si la educación tiene algún efecto causal sobre los ingresos, deberíamos observar que los ingresos medios de los individuos afectados por la reforma son también mayores. Este es efectivamente el caso, como se muestra en el panel B de la Figura 1, que informa de los ingresos medios de los hombres. Esta serie muestra una clara ruptura en 1933, cuya magnitud implica que los individuos afectados por la reforma ganan, por término medio, un 1,2% más de salario. Esta segunda estimación del efecto de la reforma (el IV) sobre el resultado (los ingresos) se conoce como «estimación de forma reducida». Una estrategia de IV simple, en este caso utilizando un instrumento binario que toma sólo dos valores (1 para ser afectado por la reforma, y 0 para no ser afectado por la reforma), es el ratio de la estimación de forma reducida sobre la estimación de la primera etapa. (En este caso, el efecto causal de la educación adicional sobre los ingresos sería de 0,012/0,397 = 0,030 y, por tanto, de aproximadamente el 3%.
La intuición de este enfoque es que el efecto de un año más de educación sobre los salarios es básicamente el efecto de la reforma (el IV) sobre los salarios (el resultado) -que se da en la forma reducida- escalado por el efecto que la reforma tiene sobre los años de educación (el tratamiento) -que es de lo que trata la estimación de la primera etapa-. Si el instrumento es «relevante», es decir, tiene un efecto sobre la educación (el tratamiento), y si el instrumento afecta a los salarios «exclusivamente» a través de su efecto sobre la educación, entonces las estimaciones IV pueden interpretarse como el efecto causal del tratamiento sobre el resultado. Estas dos condiciones se denominan «relevancia del instrumento» y «restricción de exclusión».
Para resumir, cuando una variable no observada como la capacidad se correlaciona tanto con el tratamiento como con el resultado, una estimación simple como la de MCO estará sesgada debido a la autoselección en el tratamiento. Del mismo modo, si la variable de tratamiento se mide con error, la estimación MCO estará sesgada hacia cero. Sin embargo, se puede recuperar una estimación causal de un tratamiento sobre un resultado si se encuentra un instrumento creíble. Un instrumento creíble debe satisfacer dos condiciones:
- Relevancia: el instrumento debe afectar a la probabilidad de tratamiento. En una regresión del tratamiento sobre el instrumento, también conocida como ecuación de primera etapa, el coeficiente sobre el IV debe ser suficientemente fuerte.
-
Restricción de exclusión: el instrumento afecta al resultado exclusivamente a través de su efecto sobre el tratamiento.
Si se puede encontrar dicho IV (es decir. se cumplen tanto la relevancia como la restricción de exclusión), entonces se puede implementar una estrategia de IV para recuperar un efecto causal del tratamiento sobre el resultado.
El ejemplo anterior presentaba la estimación de Wald, es decir, el cociente de las estimaciones de dos regresiones: la estimación de forma reducida, procedente de una regresión del resultado sobre el instrumento; y la estimación de la primera etapa, procedente de una regresión del tratamiento sobre el instrumento. Esto puede calcularse fácilmente cuando el instrumento sólo toma dos valores. En el caso más general, se calculará una estimación de «mínimos cuadrados de dos etapas» (2SLS), en la que las predicciones del tratamiento de la ecuación de la primera etapa se utilizan en una regresión del resultado sobre el tratamiento, en lugar del valor real del tratamiento. De este modo, sólo la variación del tratamiento procedente del instrumento se utiliza para explicar la varianza del resultado. Esto resuelve el sesgo de autoselección. En el caso de un instrumento binario (de dos valores), las estimaciones Wald y 2SLS serán idénticas (véase , por ejemplo). Sin embargo, la dificultad no radica en la implementación de dicha estimación 2SLS, ya que todos los paquetes estadísticos pueden calcular estimaciones IV, sino en (a) encontrar un instrumento válido y (b) interpretar los resultados. La discusión se centrará ahora en estos dos puntos.