Vitesse d’une onde sur une corde tendue
Pour voir comment la vitesse d’une onde sur une corde dépend de la tension et de la densité linéaire, considérons une impulsion envoyée le long d’une corde tendue (Figure \(\PageIndex{1}\)). Lorsque la corde tendue est au repos à la position d’équilibre, la tension dans la corde \(F_T\) est constante. Considérons un petit élément de la corde dont la masse est égale à \(\Delta m = \mu \Delta x\). L’élément de masse est au repos et en équilibre et la force de tension de chaque côté de l’élément de masse est égale et opposée.
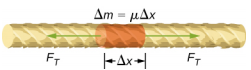
Si l’on pince une corde sous tension, une onde transversale se déplace dans la direction x positive, comme le montre la figure \(\PageIndex{2}\). L’élément de masse est petit mais il est agrandi sur la figure pour le rendre visible. Le petit élément de masse oscille perpendiculairement au mouvement de l’onde en raison de la force de rappel fournie par la corde et ne se déplace pas dans la direction x. La tension FT dans la ficelle, qui agit dans la direction x positive et négative, est approximativement constante et est indépendante de la position et du temps.
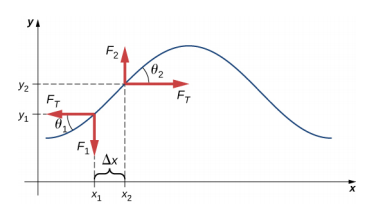
Supposons que l’inclinaison de la corde déplacée par rapport à l’axe horizontal est faible. La force nette sur l’élément de la corde, agissant parallèlement à la corde, est la somme de la tension de la corde et de la force de rappel. Les composantes x de la force de tension s’annulent, de sorte que la force nette est égale à la somme des composantes y de la force. L’amplitude de la composante x de la force est égale à la force de tension horizontale de la corde \(F_T\) comme illustré sur la figure \(\PageIndex{2}\). Pour obtenir les composantes y de la force, notez que tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}\) et \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}\). Le \(\tan \theta\) est égal à la pente d’une fonction en un point, qui est égale à la dérivée partielle de y par rapport à x en ce point. Ainsi, \(\frac{F_{1}}{F_{T}}\) est égal à la pente négative de la corde en x1 et \(\frac{F_{2}}{F_{T}}\) est égal à la pente de la corde en x2 :
La force nette est sur l’élément de petite masse peut s’écrire comme
\ \ldotp\]
En utilisant la deuxième loi de Newton, la force nette est égale à la masse multipliée par l’accélération. La densité linéaire de la corde µ est la masse par longueur de la corde, et la masse de la portion de la corde est \(\mu \Delta\)x,
\N{\i1}Ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\right) \ldotp\]
Diviser par FT\(\Delta\)x et prendre la limite lorsque \(\Delta\)x s’approche de zéro,
{\i1}{\i1}-{\i1}& = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}}
Rappelle-toi que l’équation linéaire des ondes est
Donc,
En résolvant pour \(v\), on voit que la vitesse de l’onde sur une corde dépend de la tension et de la densité linéaire
Vitesse d’une onde sur une corde sous tension
La vitesse d’une impulsion ou d’une onde sur une corde sous tension peut être trouvée avec l’équation
où \(F_T\) est la tension dans la corde et \(µ\) est la masse par longueur de la corde.
Sur une guitare à six cordes, la corde de mi aigu a une densité linéaire de \(\mu_{High\ ; E}\) = 3,09 x 10-4 kg/m et la corde de mi grave a une densité linéaire de \(\mu_{Low\ ; E}\) = 5,78 x 10-3 kg/m. (a) Si la corde de Mi élevé est pincée, produisant une onde dans la corde, quelle est la vitesse de l’onde si la tension de la corde est de 56,40 N ? (b) La densité linéaire de la corde de mi grave est environ 20 fois supérieure à celle de la corde de mi aigu. Pour que les ondes se propagent à travers la corde à faible indice d’octave à la même vitesse que la corde à fort indice d’octave, la tension doit-elle être plus grande ou plus petite que celle de la corde à fort indice d’octave ? Quelle serait la tension approximative ? (c) Calculez la tension de la corde à faible E nécessaire pour obtenir la même vitesse d’onde.
Stratégie
- La vitesse de l’onde peut être trouvée à partir de la densité linéaire et de la tension \(v = \sqrt{\frac{F_{T}}{\mu}\).
- D’après l’équation v = \(\sqrt{\frac{F_{T}}{\mu}}\), si la densité linéaire est augmentée d’un facteur de presque 20, la tension devrait être augmentée d’un facteur 20.
- Connaissant la vitesse et la densité linéaire, l’équation de la vitesse peut être résolue pour la force de tension FT = \(\mu\)v2.
Solution
- Utiliser l’équation de vitesse pour trouver la vitesse : $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\ ; N}{3,09 \times 10^{-4}\ ; kg/m}} = 427,23\ ; m/s \ldotp$$
- La tension devrait être augmentée d’un facteur d’environ 20. La tension serait légèrement inférieure à 1128 N.
- Utiliser l’équation de la vitesse pour trouver la tension réelle : $$F_{T} = \mu v^{2} = (5,78 \times 10^{-3}\ ; kg/m)(427,23\ ; m/s)^{2} = 1055,00\ ; N \ldotp$$
- Cette solution est à moins de 7% de l’approximation.
Signification
Les notes standard de la six cordes (mi aigu, si, sol, ré, la, mi grave) sont accordées pour vibrer aux fréquences fondamentales (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz et 82,41 Hz) lorsqu’elles sont pincées. Les fréquences dépendent de la vitesse des ondes sur la corde et de la longueur d’onde des ondes. Les six cordes ont des densités linéaires différentes et sont « accordées » en modifiant les tensions des cordes. Nous verrons dans Interférence des ondes que la longueur d’onde dépend de la longueur des cordes et des conditions aux limites. Pour jouer des notes autres que les notes fondamentales, on modifie la longueur des cordes en appuyant dessus.
Exercice 16.5
La vitesse d’une onde sur une corde dépend de la tension et de la densité linéaire de masse. Si l’on double la tension, que se passe-t-il pour la vitesse des ondes sur la corde ?
.