Hullámsebesség feszített húron
Hogy lássuk, hogyan függ a hullám sebessége egy húron a feszültségtől és a lineáris sűrűségtől, tekintsünk egy feszített húron lefelé küldött impulzust (\(\PageIndex{1}\) ábra). Amikor a megfeszített húr nyugalmi helyzetben van az egyensúlyi helyzetben, a húr \(F_T\) feszültsége állandó. Tekintsük a húr egy kis elemét, amelynek tömege \(\Delta m = \mu \Delta x\). A tömegelem nyugalomban és egyensúlyban van, és a tömegelem mindkét oldalának feszítőereje egyenlő és ellentétes.
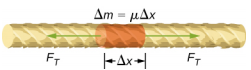
Ha egy feszített húrt megrántunk, egy keresztirányú hullám mozog a pozitív x irányban, ahogy az \(\PageIndex{2}\) ábrán látható. A tömegelem kicsi, de az ábrán felnagyítottuk, hogy látható legyen. A kis tömegelem a húr által kifejtett visszaállító erő hatására a hullámmozgásra merőlegesen rezeg, és nem mozog az x irányban. A húrban a pozitív és negatív x-irányban ható FT feszültség megközelítőleg állandó, és független a helyzettől és az időtől.
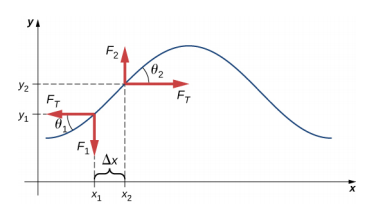
Tegyük fel, hogy az elmozdult húr dőlése a vízszintes tengelyhez képest kicsi. A húr elemére ható, a húrral párhuzamosan ható nettó erő a húrban lévő feszültség és a visszaállító erő összege. A feszítőerő x-összetevői kioltják egymást, így a nettó erő egyenlő az erő y-összetevőinek összegével. Az erő x-komponensének nagysága megegyezik a húr vízszintes feszítő erejével \(F_T\), ahogy az \(\PageIndex{2}\) ábrán látható. Az erő y-komponensének kiszámításához vegyük figyelembe, hogy tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}}\) és \(\tan \theta_{2} = \frac{F_{2}}}{F_{T}}}\). Az \(\tan \theta\) egyenlő a függvény meredekségével egy pontban, ami egyenlő az y parciális deriváltjával az adott pont x-hez viszonyítva. Ezért \(\frac{F_{1}}{F_{T}}}\) egyenlő a húr negatív meredekségével az x1 pontban, \(\frac{F_{2}}{F_{T}}}\) pedig egyenlő a húr meredekségével az x2 pontban:
\\
A kis tömegű elemre ható nettó erő a következőképpen írható fel:
\ \ldotp\]
Newton második törvényét alkalmazva a nettó erő egyenlő a tömeg és a gyorsulás szorzatával. A húr µ lineáris sűrűsége a húr hosszára eső tömeg, a húr egy részének tömege pedig \(\mu \Delta\)x,
\ = \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}}}\right) \ldotp\]
Elosztva FT\(\Delta\)x-szel és a határértéket véve \(\Delta\)x nullához közelítve,
\}{\Delta x} & = \frac{\\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\ \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]
Megjegyezzük, hogy a lineáris hullámegyenlet
\
Ezért,
\
feloldva \(v\), azt látjuk, hogy a hullám sebessége egy húron a feszültségtől és a lineáris sűrűségtől függ
A hullám sebessége egy húron feszültség alatt
A hullám sebessége egy húron feszültség alatt a következő egyenlet segítségével állapítható meg
\
ahol \(F_T\) a húron lévő feszültség és \(µ\) a húr hosszára eső tömeg.
16.5. példa: Egy gitárrugó hullámsebessége
Egy hathúros gitáron a magas E húr lineáris sűrűsége \(\mu_{High\; E}\) = 3,09 x 10-4 kg/m, a mély E húr lineáris sűrűsége pedig \(\mu_{Low\; E}\) = 5,78 x 10-3 kg/m. (a) Ha a magas E húr megpengetésével a húrban hullám keletkezik, mekkora a hullám sebessége, ha a húr feszültsége 56,40 N? (b) Az alacsony E húr lineáris sűrűsége körülbelül 20-szor nagyobb, mint a magas E húré. Ahhoz, hogy a hullámok az alacsony E húrban ugyanolyan hullámsebességgel haladjanak, mint a magas E húrban, nagyobb vagy kisebb feszültségnek kell lennie, mint a magas E húrban? Mekkora lenne a hozzávetőleges feszültség? (c) Számítsa ki az alacsony E húr feszültségét, amely ugyanahhoz a hullámsebességhez szükséges.
Stratégia
- A hullám sebessége a lineáris sűrűségből és a \(v = \sqrt{\sqrt{\frac{F_{T}}{\mu}}\) feszültségből állapítható meg.
- A v = \(\sqrt{\frac{F_{T}}}{\mu}}\) egyenletből, ha a lineáris sűrűséget közel 20-szorosára növeljük, akkor a feszültséget is 20-szorosára kellene növelni.
- A sebesség és a lineáris sűrűség ismeretében a sebességegyenlet megoldható a feszítőerőre FT = \(\mu\)v2.
megoldás
- A sebességegyenletet használjuk a sebesség meghatározásához: $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\; N}{3.09 \times 10^{-4}\; kg/m}} = 427.23\; m/s \ldotp$$
- A feszültséget körülbelül 20-szorosára kell növelni. A feszültség valamivel kevesebb lenne, mint 1128 N.
- A sebességegyenletet használjuk a tényleges feszültség meghatározásához: $$$F_{T} = \mu v^{2} = (5.78 \times 10^{-3}\; kg/m)(427.23\; m/s)^{2} = 1055.00\; N \ldotp$$
- Ez a megoldás a közelítés 7%-án belül van.
Szignifikancia
A hat húr standard hangjai (magas E, H, G, D, A, mély E) úgy vannak hangolva, hogy pengetéskor az alapfrekvenciákon (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz és 82,41 Hz) rezegjenek. A frekvenciák a húr hullámsebességétől és a hullámok hullámhosszától függnek. A hat húr különböző lineáris sűrűségű, és a húrok feszültségének változtatásával “hangolható”. A Hullámok interferenciája című fejezetben látni fogjuk, hogy a hullámhossz a húrok hosszától és a peremfeltételektől függ. Az alaphangoktól eltérő hangok lejátszásához a húrok hosszát a húrok lenyomásával változtatjuk.
GYakorlat 16.5
A húrra felhúzott hullám sebessége a feszültségtől és a lineáris tömegsűrűségtől függ. Ha a feszültséget megduplázzuk, mi történik a hullámok sebességével a húron?