Velocità dell’onda su una corda sotto tensione
Per vedere come la velocità di un’onda su una corda dipende dalla tensione e dalla densità lineare, consideriamo un impulso inviato lungo una corda tesa (Figura \PageIndex{1}}). Quando la corda tesa è a riposo nella posizione di equilibrio, la tensione nella corda \(F_T\) è costante. Consideriamo un piccolo elemento della corda con una massa pari a \(\Delta m = \mu \Delta x\). L’elemento di massa è a riposo e in equilibrio e la forza di tensione di entrambi i lati dell’elemento di massa è uguale e opposta.
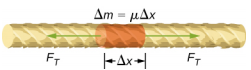
Se si pizzica una corda sotto tensione, un’onda trasversale si muove nella direzione x positiva, come mostrato nella figura \(\PageIndex{2}}. L’elemento di massa è piccolo ma è ingrandito nella figura per renderlo visibile. Il piccolo elemento di massa oscilla perpendicolarmente al moto dell’onda come risultato della forza di ripristino fornita dalla corda e non si muove nella direzione x. La tensione FT nella corda, che agisce in direzione x positiva e negativa, è approssimativamente costante ed è indipendente dalla posizione e dal tempo.
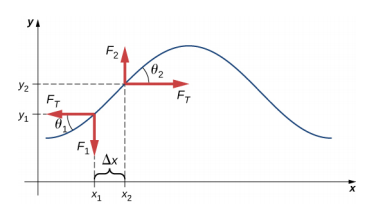
Assumiamo che l’inclinazione della corda spostata rispetto all’asse orizzontale sia piccola. La forza netta sull’elemento della corda, che agisce parallelamente alla corda, è la somma della tensione della corda e della forza di ripristino. I componenti x della forza di tensione si annullano, quindi la forza netta è uguale alla somma dei componenti y della forza. La grandezza della componente x della forza è uguale alla forza orizzontale di tensione della corda \(F_T\) come mostrato nella figura \(\PageIndex{2}}). Per ottenere i componenti y della forza, si noti che tan \(\theta_{1} = – \frac{F_{1}}}) e \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}). Il \(\tan \theta\) è uguale alla pendenza di una funzione in un punto, che è uguale alla derivata parziale di y rispetto a x in quel punto. Quindi, \frac{F_{1}}{F_{T}}} è uguale alla pendenza negativa della corda in x1 e \frac{F_{2}}{F_{T}}} è uguale alla pendenza della corda in x2:
La forza netta è sull’elemento di massa piccola può essere scritta come
\ldotp\]
Utilizzando la seconda legge di Newton, la forza netta è uguale alla massa per l’accelerazione. La densità lineare della corda µ è la massa per lunghezza della corda, e la massa della porzione di corda è \(\mu \Delta\)x,
= \Delta ma = \mu \Delta x \sinistra(\frac{parziale^{2} y}{parziale t^{2}} destra) \ldotp\]
Dividendo per FT(\Delta\)x e prendendo il limite come \(\Delta\)x si avvicina a zero,
{{Delta x} & = \frac{\mu}{F_{T} \frac{parziale^{2} y}{parziale t^{2} \frac \frac \frac \parziale^{2} y}{parziale x^{2} & = \frac{\mu}{F_{T} \frac{parziale^{2} y}{parziale t^{2}
Ricordiamo che l’equazione d’onda lineare è
Quindi,
Solvendo per \(v), vediamo che la velocità dell’onda su una corda dipende dalla tensione e dalla densità lineare
Velocità di un’onda su una corda sotto tensione
La velocità di un impulso o di un’onda su una corda sotto tensione può essere trovata con l’equazione
dove \(F_T\) è la tensione nella corda e \(µ\) è la massa per lunghezza della corda.
Esempio 16.5: La velocità d’onda di una molla di chitarra
Su una chitarra a sei corde, la corda E alta ha una densità lineare di \(\mu_{Alta; E}\) = 3,09 x 10-4 kg/m e la corda E bassa ha una densità lineare di \(\mu_{Bassa; E}\) = 5,78 x 10-3 kg/m. (a) Se la corda ad alta E viene pizzicata, producendo un’onda nella corda, qual è la velocità dell’onda se la tensione della corda è 56,40 N? (b) La densità lineare della corda E bassa è circa 20 volte maggiore di quella della corda E alta. Affinché le onde viaggino attraverso la corda E bassa alla stessa velocità dell’onda della E alta, la tensione dovrebbe essere maggiore o minore di quella della corda E alta? Quale sarebbe la tensione approssimativa? (c) Calcola la tensione della corda a bassa E necessaria per la stessa velocità dell’onda.
Strategia
- La velocità dell’onda può essere trovata dalla densità lineare e dalla tensione \(v = \sqrt{\frac{F_{T}}{\mu}}).
- Dall’equazione v = \(\sqrt{frac{F_{T}}{\mu}}, se la densità lineare è aumentata di un fattore di quasi 20, la tensione dovrebbe essere aumentata di un fattore 20.
- Conoscendo la velocità e la densità lineare, l’equazione della velocità può essere risolta per la forza di tensione FT = \(\mu\)v2.
Soluzione
- Utilizzare l’equazione della velocità per trovare la velocità: $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\; N}{3.09 \times 10^{-4}; kg/m}} = 427.23\; m/s \ldotp$$
- La tensione dovrebbe essere aumentata di un fattore di circa 20. La tensione sarebbe leggermente inferiore a 1128 N.
- Utilizzare l’equazione della velocità per trovare la tensione reale: $$F_{T} = \mu v^{2} = (5.78 \volte 10^{-3}\kg/m)(427.23\; m/s)^{2} = 1055.00\; N \ldotp$$
- Questa soluzione è entro il 7% dell’approssimazione.
Significato
Le note standard delle sei corde (Mi alto, Si, Sol, Re, La, Mi basso) sono accordate per vibrare alle frequenze fondamentali (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz e 82,41 Hz) quando vengono pizzicate. Le frequenze dipendono dalla velocità delle onde sulla corda e dalla lunghezza d’onda delle onde. Le sei corde hanno diverse densità lineari e vengono “accordate” cambiando le tensioni delle corde. Vedremo nell’Interferenza delle Onde che la lunghezza d’onda dipende dalla lunghezza delle corde e dalle condizioni al contorno. Per suonare note diverse da quelle fondamentali, le lunghezze delle corde vengono cambiate premendo sulle corde stesse.
Esercizio 16.5
La velocità di un’onda su una corda dipende dalla tensione e dalla densità lineare della massa. Se la tensione viene raddoppiata, cosa succede alla velocità delle onde sulla corda?