張力のあるひもの波の速さ
ひもの上の波の速さが張力と線密度にどう依存するかを見るために、張力のあるひもにパルスを送ったとします(図㊤)。 張ってある紐が平衡位置で静止しているとき、紐の張力(F_T)は一定である。 このとき、紐の中に質量の等しい小さな要素(ε=ε=ε=ε=ε=ε=)があるとします。
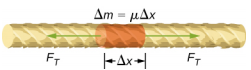
張力のかかった弦を弾くと、図(㊦)のように横波が正のx方向に動きます。 質量要素は小さいのですが、図では見えるように大きくしてあります。 小さな質量要素は弦の復元力により波動に対して垂直に振動し、x方向には移動しない。 x方向の正負に作用する弦の張力FTはほぼ一定で、位置や時間に依存しない。
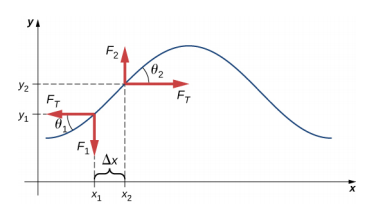
変位した弦の水平軸に対する傾きが小さいと仮定します。 弦と平行に作用する弦の要素にかかる正味の力は、弦の張力と復元力の和である。 張力のx成分は相殺されるので、正味の力は力のy成分の和に等しくなる。 力のx成分の大きさは、図(㊦)のように紐の水平方向の引張力(F_T)と等しくなります。 力のy成分を求めるには、tan Ⓐ= – Ⓐfrac{F_{1}{F_{T}} Ⓑ= Ⓑfrac{F_{2}}{F_{T}} Ⓕ= Ⓑfrac{F_{2}} {F_{1}]とする。) また、ある点での関数の傾きは、その点でのxに対するyの偏微分と等しく、この点での関数の傾きは、その点でのxに対するyの偏微分と等しく、この点での関数の傾きは、その点でのxに対するyの偏微分と等しくなります。 従って、(F_{1}}{F_{T}}はx1における弦の負の傾きに、(F_{2}}{F_{T}}はx2における弦の傾きに等しくなります。
小さな質量要素にかかる正味の力は次のように書くことができます
\ldotp]
ニュートンの第二法則を用いて、正味の力は質量に加速度をかけたものに等しくなります。 紐の線密度μは紐の長さあたりの質量で、紐の部分の質量は୧⃛(๑⃙⃘◡̈๑⃙⃘)୨⃛となります。
Ⓐ= \Delta ma = \mu \Delta x \left(\frac{partial^{2} y}{partial t^{2}}right) \ldotp]
FT(Delta)xで割って、 \(Delta)x approaches zeroで極限をとります。
}{Delta x} & = \frac{Mu}{F_{T}} div \frac{partial^{2} y}{partial t^{2}} \frac{partial^2} y}{partial x^{2}}. & = \frac{mu}{F_{T}}. \frac{partial^{2} y}{partial t^{2}} \ʕ-̫͡-ʔ̫͡-ʔ]
線形波動方程式は
したがって、
Solving for \(v),
Speed of a Wave on a String Under Tension
張力があるときの波の速度は、式
(F_Thesis) is the tension in string and \(μThesis) is the mass per length of stringで求められる。
例題16.5:ギターのバネの波速
6弦ギターにおいて、高E弦の線密度は3.09 x 10-4 kg/m 、低E弦は5.78 x 10-3 kg/mであった。 (a) 高E弦を弾いて弦に波を発生させた場合、弦の張力が56.40Nであれば、波の速さは何Nでしょうか? (b) 低E弦の線密度は高E弦の線密度の約20倍である。 低E弦の中を波が高E弦と同じ波速で伝わるためには、張力は高E弦より大きくする必要があるか、小さくする必要があるか? おおよその張力はどのくらいでしょう? (c) 同じ波速のために必要な低E弦の張力を計算する。
戦略
- 波の速さは線密度と張力から求めることができる♪(v = \sqrt{T}{F_mu}} )。
- 方程式v = \(\sqrt{Chefrac{F_{T}}{mu}}) から、線密度がほぼ20倍になれば、張力も20倍にする必要がある。
- 速度と線密度がわかれば、速度の方程式は張力FT = \(Ⅻmu})v2 について解くことができる。
解答
- 速度の式を使って速度を求める: $$v = \sqrt{}{F_{T}{Tmu}} = \sqrt{Tfrac}{56.40; N}{3.09 \times 10^{-4}}; kg/m}} = 427.23; m/s \ldotp$$
- テンションは約20倍にする必要があります。
- 速度方程式を使用して実際の張力を求めます。 $$F_{T} = \mu v^{2} = (5.78 \times 10^{-3}}; kg/m)(427.23 translated m/s)^{2} = 1055.00; N \ldotp$
- この解は近似値の 7% 以内に収まっています。
意義
6弦の標準音(high E, B, G, D, A, low E)は、弾いたときに基本周波数(329.63 Hz, 246.94 Hz, 196.00 Hz, 146.83 Hz, 110.00 Hz, 82.41 Hz)で振動するよう調律されています。 周波数は、弦にかかる波の速さと波の波長によって決まる。 6本の弦はそれぞれ異なる線密度を持ち、弦の張力を変えることで「調律」される。 波長が弦の長さと境界条件に依存することは、「波の干渉」で見ることができます。 基本音以外の音を出すには、弦を押さえることで弦の長さを変えます。
練習問題 16.5
弦上の波の速さは、張力と線形質量密度に依存します。 張力が2倍になると、弦の上の波の速度はどうなるでしょうか。
演習16.5
張力を2倍にすると、弦の上の波の速度はどうなるでしょうか。