Existem árvores genealógicas e populações onde o princípio do acasalamento pânico é essencialmente quebrado. Normalmente são comunidades pequenas, geográfica ou socialmente relativamente isoladas. Nessas comunidades o acasalamento consanguíneo de várias ordens (um pai – uma criança, um irmão, primos, tio – sobrinha, etc.), pode ser amplamente difundido.
O problema da influência da consanguinidade na população é o importante problema da genética 1. Agora este problema ainda não recebeu a solução final.
Na maioria dos casos a consanguinidade em uma árvore genealógica leva em conta três gerações. São os parentes mais distantes que são levados em conta no acasalamento consanguíneo há primos em segundo grau.
A consanguinidade é levada em consideração com a ajuda do fator consanguinidade.
O fator consanguinidade é a probabilidade de dois alelos serem idênticos pela origem.
Consideremos o método de cálculo do fator consanguinidade em uma árvore genealógica oferecido por Wright 1, 2.
Para o achado do fator consanguinidade é necessário:
encontrar para os descendentes casados todas as formas em uma árvore genealógica que através do ancestral comum conecte esses descendentes.
contar o número de passos (alternâncias de gerações) em cada forma.
Então o fator de consanguinidade é igual:
 ……(1)
……(1)
onde r há número de formas, m1, m2, …. mi- número de passos em cada caminho.
Após novamente notaremos que o número de adendos na soma (1) é igual ao número de caminhos que através dos antepassados comuns conectam o casamento.
Vamos considerar casos concretos de árvores genealógicas, Figura 1. Nesta figura, o quadrado significa um indivíduo masculino o círculo – indivíduo feminino. Linhas pontilhadas e dígitos idênticos especificam possíveis formas em uma árvore genealógica que através do antepassado comum (o homem ou a mulher) conectam os descendentes consanguíneos que se casam. Em alguns sites de formas, Figura 1с, há dois dígitos 1 e 2. Ele especifica que tais sites são os comuns para as várias formas.
O casamento pai – filha é incesto, Figura 1а. O descendente (mulher) está conectado com o ancestral (homem) ali 1 caminho com um passo, ou seja, m = 1. Portanto, há o fator consanguinidade.
Ft = 1/2.2-1 = 1/4
Há um casamento irmão – irmã (irmãos), Figura 1b. Os dígitos especificam o número do caminho. Os números de dígitos idênticos no caminho do homem casado para a mulher é igual ao número de passos.
Deixe que cada descendente que se casou se conecte com o parceiro dois caminhos com dois passos em cada caminho, ou seja, m = 2. Assim, há o fator consanguinidade.
Ft = 1/2.(2-2 + 2-2) = 1/4
O casamento entre primos é mostrado na Figura 1с.
Figure 1. Alguns tipos de consanguinidade em uma árvore genealógica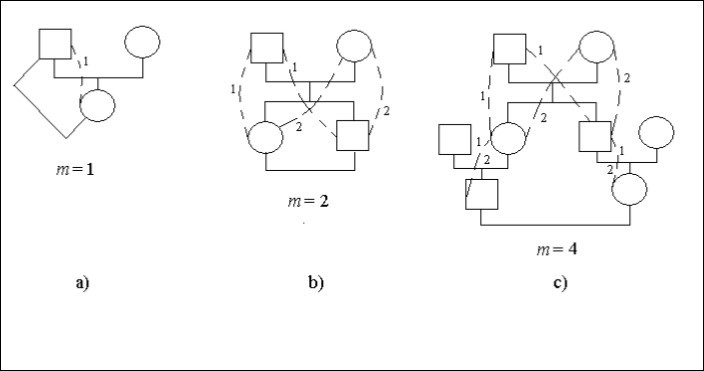
Cada descendente que tenha se casado conecta com o cônjuge os 2 caminhos com 4 passos em cada caminho, ou seja, m = 4. Portanto, há o fator consanguinidade.
Ft = 1/2.(2-4 + 2-4) = 1/16
A fórmula (1) é fácil de entender a partir da seguinte lógica.
Obviamente há 1/2 genes da criança é o comum com cada um dos pais, 1/4 – com o avô e a avó, 1/8 – com o bisavô e a bisavó, etc. Se da mulher para qualquer antepassado liderar o caminho com η passos a partilha dos genes comuns com este antepassado é igual a 2-η. Se do homem para qualquer antepassado leva o caminho com μ passos a parte dos genes comuns é igual 2-μ. No casamento do homem e da mulher com o ancestral comum a cota dos genes comuns com este ancestral será de 2-η. 2-μ = 2-m onde m = η + μ há um número total de passos através do antepassado comum desde a mulher até o homem se casar. O tamanho 1/2 2-m mostra a probabilidade de que o gene casualmente escolhido na mulher será idêntico, por origem, ao gene casualmente escolhido no homem. O mesmo tamanho dá a contribuição para o fator consanguinidade Ft um caminho através do ancestral comum desde a mulher até o homem se casando.
Por exemplo, se o ancestral comum estiver longe de se casar em η = μ = 5 gerações a probabilidade de eles terem o gene comum é igual. 1/2 2-(5+5) = 1/2048 Este tamanho na análise do acasalamento pode ser negligenciado. (Tabela 1)
Tabela 1.inbreeding factors for the some consanguineous marriages are shown in addition.
| O tipo de consanguinidade casamento | |
| Segundo primo | 1/32 |
| Tio primo – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: a origem de alelos idênticos em autossomos homólogos é não consanguínea (a probabilidade desta hipótese é P(H1) = 1- Ft ) e surge homozygoteаа (a probabilidade condicional deste evento é P(aa/H1) = q2) ou a origem de alelos idênticos é consanguínea (a probabilidade desta hipótese é P(H2) = Ft ) e surge homozygoteаа (a probabilidade condicional deste evento é P(aa/H2) = q). A probabilidade q da ocorrência do homozigoto aa no último caso é determinada por que se o alelo a está em um autossomo então na origem consanguínea do homozigoto o mesmo alelo necessariamente deve estar e no autossomo homólogo.
Hence, a probabilidade total da ocorrência recessiva do homozigoto é igual:
 ……….(3)
……….(3)
onde se leva em conta p = 1 – q existe o alelo dominante uma freqüência.
Simplesmente existe a probabilidade total da ocorrência do homozigoto AA dominante no acasalamento aleatório:
 ……….. (4)
……….. (4)
Assim, de acordo com (3) e (4) a frequência total de homozigotos (dominantes e recessivos) na árvore genealógica inbred aumenta em 2Ftpq. Assim, a frequência dos heterozigotos diminui para o mesmo tamanho e para se tornar igual 2pq – 2pqFt = 2pq(1-Ft) já que a soma de todas as frequências dos zigotos é igual a 1.
Em vista do fator de consanguinidade e também (3) e (4) a lei Hardy – Weinberg na geração seguinte de árvore genealógica consanguínea para um genoma autossômico precisa ser escrita as distribuições dos genótipos zigotos como 4:
 …………(5)
…………(5)
Onde pn é o alelo dominante Uma freqüência na geração n, qn – o alelo recessivo uma freqüência, então pn + qn = 1.
A razão (5) refere-se também à razão de Wright 5. A razão de Wright mostra que em uma árvore genealógica consanguínea após o acasalamento consanguíneo dos indivíduos são observados os seguintes efeitos: há aumento da fração homozigotos autossômica em uma árvore genealógica em Ft pnqn e redução da fração heterozigótica autossômica em (1-F1) em comparação com uma população panmítica.
Mas já através de uma geração é restaurado o equilíbrio Hardy – Weinberg que especifica a pequena importância do acasalamento consanguíneo separado para uma árvore genealógica:
 ………(6)
………(6)
Obviamente, para uma população como um todo, o ato separado do acasalamento consanguíneo terá ainda menor importância do que para uma árvore genealógica.
O mesmo efeito da variação da frequência dos genótipos zigoto é observado e para os genes ligados ao sexo.
Distribuição dos genótipos ligados ao cromossoma Х na árvore genealógica panmítica é descrita pela lei de Hardy – Weinberg como 1:
 ………..(7)
………..(7)
A frequência de um alelo dominante A que designaremos no pf masculino pm e no pf feminino. Para alelos recessivos é em conformidade qm e qf .
No acasalamento existe uma proporção de genótipos nas mulheres de acordo com o produto (pf + qf) (pm +qm).
Vamos encontrar a probabilidade total da ocorrência do homozigoto recessivo aa no acasalamento aleatório para os genes da filha ligados ao cromossoma theХ sob a fórmula (2). A lógica dos eventos é semelhante ao caso dos autossomas, exceto que a probabilidade condicional de ocorrência de um genotypeаа a partir dos alelos não consanguíneos de acordo com (7) é igual a P(aa/H1) = qmnqfn. Para os alelos consanguíneos a probabilidade condicional de uma ocorrência de genotypeаа é igual a P(aa/H2) = qf(n+1). Nas filhas, isto é, na geração n+1 a probabilidade de ocorrência de um homozigoto aa é determinada por que se o alelo a está em um cromossomo Х então na origem consanguínea do homozigoto o mesmo alelo necessariamente deve estar e no homozigoto Х.
Hence, a probabilidade total da ocorrência recessiva do homozigoto é igual:
 ……(8)
……(8)
onde pmn é o alelo dominante A frequência na geração n em homens e pfn – em mulheres. Para os alelos recessivos a correspondente qmn e qfn . Além disso é usado qmn =1 – qmn e pfn = 1 – qfn.
encontrando a probabilidade total da ocorrência do homozigoto dominante com o uso:
 ,
,
 ……….(9)
……….(9)
e um heterozigoto P(Aa) = 1- P(aa) – P(AA) – P(AA) encontraremos a distribuição dos genótipos em Х – cromossomas da árvore genealógica consanguínea no acasalamento:
 ……..(10)
……..(10)
É demonstrado simultaneamente que, assim como nos autossomos, os aditivos inatos nas frequências dos homozigotos dominantes e recessivos nos cromossomos ligados ao sexo são idênticos.
Outra forma da razão (10) consistirá no seguinte.
Vamos encontrar primeiro a probabilidade total de ocorrência de um heterozigoto Aa, isto é, P(Aa) na oportunidade do acasalamento consanguíneo aleatório. Esta probabilidade decorre da seguinte lógica de acasalamento: a origem dos alelos é não consanguínea (a probabilidade desta hipótese é P(H1) = 1 – Ft ) também surge heterozigoto Aа (a probabilidade condicional deste evento é P(Aa/H1) = pmnqfn + pfnqmn, ver a fórmula (7)) ou origem dos alelos é consanguínea (a probabilidade desta hipótese é P(H2) = Ft) e surge heterozigoto Aа (a probabilidade condicional deste evento é igual a zero P(Aa/H2) = 0 ). A última afirmação é definida por que na origem consanguínea alelos semelhantes em homólogos Х-cromossomas não podem surgir heterozygoteАа consistindo em alelos diferentes.
Hence, usando a fórmula de probabilidade total encontramos probabilidade total da ocorrência do heterozigoto Aa:
 ……..(11)
……..(11)
Redução de uma frequência heterozigotos Aa ocorre como foi provado anteriormente devido ao aumento idêntico do AA dominante e da frequência aa homozigotos recessiva. Por exemplo, o aumento da frequência de aa homozigotos recessivos é igual:
 ……..(12)
……..(12)
onde a redução da frequência de aa homozigotos recessivos da árvore genealógica panmítica de acordo com (7) e (11) é igual. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) Usando (11) e (12) para atualizar (7) para casos de consanguinidade, encontramos a distribuição dos genótipos (10) em Х-cromossomos nas filhas da árvore genealógica consanguínea.
Na geração seguinte a frequência dos alelos recessivos a nas mulheres é igual:
 ……..(13)
……..(13)
Que obedece totalmente à mesma frequência na ausência de consanguinidade, ou seja, há restauração do equilíbrio Hardy – Weinberg ou é uma abordagem mais exata do equilíbrio.
A relação (7) e (13) mostra como um todo as frequências dos alelos em uma árvore genealógica para o relato da consanguinidade não variam. Há apenas uma redistribuição de alelos. Uma parte dos alelos deixa os heterozigotos e passa para os homozigotos.