MATEMÁTICA Islâmica

>p>>>/p>br>>p>>alguns exemplos das complexas simetrias usadas na decoração de templos islâmicosbr>>p> O Império Islâmico estabelecido em toda a Pérsia, Médio Oriente, Ásia Central, Norte de África, Península Ibérica e partes da Índia a partir do século VIII fez contribuições significativas para a matemática. Eles foram capazes de aproveitar e fundir os desenvolvimentos matemáticos tanto da Grécia como da Índia.

Uma consequência da proibição islâmica de representar a forma humana foi o uso extensivo de padrões geométricos complexos para decorar os seus edifícios, elevando a matemática à forma de uma arte. De fato, com o tempo, artistas muçulmanos descobriram todas as diferentes formas de simetria que podem ser retratadas em uma superfície bidimensional.

O próprio Qu’ran incentivou a acumulação de conhecimento, e uma Idade de Ouro da ciência e da matemática islâmica floresceu ao longo do período medieval dos séculos 9 a 15. A Casa da Sabedoria foi estabelecida em Bagdá por volta de 810, e o trabalho começou quase imediatamente na tradução das principais obras matemáticas e astronômicas gregas e indianas para o árabe.

O notável matemático persa Muhammad Al-Khwarizmi foi um dos primeiros diretores da Casa da Sabedoria no século IX, e um dos maiores dos primeiros matemáticos muçulmanos. Talvez a contribuição mais importante de Al-Khwarizmi para a matemática tenha sido sua forte defesa do sistema numérico hindu (1 – 9 e 0), que ele reconheceu como tendo o poder e a eficiência necessários para revolucionar a matemática islâmica (e, mais tarde, ocidental), e que foi logo adotada por todo o mundo islâmico, e mais tarde também pela Europa.

Al-Khwarizmi contribuiu com a álgebra e introduziu os métodos algébricos fundamentais de “redução” e “balanceamento” e forneceu um relato exaustivo da resolução de equações polinomiais até o segundo grau. Desta forma, ele ajudou a criar a poderosa linguagem matemática abstrata ainda hoje utilizada em todo o mundo e permitiu uma forma muito mais geral de analisar problemas que não apenas os problemas específicos anteriormente considerados pelos indianos e chineses.

>p>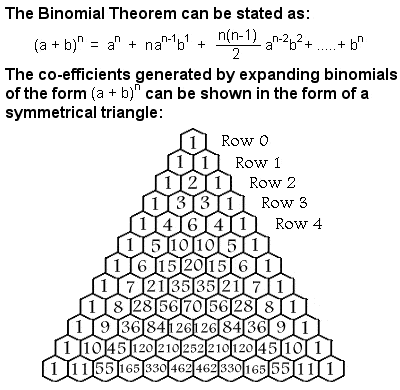br>>>p> Teorema Binomial>br>

O matemático persa Muhammad Al-Karaji do século X trabalhou para estender ainda mais a álgebra, liberando-a de sua herança geométrica, e introduziu a teoria do cálculo algébrico. Al-Karaji foi o primeiro a usar o método de prova por indução matemática para provar seus resultados, provando que a primeira afirmação numa sequência infinita de afirmações é verdadeira, e depois provando que, se qualquer afirmação na sequência é verdadeira, também o é a seguinte.

Teorema Binomial

Entre outras coisas, Al-Karaji usou a indução matemática para provar o teorema binomial. Um binômio é um tipo simples de expressão algébrica que tem apenas dois termos que são operados apenas por adição, subtração, multiplicação e expoentes positivos de números inteiros, tais como (x + y)2. Os co-eficientes necessários quando um binômio é expandido formam um triângulo simétrico, geralmente chamado de Triângulo de Pascal após o matemático francês Blaise Pascal do século XVII, embora muitos outros matemáticos o tivessem estudado séculos antes dele na Índia, Pérsia, China e Itália, incluindo Al-Karaji.

P>Alguns cem anos depois de Al-Karaji, Omar Khayyam (talvez mais conhecido como poeta e escritor do “Rubaiyat”, mas um importante matemático e astrônomo por direito próprio) generalizou métodos indianos de extração de raízes quadradas e em cubos para incluir a quarta, quinta e mais altas raízes no início do século 12. Ele realizou uma análise sistemática dos problemas cúbicos, revelando que na verdade existiam vários tipos diferentes de equações cúbicas. Embora ele tenha, de facto, conseguido resolver equações cúbicas, e embora lhe seja geralmente atribuída a identificação dos fundamentos da geometria algébrica, foi impedido de avançar devido à sua incapacidade de separar a álgebra da geometria, e um método puramente algébrico para a solução das equações cúbicas teve de esperar mais 500 anos e os matemáticos italianos del Ferro e Tartaglia tiveram de esperar mais 500 anos.

Trigonometria Esférica

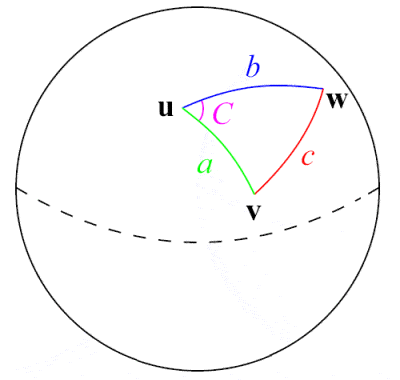
br>>>p>Al-Tusi foi um pioneiro no campo da trigonometria esférica

The 13th Century Persian astronomer, cientista e matemático Nasir Al-Din Al-Tusi foi talvez o primeiro a tratar a trigonometria como uma disciplina matemática separada, distinta da astronomia. Com base em trabalhos anteriores de matemáticos gregos como Menelaus de Alexandria e trabalhos indianos sobre a função seno, ele deu a primeira extensa exposição de trigonometria esférica, incluindo a lista dos seis casos distintos de um triângulo direito em trigonometria esférica. Uma de suas maiores contribuições matemáticas foi a formulação da famosa lei dos pecados para triângulos planos, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), embora a lei senoidal para triângulos esféricos tivesse sido descoberta anteriormente pelos persas Abul Wafa Buzjani e Abu Nasr Mansur, do século X.

Outros matemáticos muçulmanos medievais dignos de nota incluem:

• o Thabit árabe do século IX ibn Qurra, que desenvolveu uma fórmula geral pela qual números amigáveis poderiam ser derivados, redescobertos muito mais tarde por ambos Fermat e Descartes(números amigáveis são pares de números para os quais a soma dos divisores de um número é igual ao outro número, e.g. os divisores próprios de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, dos quais a soma é 284; e os divisores próprios de 284 são 1, 2, 4, 71 e 142, dos quais a soma é 220);

li>o matemático árabe do século 10 Abul Hasan al-Uqlidisi, que escreveu o texto sobrevivente mais antigo mostrando o uso posicional de números arábicos, e particularmente o uso de decimais em vez de frações (e.g. 7.375 insead de 73⁄8); o geômetro árabe do século 10 Ibrahim ibn Sinan, que continuou as investigações de Arquimedes sobre áreas e volumes, bem como sobre tangentes de um círculo;

• o século XI Ibn al-Haytham persa (também conhecido como Alhazen), que, além de seu trabalho pioneiro em ótica e física, estabeleceu o início da ligação entre álgebra e geometria, e idealizou o que agora é conhecido como “problema de Alhazen” (ele foi o primeiro matemático a derivar a fórmula para a soma das quatro potências, usando um método que é facilmente generalizável); e
• o século XIII Kamal al-Din al-Farisi persa, que aplicou a teoria das secções cónicas para resolver problemas ópticos, bem como prosseguiu o trabalho na teoria dos números, tais como em números amigáveis, factorização e métodos combinatórios;
• o Ibn al-Banna al-Marrakushi marroquino do século XIII, cujos trabalhos incluíram tópicos como o cálculo das raízes quadradas e a teoria das frações contínuas, bem como a descoberta do primeiro novo par de números amigáveis desde os tempos antigos (17.296 e 18.416, mais tarde redescobertos por Fermat) e o primeiro uso da notação algébrica desde Brahmagupta.

Com a influência sufocante do Império Otomano Turco a partir do século XIV ou XV, a matemática islâmica estagnou, e novos desenvolvimentos se deslocaram para a Europa.