Kom terug naar de Lessenindex | Doe de lessen op volgorde | Printvriendelijke pagina
De Factor Stelling
De Factor Stelling is een gevolg van de Resterende Stelling, en is gebaseerd op dezelfde redenering. Als je de les over de Reststelling nog niet hebt gelezen, bekijk dat onderwerp dan eerst, en kom dan hier terug.
Zoals de Reststelling aangeeft, als je een veelterm p(x) deelt door een factor x – a van die veelterm, dan krijg je een rest van nul. Laten we nog eens kijken naar die delingsalgoritme-uitdrukking van de veelterm:
Aanwijzing
p(x) = (x – a)q(x) + r(x)
Als x – a inderdaad een factor is van p(x), dan zal de rest na deling door x – a nul zijn. Dat wil zeggen:
p(x) = (x – a)q(x)
In termen van de Reststelling betekent dit dat, als x – a een factor is van p(x), de rest, als we synthetisch delen door
x = a, nul zal zijn.
Het punt van de Factortheorie is het omgekeerde van de Reststelling: Als je een polynoom synthetisch deelt door x = a en je krijgt een rest van nul, dan is niet alleen x = a een nulpunt van de polynoom (met dank aan de Remainder Theorem), maar x – a is ook een factor van de polynoom (met dank aan de Factor Theorem).
Net als bij de Remainder Theorem gaat het er hier niet om de lange deling van een gegeven polynoom door een gegeven factor uit te voeren. Deze stelling herhaalt niet wat je al weet, maar probeert je leven eenvoudiger te maken. Bij een oefening met de Stelling van de Factor zult u de synthetische deling toepassen en vervolgens controleren of de rest nul is.
- Gebruik de Factortheorie om te bepalen of x – 1 een factor is van
f (x) = 2×4 + 3×2 – 5x + 7.
Om te testen of x – 1 een factor is van f (x) = 2×4 + 3×2 – 5x + 7, zegt de Factortheorie dat x = 1 een nulpunt moet zijn van f (x). Om te testen of x – 1 een factor is, zal ik eerst x – 1 gelijk stellen aan nul en oplossen om het voorgestelde nulpunt, x = 1, te vinden. Dan zal ik synthetisch delen gebruiken om f (x) te delen door x = 1. Aangezien er geen kubieke term is, zal ik er goed aan denken een “0” in te voegen in de eerste regel van de synthetische deling om de weggelaten macht van x in 2×4 + 3×2 – 5x + 7 voor te stellen:
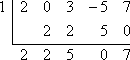
Omdat de rest niet nul is, zegt de Factortheorstelling dat:
x – 1 is geen factor van f (x).
- Gebruik makend van de Factortheorie, controleer of x + 4 een factor is van
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.
- Als x + 4 een factor is, dan is (door deze factor gelijk te stellen aan nul en op te lossen) x = -4 een wortel. Om de vereiste controle uit te voeren, moet ik nagaan dat, als ik synthetische deling toepas op f (x), met x = -4, ik een rest van nul krijg:
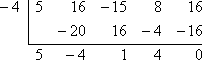
De rest is nul, dus de Factorstelling zegt dat:
- x + 4 is een factor van 5×4 + 16×3 – 15×2 + 8x + 16.
In de praktijk wordt de Factorstelling gebruikt bij het “volledig” ontbinden van veeltermen in factoren. In plaats van verschillende factoren te proberen met behulp van een lange deling, gebruik je synthetische deling en de Factor Stelling. Elke keer dat je deelt door een getal (zijnde een mogelijke wortel van de veelterm) en een nul rest krijgt in de synthetische deling, betekent dit dat het getal inderdaad een wortel is, en dus dat “x min het getal” een factor is. Vervolgens ga je verder met de deling met de resulterende kleinere veelterm, net zo lang tot je een lineaire factor hebt gevonden (dus alle factoren) of een kwadratische (waarop je de kwadratische formule kunt toepassen).
- Gebruikmakend van het feit dat -2 en 1/3 nulpunten zijn van f (x) = 3×4 + 5×3 + x2 + 5x – 2, factor je de veelterm volledig. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
Als x = -2 een nulpunt is, dan is x + 2 = 0, dus x + 2 is een factor. Evenzo, als x = 1/3 een nulpunt is, dan is x – 1/3 = 0, dus x – 1/3 is een factor. Door mij twee nullen te geven, hebben ze mij ook twee factoren gegeven: x + 2 en x – 1/3.
Omdat ik begonnen ben met een vierdegraads veelterm, houd ik een kwadriek over als ik deze twee gegeven factoren heb weggesplitst. Ik kan die kwadratische oplossen met de kwadratische formule of een andere methode.
De Factorstelling zegt dat ik de lange deling met de bekende factoren x + 2 en x – 1/3 niet hoef te doen. In plaats daarvan kan ik synthetische deling gebruiken met de bijbehorende nulpunten -2 en 1/3. Dit is wat ik krijg als ik de eerste deling doe met x = -2:
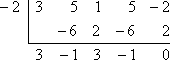
De rest is nul, wat te verwachten was omdat ze me in het begin hadden verteld dat -2 een bekend nulpunt van de polynoom was. In plaats van opnieuw te beginnen met het oorspronkelijke polynoom, ga ik nu aan de slag met de resterende polynoomfactor van 3×3 – x2 + 3x – 1 (van de onderste regel van de synthetische deling). Ik zal deze delen door het andere gegeven nulpunt, x = 1/3:
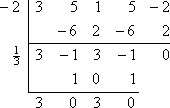
Dus blijft over de kwadratische 3×2 + 3, die ik kan oplossen:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Als de nulpunten x = -i en x = i zijn, dan zijn de factoren x – (-i) en x – (i), of x + i en x – i. I need to remember that I divided off a “3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. “The Factor Theorem.” Purplemath. Available from 2016
|