Voordelen van het gebruik van instrumentele variabelen om causaliteit aan te tonen
Als voorbeeld nemen we de kwestie van het schatten van het effect van onderwijs op inkomens. De eenvoudigste schattingstechniek, ordinary least squares (OLS), levert schattingen op waaruit blijkt dat een extra jaar opleiding gepaard gaat met 6-10% hogere verdiensten. De positieve relatie kan echter het gevolg zijn van zelfselectie in het onderwijs; d.w.z. dat personen die het meest te winnen hebben bij meer onderwijs, eerder geneigd zullen zijn te blijven. Dit zal bijvoorbeeld het geval zijn wanneer leerlingen met hogere capaciteiten studeren gemakkelijker vinden en waarschijnlijk toch een hoger loon zouden ontvangen. De positieve correlatie die tussen het aantal onderwijsjaren en de lonen wordt waargenomen, zou dus gedeeltelijk de premie voor bekwaamheid weerspiegelen en zou niet kunnen worden geïnterpreteerd als het rendement van een extra jaar onderwijs, zoals de bedoeling is. OLS-schattingen zouden dus niet informatief zijn over het effect van een beleid dat erop gericht is het aantal jaren onderwijs te verhogen. Dit probleem wordt “omitted variable bias” genoemd. Het doet zich voor wanneer een variabele (zoals bekwaamheid) die niet door de onderzoeker wordt waargenomen, gecorreleerd is met zowel de behandeling (meer opleiding) als met het resultaat (inkomen). De richting (over- of onderschatting) en de grootte van de vertekening in OLS schattingen is een functie van het teken en de sterkte van de correlaties.
In dit voorbeeld is een randomized control trial (RCT), waarbij onderwijs willekeurig aan individuen zou worden toegewezen en de verschillen in hun lonen gedurende hun leven zouden worden geobserveerd, om ethische redenen eenvoudigweg niet haalbaar. Sommige natuurlijke of quasi-natuurlijke experimenten kunnen echter in de buurt komen van een wijziging van de onderwijskeuze voor bepaalde groepen individuen, en kunnen als zodanig als instrumenten worden gebruikt. Een dergelijk natuurlijk experiment is een wijziging van de wettelijke minimumleeftijd waarop leerlingen de school mogen verlaten (schoolverlatersleeftijd). Dit soort verandering treft alle leerlingen, ongeacht hun capaciteiten. Zij werkt dus als een externe schok die niet door de individuele leerling kan worden beïnvloed.
In tal van landen is bij wet bepaald op welke leeftijd leerlingen het onderwijssysteem mogen verlaten. Stel bijvoorbeeld dat een kind de school op de laatste dag van het schooljaar mag verlaten als het eind augustus 14 jaar is. Stel nu dat de wetgeving wordt gewijzigd, zodat kinderen eind augustus 15 jaar moeten zijn om de school te mogen verlaten. Kinderen die de school op hun 14e wilden verlaten, mogen dat niet en moeten nog een jaar extra naar school. Onder de (sterke) aanname dat kinderen onder de twee wetgevingen vergelijkbaar zijn en met vergelijkbare arbeidsmarktomstandigheden te maken hebben, creëert de wetswijziging een quasi-natuurlijk experiment: onafhankelijk van hun capaciteiten zullen sommige individuen de gevolgen ondervinden van de wijziging in de leerplichtige leeftijd en een extra jaar moeten blijven, terwijl leerlingen met vergelijkbare voorkeuren uit het vorige cohort dat niet zullen doen. Indien de onderzoekers wisten wie de school op 14 jaar wilde verlaten, konden zij de resultaten van de individuen die de school op 14 jaar verlieten vergelijken met de resultaten van de individuen die gedwongen werden tot 15 jaar te blijven. Dit eenvoudige verschil zou dan het causale effect zijn van het op school blijven tussen de leeftijd van 14 en 15 jaar. Helaas maken de observatiegegevens het niet mogelijk de personen te identificeren wier onderwijskeuze door de hervorming werd beïnvloed; onder de nieuwe wetgeving kunnen personen die de school op 15 jaar wilden verlaten dus niet worden onderscheiden van degenen die op 14 jaar de school wilden verlaten maar nog een jaar moesten blijven. De hervorming verandert echter wel de kans dat men op school blijft, en kan dus als instrument worden gebruikt, aangezien zij van invloed is op de kans op een behandeling (nog een jaar school) zonder dat de uitkomst van belang (bv. inkomsten) wordt beïnvloed.
In 1947 werd door een wetswijziging in het Verenigd Koninkrijk de minimumleeftijd voor het verlaten van de school verhoogd van 14 tot 15 jaar, wat gevolgen had voor kinderen die in 1933 en daarna waren geboren. Deze wetswijziging biedt de mogelijkheid om het effect van (extra) scholing op het inkomen te evalueren. In figuur 1 laat paneel A zien dat de hervorming van invloed was op zowel de fractie van kinderen die de school bij de eerste gelegenheid verlieten (linkergrafiek) als op de totale hoeveelheid voltooide schoolopleiding (rechtergrafiek). Uit de schattingen blijkt dat de hervorming het gemiddelde aantal jaren schoolopleiding voor mannen met 0,397 jaar heeft doen toenemen. Deze schatting van het effect van de hervorming (de IV) op de behandeling (onderwijs) staat bekend als de “regressie in de eerste fase”. Indien onderwijs een causaal effect heeft op de lonen, zouden wij moeten vaststellen dat de gemiddelde lonen van de personen die door de hervorming worden getroffen ook hoger zijn. Dit is inderdaad het geval, zoals blijkt uit deel B van figuur 1, waarin het gemiddelde logarishuisloon voor mannen wordt vermeld. Deze reeks vertoont een duidelijke breuk in 1933, waarvan de grootte impliceert dat personen die door de hervorming worden getroffen, gemiddeld 1,2% meer verdienen. Deze tweede schatting van het effect van de hervorming (de IV) op de uitkomst (de lonen) staat bekend als de “gereduceerde vormschatting”. Een eenvoudige IV-strategie, in dit geval met gebruikmaking van een binair instrument dat slechts twee waarden aanneemt (1 voor de invloed van de hervorming en 0 voor de afwezigheid van de invloed van de hervorming), is de verhouding van de schatting in de gereduceerde vorm tot de schatting in de eerste fase. (Deze verhouding staat ook bekend als de Wald-raming.) In dit geval zou het causale effect van extra onderwijs op de inkomens 0,012/0,397 = 0,030 en dus ongeveer 3% bedragen.
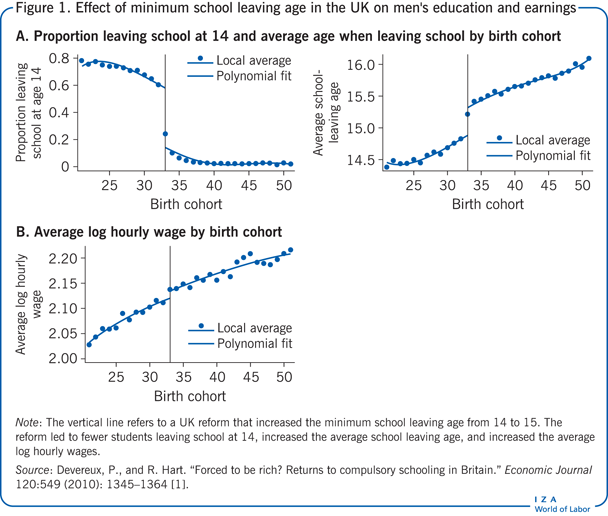
De intuïtie van deze benadering is dat het effect van één jaar extra onderwijs op de lonen in feite het effect van de hervorming (het IV) op de lonen (het resultaat) is – dat in de verkorte vorm wordt gegeven -, verhoogd met het effect van de hervorming op het aantal onderwijsjaren (de behandeling) – dat is waar de schatting in de eerste fase over gaat. Indien het instrument “relevant” is, d.w.z. een effect heeft op het onderwijs (de behandeling), en indien het instrument de lonen “uitsluitend” beïnvloedt via zijn effect op het onderwijs, dan kunnen de IV-schattingen worden geïnterpreteerd als het causale effect van de behandeling op het resultaat. Deze twee voorwaarden worden “instrumentrelevantie” en “uitsluitingsbeperking” genoemd.
Samengevat: als een niet-waargenomen variabele zoals bekwaamheid zowel met de behandeling als met de uitkomst correleert, zal een eenvoudige schatting zoals OLS een vertekend beeld geven als gevolg van zelfselectie in de behandeling. Evenzo zal, als de behandelingsvariabele foutief wordt gemeten, de OLS-schatting vertekend zijn in de richting van nul. Een causale schatting van een behandeling op een uitkomst kan echter worden verkregen als een geloofwaardig instrument kan worden gevonden. Een geloofwaardig instrument moet aan twee voorwaarden voldoen:
-
Relevantie: het instrument moet van invloed zijn op de waarschijnlijkheid van de behandeling. In een regressie van de behandeling op het instrument, ook wel de eerste-fasevergelijking genoemd, moet de coëfficiënt op de IV voldoende sterk zijn.
-
Uitsluitingsrestrictie: het instrument beïnvloedt de uitkomst uitsluitend via zijn effect op de behandeling.
Als een dergelijke IV kan worden gevonden (d.w.z.
In het vorige voorbeeld werd de Wald-schatting gepresenteerd, d.w.z. de verhouding van de schattingen uit twee regressies: de schatting in de gereduceerde vorm, afkomstig uit een regressie van de uitkomst op het instrument; en de schatting in de eerste fase, afkomstig uit een regressie van de behandeling op het instrument. Dit kan gemakkelijk worden berekend wanneer het instrument slechts twee waarden heeft. In het meer algemene geval wordt een zogenaamde “tweetraps kleinste kwadraten”-schatting (2SLS) berekend, waarbij de voorspellingen van de behandeling uit de vergelijking van de eerste fase worden gebruikt in een regressie van de uitkomst op de behandeling, in plaats van de werkelijke waarde van de behandeling. Aldus wordt alleen de uit het instrument afkomstige variatie in de behandeling gebruikt om de variantie in de uitkomst te verklaren. Dit lost dan de zelfselectievertekening op. In het geval van een binair (twee-waarden) instrument zullen de Wald- en 2SLS-schattingen identiek zijn (zie bijvoorbeeld). De moeilijkheid zit echter niet in de implementatie van zo’n 2SLS-schatting, alle statistische pakketten kunnen IV-schattingen berekenen, maar in (a) het vinden van een geldig instrument en (b) het interpreteren van de resultaten. De discussie zal zich nu op deze twee punten toespitsen.