ISLAMISCHE WETENSCHAP

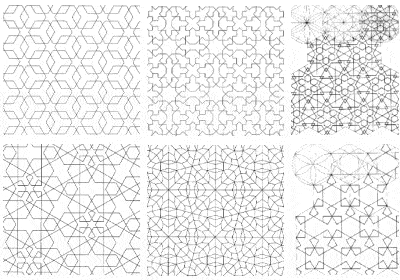
Een paar voorbeelden van de complexe symmetrieën die in de islamitische tempelversiering werden gebruikt

Het islamitische rijk dat vanaf de 8e eeuw in Perzië, het Midden-Oosten, Centraal-Azië, Noord-Afrika, Iberia en delen van India werd gesticht, leverde een belangrijke bijdrage aan de wiskunde. Zij waren in staat om te putten uit de wiskundige ontwikkelingen van zowel Griekenland als India en deze samen te smelten.

Een gevolg van het islamitische verbod op het afbeelden van de menselijke vorm was het uitgebreide gebruik van complexe geometrische patronen om hun gebouwen te versieren, waardoor de wiskunde tot kunst werd verheven. In feite ontdekten Moslim kunstenaars in de loop van de tijd alle verschillende vormen van symmetrie die op een 2-dimensionaal oppervlak kunnen worden afgebeeld.

De Koran zelf moedigde het vergaren van kennis aan, en een Gouden Eeuw van Islamitische wetenschap en wiskunde bloeide gedurende de middeleeuwse periode van de 9e tot de 15e Eeuw. Het Huis van Wijsheid werd rond 810 in Bagdad opgericht, en er werd vrijwel onmiddellijk begonnen met het vertalen van de belangrijkste Griekse en Indiase wiskundige en astronomische werken in het Arabisch.

De uitmuntende Perzische wiskundige Muhammad Al-Khwarizmi was een vroege directeur van het Huis van Wijsheid in de 9e Eeuw, en een van de grootste van de vroege Moslim wiskundigen. Misschien wel Al-Khwarizmi’s belangrijkste bijdrage aan de wiskunde was zijn sterke pleidooi voor het Hindoe numerieke systeem (1 – 9 en 0), waarvan hij erkende dat het de kracht en efficiëntie had die nodig was om een revolutie teweeg te brengen in de Islamitische (en later ook de Westerse) wiskunde, en dat al snel door de hele Islamitische wereld, en later ook door Europa, werd overgenomen.

Al-Khwarizmi’s andere belangrijke bijdrage was algebra, en hij introduceerde de fundamentele algebraïsche methoden van “reductie” en “balanceren” en gaf een uitputtende beschrijving van het oplossen van polynomiale vergelijkingen tot de tweede graad. Op deze manier hielp hij bij het creëren van de krachtige abstracte wiskundige taal die vandaag de dag nog steeds over de hele wereld wordt gebruikt, en maakte hij een veel algemenere manier mogelijk om problemen te analyseren dan alleen de specifieke problemen die voorheen door de Indiërs en Chinezen werden overwogen.

Binomiale Stelling

De 10e-eeuwse Perzische wiskundige Muhammad Al-Karaji werkte aan een nog verdere uitbreiding van de algebra, door deze te bevrijden van zijn meetkundige erfenis, en introduceerde de theorie van de algebraïsche calculus. Al-Karaji was de eerste die de methode van bewijs door wiskundige inductie gebruikte om zijn resultaten te bewijzen, door te bewijzen dat de eerste uitspraak in een oneindige reeks van uitspraken waar is, en vervolgens te bewijzen dat, als een uitspraak in de reeks waar is, de volgende dat ook is.

Binomiale stelling

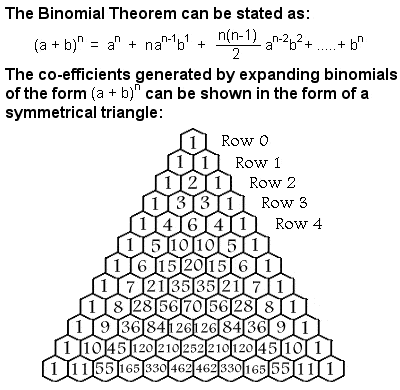
Al-Karaji gebruikte onder andere wiskundige inductie om de binomiale stelling te bewijzen. Een binomiaal is een eenvoudige algebraïsche uitdrukking met slechts twee termen, die alleen door optellen, aftrekken, vermenigvuldigen en positieve exponenten in gehele getallen, zoals (x + y)2, kunnen worden bewerkt. De coëfficiënten die nodig zijn wanneer een binomiaal wordt geëxpandeerd vormen een symmetrische driehoek, gewoonlijk de Driehoek van Pascal genoemd naar de 17e eeuwse Franse wiskundige Blaise Pascal, hoewel vele andere wiskundigen deze al eeuwen voor hem in India, Perzië, China en Italië hadden bestudeerd, waaronder Al-Karaji.

Honderd jaar na Al-Karaji, veralgemeende Omar Khayyam (misschien beter bekend als dichter en schrijver van de “Rubaiyat”, maar een belangrijk wiskundige en astronoom in zijn eigen recht) de Indiase methoden voor de extractie van vierkants- en kubuswortels naar vierde, vijfde en hogere wortels in het begin van de 12e eeuw. Hij voerde een systematische analyse uit van kubische problemen, waaruit bleek dat er in feite verschillende soorten kubische vergelijkingen bestonden. Hoewel hij er in feite in slaagde kubische vergelijkingen op te lossen, en hoewel hem gewoonlijk wordt toegeschreven dat hij de grondslagen van de algebraïsche meetkunde heeft gelegd, werd hij van verdere vooruitgang weerhouden door zijn onvermogen de algebra van de meetkunde te scheiden, en een zuiver algebraïsche methode voor de oplossing van kubische vergelijkingen moest nog eens 500 jaar wachten op de Italiaanse wiskundigen del Ferro en Tartaglia.

Sferische trigonometrie

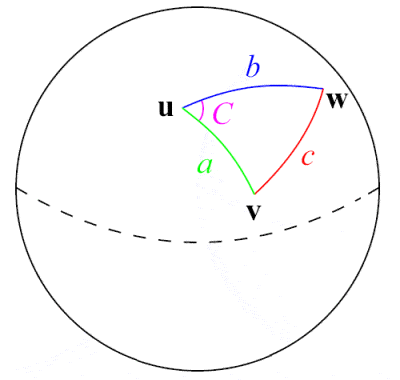
Al-Tusi was een pionier op het gebied van sferische trigonometrie

De 13e-eeuwse Perzische astronoom, wetenschapper en wiskundige Nasir Al-Din Al-Tusi was misschien wel de eerste die trigonometrie als een aparte wiskundige discipline behandelde, los van astronomie. Voortbouwend op eerder werk van Griekse wiskundigen zoals Menelaus van Alexandrië en Indiaas werk aan de sinusfunctie, gaf hij de eerste uitgebreide uiteenzetting van sferische trigonometrie, inclusief een opsomming van de zes verschillende gevallen van een rechthoekige driehoek in sferische trigonometrie. Een van zijn belangrijkste wiskundige bijdragen was de formulering van de beroemde sinuswet voor vlakke driehoeken, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), hoewel de sinuswet voor sferische driehoeken al eerder was ontdekt door de Perzen Abul Wafa Buzjani en Abu Nasr Mansur uit de 10e eeuw.

Andere vermeldenswaardige middeleeuwse moslim-wiskundigen zijn:

• de 9e-eeuwse Arabier Thabit ibn Qurra, die een algemene formule ontwikkelde waarmee amicale getallen konden worden afgeleid, veel later herontdekt door zowel Fermat als Descartes (amicale getallen zijn paren getallen waarvan de som van de delers van het ene getal gelijk is aan het andere getal, bijv.b.v. de eigen delers van 220 zijn 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 en 110, waarvan de som 284 is; en de eigen delers van 284 zijn 1, 2, 4, 71, en 142, waarvan de som 220 is);
• de 10e eeuwse Arabische wiskundige Abul Hasan al-Uqlidisi, die de vroegste bewaard gebleven tekst schreef waarin het positionele gebruik van Arabische cijfers wordt getoond, en in het bijzonder het gebruik van decimalen in plaats van breuken (b.v. 7.g. 7.375 in plaats van 73⁄8);
• de 10e eeuwse Arabische geometer Ibrahim ibn Sinan, die Archimedes’ onderzoek naar oppervlakten en volumes voortzette, alsmede naar de raaklijnen van een cirkel;
• de 11e-eeuwse Perziër Ibn al-Haytham (ook bekend als Alhazen), die niet alleen baanbrekend werk verrichtte op het gebied van optica en natuurkunde, maar ook een begin maakte met het verband tussen algebra en meetkunde, en het probleem bedacht dat nu bekend staat als “Alhazen’s probleem” (hij was de eerste wiskundige die de formule voor de som van de vierde machten afleidde, volgens een methode die gemakkelijk te veralgemenen is); en
• de 13e-eeuwse Perziër Kamal al-Din al-Farisi, die de theorie van de kegelsneden toepaste om optische problemen op te lossen, en ook werk verrichtte in de getaltheorie, zoals op het gebied van amicale getallen, factorisatie en combinatorische methoden;
• de Marokkaan Ibn al-Banna al-Marrakushi uit de 13e eeuw, die onderwerpen als het berekenen van vierkantswortels en de theorie van de doorlopende breuken, alsmede de ontdekking van het eerste nieuwe paar amicale getallen sinds de oudheid (17.296 en 18.416, later herontdekt door Fermat) en het eerste gebruik van algebraïsche notatie sinds Brahmagupta, in zijn werk heeft opgenomen.

Met de verstikkende invloed van het Turkse Ottomaanse Rijk vanaf de 14e of 15e eeuw stagneerde de islamitische wiskunde, en verplaatsten verdere ontwikkelingen zich naar Europa.

<< Terug naar Madhava

Voorwaarts naar Al-Khwarizmi >>