O Teorema do Fator

p>Volta ao Índice de Lições | Faça as Lições por Ordem | Página Amigável para Impressão
p> O Teorema do Fator

O Teorema do Fator é um resultado do Teorema do Restante, e é baseado no mesmo raciocínio. Se você não leu a lição sobre o Teorema do Restante, reveja esse tópico primeiro, e depois retorne aqui.

Como o Teorema do Restante aponta, se você dividir um polinômio p(x) por um fator x – a desse polinômio, então você terá um saldo zero. Vamos olhar novamente para essa expressão de Algoritmo de Divisão do polinômio:

p(x) = (x – a)q(x) + r(x)

se x – a é de fato um fator de p(x), então o restante após a divisão por x – a será zero. Isto é:

p(x) = (x – a)q(x)

Em termos do Teorema do Restante, isto significa que, se x – a é um fator de p(x), então o restante, quando fazemos divisão sintética por
x = a, será zero.

O ponto do Teorema do Fator é o inverso do Teorema do Restante: Se você dividir um polinômio sintético por x = a e obter um restante de zero, então, não só x = um zero do polinômio (cortesia do Teorema do Restante), mas x – a é também um fator do polinômio (cortesia do Teorema do Fator).

Apenas como com o Teorema do Restante, o ponto aqui não é fazer a divisão longa de um determinado polinômio por um determinado fator. Este Teorema não está repetindo o que você já sabe, mas está tentando tornar sua vida mais simples. Quando confrontado com um exercício do Teorema do Fator, você aplicará a divisão sintética e então verificará se há um remanescente zero.

• Utiliza o Teorema dos Factores para determinar se x – 1 é um factor de
  f (x) = 2×4 + 3×2 – 5x + 7.

Para x – 1 ser um factor de f (x) = 2×4 + 3×2 – 5x + 7, o Teorema dos Factores diz que x = 1 deve ser um zero de f (x). Para testar se x – 1 é um fator, primeiro vou definir x – 1 igual a zero e resolver para encontrar o zero proposto, x = 1. Depois vou usar a divisão sintética para dividir f (x) por x = 1. Como não há um termo em cubo, terei o cuidado de lembrar de inserir um “0” na primeira linha da divisão sintética para representar a potência omitida de x em 2×4 + 3×2 – 5x + 7:

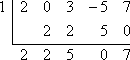
p>P>Posto que o restante não é zero, então o Teorema do Fator diz que:

x – 1 não é um fator de f (x).

• Usando o Teorema do Fator, verifique que x + 4 é um fator de
  f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.

Se x + 4 é um fator, então (definindo este fator igual a zero e resolvendo) x = -4 é uma raiz. Para fazer a verificação necessária, preciso verificar que, quando uso divisão sintética em f (x), com x = -4, obtenho um remanescente zero:

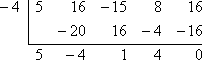
O restante é zero, então o Teorema do Fator diz que:

x + 4 é um fator de 5×4 + 16×3 – 15×2 + 8x + 16.

Na prática, o Teorema do Factor é utilizado quando se factoram os polinómios “completamente”. Ao invés de tentar vários fatores usando divisão longa, você usará divisão sintética e o Teorema do Fator. Sempre que você dividir por um número (sendo uma raiz potencial do polinômio) e obter um zero restante na divisão sintética, isto significa que o número é realmente uma raiz, e assim “x menos o número” é um fator. Então você continuará a divisão com o polinômio menor resultante, continuando até chegar a um fator linear (assim você encontrou todos os fatores) ou um quadrático (ao qual você pode aplicar a Fórmula Quadrática).

• Usando o fato de que -2 e 1/3 são zeros de f (x) = 3×4 + 5×3 + x2 + 5x – 2, fator o polinômio completamente. Copyright © Elizabeth Stapel 2002-2011 Todos os direitos reservados

Se x = -2 é um zero, então x + 2 = 0, então x + 2 é um fator. Da mesma forma, se x = 1/3 é um zero, então x – 1/3 = 0, então x – 1/3 é um fator. Ao me dar dois dos zeros, eles também me deram dois fatores: x + 2 e x – 1/3.

Desde que comecei com um polinómio de quarto grau, então ficarei com um quadrático assim que dividir estes dois factores. Posso resolver esse quadrático usando a Fórmula Quadrática ou algum outro método.

O Teorema do Fator diz que eu não tenho que fazer a divisão longa com os fatores conhecidos de x + 2 e x – 1/3. Em vez disso, posso usar a divisão sintética com os zeros -2 e 1/3 associados. Aqui está o que recebo quando faço a primeira divisão com x = -2:

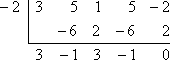
O resto é zero, o que é esperado porque me disseram no início que -2 era um zero conhecido do polinómio. Em vez de começar de novo com o polinômio original, vou agora trabalhar no fator polinomial restante de 3×3 – x2 + 3x – 1 (a partir da linha de fundo da divisão sintética). Vou dividir isto pelo outro zero dado, x = 1/3:

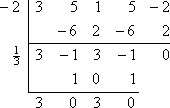
Isto deixa-me com o quadrático 3×2 + 3, que eu posso resolver:

3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i

Se os zeros são x = -i e x = i, então os fatores são x – (-i) e x – (i), ou x + i e x – i. I need to remember that I divided off a “3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:

3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)

Top | Return to Index