Istnieją drzewa genealogiczne i populacje, w których zasada kojarzenia panmiktycznego jest zasadniczo złamana. Zazwyczaj jest to geograficznie lub społecznie stosunkowo izolowane małe społeczności. W takich społecznościach inbreeding, czyli kojarzenie krewniacze różnych rzędów (rodzic – dziecko, rodzeństwo, kuzyni, wujek – siostrzenica, itd.
Problem wpływu chowu wsobnego na populację jest ważnym problemem genetyki 1. Obecnie problem ten nie doczekał się jeszcze ostatecznego rozwiązania.
W większości przypadków inbredu w drzewie genealogicznym bierze się pod uwagę trzy pokolenia. To najodleglejsi krewni, którzy są brani pod uwagę przy kojarzeniu krewniaczym, są drugimi kuzynami.
Krewniactwo uwzględnia się za pomocą współczynnika inbredu.
Współczynnik inbredu jest to prawdopodobieństwo, że dwa allele są identyczne ze względu na pochodzenie.
Rozważmy metodę obliczania współczynnika inbredu w drzewie genealogicznym zaproponowaną przez Wrighta 1, 2.
Do znalezienia współczynnika inbredu konieczne jest:
znaleźć dla potomków zawierających małżeństwo wszystkie drogi w drzewie genealogicznym, które poprzez wspólnego przodka łączą tych potomków.
Odliczyć liczbę kroków (przemian pokoleń) na każdej drodze.
Wtedy współczynnik inbredu jest równy:
 ……(1)
……(1)
gdzie r jest liczbą dróg, m1, m2, …. mi- liczba kroków na każdej drodze.
Po raz kolejny zauważymy, że liczba addytywów w sumie (1) jest równa liczbie dróg, które przez wspólnych przodków łączą małżeństwa.
Rozważmy konkretne przypadki drzew genealogicznych, rysunek 1. Na tym rysunku kwadrat oznacza osobnika płci męskiej, a koło – osobnika płci żeńskiej. Linie przerywane i identyczne cyfry określają możliwe drogi w drzewie genealogicznym, które poprzez wspólnego przodka (mężczyznę lub kobietę) łączą potomków w małżeństwo. Na niektórych miejscach dróg, rysunek 1с, znajdują się dwie cyfry 1 i 2. To określa, że takie miejsca są wspólne dla różnych sposobów.
Małżeństwo ojciec – córka jest kazirodztwo, rysunek 1а. Potomek (kobieta) jest połączony z przodkiem (mężczyzną) tam 1 drogą z jednym krokiem, czyli m = 1. Stąd występuje współczynnik inbredu.
Ft = 1/2,2-1 = 1/4
Istnieje małżeństwo brat – siostra (sibs), rysunek 1b. Cyfry określają numer drogi. Liczba identycznych cyfr na drodze od żeniącego się mężczyzny do kobiety jest równa liczbie kroków.
Niech każdy potomek, który się ożenił łączy się z partnerką dwiema drogami po dwa kroki na każdej drodze, czyli m = 2. Stąd występuje współczynnik inbredu.
Ft = 1/2.(2-2 + 2-2) = 1/4
Małżeństwo między kuzynami pokazane jest na rysunku 1с.
Rysunek 1. Niektóre rodzaje chowu wsobnego w drzewie genealogicznym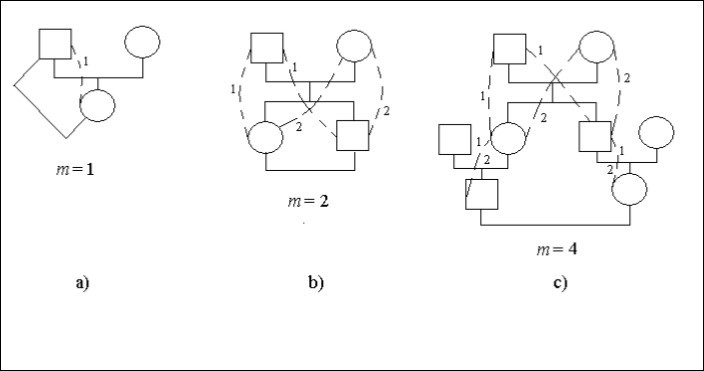
Każdy potomek, który się ożenił, łączy się z partnerem na 2 sposoby po 4 kroki na każdym z nich, czyli m = 4. Stąd istnieje współczynnik inbredu.
Ft = 1/2.(2-4 + 2-4) = 1/16
Wzór (1) jest łatwy do zrozumienia z następującej logiki.
Oczywiście tam 1/2 genów dziecka jest wspólnych z każdym z rodziców, 1/4 – z dziadkiem i babcią, 1/8 – z pradziadkiem i prababcią itd. Jeśli od kobiety do dowolnego przodka prowadzi droga z η kroków, to udział wspólnych genów z tym przodkiem jest równy 2-η. Jeśli od mężczyzny do dowolnego przodka prowadzi droga o μ kroków, to udział wspólnych genów jest równy 2-μ. W momencie ślubu mężczyzny i kobiety ze wspólnym przodkiem udział wspólnych genów z tym przodkiem będzie równy 2-η. 2-μ = 2-m gdzie m = η + μ jest całkowitą liczbą kroków przez wspólnego przodka od kobiety aż do ślubu mężczyzny. Wielkość 1/2 2-m pokazuje prawdopodobieństwo, że gen przypadkowo wybrany u kobiety będzie identyczny pod względem pochodzenia z genem przypadkowo wybranym u mężczyzny. Ta sama wielkość podaje wkład do współczynnika inbredu Ft w jedną stronę przez wspólnego przodka od kobiety do mężczyzny wychodzącego za mąż.
Na przykład, jeśli wspólny przodek będzie oddalony od małżeństwa o η = μ = 5 pokoleń to prawdopodobieństwo, że będą mieli wspólny gen jest równe. 1/2 2-(5+5) = 1/2048 Wielkość ta przy analizie kojarzenia może być pominięta. (Tabela 1)
Tabela 1.Współczynniki inbredu dla niektórych małżeństw konsanguineous są pokazane dodatkowo.
| Rodzaj małżeństwa pokrewieństwa | Współczynnik pokrewieństwa Ft | |
| Drugie kuzynostwo | 1/32 | |
| Kuzynostwo wujek – siostrzenica | 1/32 | |
| Kuzynostwo niece | 1/32 | |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: pochodzenie identycznych alleli w homologicznych autosomach jest niekonsangwiniczne (prawdopodobieństwo tej hipotezy wynosi P(H1) = 1- Ft )i powstaje homozygotaа (warunkowe prawdopodobieństwo tego zdarzenia wynosi P(aa/H1) = q2) lub pochodzenie identycznych alleli jest konsangwiniczne (prawdopodobieństwo tej hipotezy wynosi P(H2) = Ft ) i powstaje homozygotaа (warunkowe prawdopodobieństwo tego zdarzenia wynosi P(aa/H2) = q). Prawdopodobieństwo q wystąpienia homozygoty aa w tym drugim przypadku jest określone przez to, że jeśli allel a jest w jednym autosomie, to przy pokrewieństwie homozygoty ten sam allel koniecznie powinien być i w autosomie homologicznym.
Więc całkowite prawdopodobieństwo wystąpienia homozygoty recesywnej jest równe:
 ……….(3)
……….(3)
Gdy weźmiemy pod uwagę p = 1 – q istnieje częstość allelu dominującego a.
Podobnie znajduje się tam całkowite prawdopodobieństwo wystąpienia dominującej homozygoty AA przy losowym kojarzeniu:
 ……….. (4)
……….. (4)
Tak więc, zgodnie z (3) i (4) całkowita częstość homozygot (dominujących i recesywnych) w drzewie genealogicznym inbredów wzrasta na 2Ftpq. Stąd częstość heterozygot maleje dla tej samej wielkości i staje się równa 2pq – 2pqFt = 2pq(1-Ft), ponieważ suma częstości wszystkich zygot jest równa 1.
Wobec współczynnika inbredu, a także (3) i (4) prawa Hardy’ego – Weinberga w kolejnym pokoleniu drzewa genealogicznego dla genomu autosomalnego należy zapisać rozkłady genotypów zygoty jako 4:
 …………(5)
…………(5)
Gdzie pn oznacza częstość alleli dominujących A w pokoleniu n, qn – częstość alleli recesywnych a, zatem pn + qn = 1.
Współczynnik (5) odnosi się również do współczynnika Wrighta 5. Współczynnik Wrighta pokazuje, że w drzewie genealogicznym po kojarzeniu krewniaczym osobników obserwuje się następujące efekty: następuje wzrost frakcji homozygot autosomalnych w drzewie genealogicznym na Ft pnqn i spadek frakcji heterozygot autosomalnych w (1-F1) jedynkach w porównaniu z populacją panmikryczną.
Ale już przez jedno pokolenie przywracana jest równowaga Hardy’ego-Weinberga, która określa małe znaczenie osobnego kojarzenia konsanginicznego dla drzewa genealogicznego:
 ………(6)
………(6)
Oczywiście, dla całej populacji osobny akt kojarzenia konsanginicznego będzie miał jeszcze mniejsze znaczenie niż dla drzewa genealogicznego.
Ten sam efekt zmienności częstości genotypów zygoty jest obserwowany i dla genów sprzężonych z płcią.
Dystrybucję genotypów sprzężonych z chromosomem Х w panmiktycznym drzewie genealogicznym opisuje prawo Hardy’ego – Weinberga jako 1:
 ………..(7)
………..(7)
Częstość alleli dominujących A oznaczymy u mężczyzn pm, a u kobiet pf. Dla alleli recesywnycha jest to odpowiednio qm i qf .
Przy kojarzeniu istnieje stosunek genotypów u kobiet zgodny z iloczynem (pf + qf) (pm +qm).
Znajdźmy całkowite prawdopodobieństwo wystąpienia homozygoty recesywnej aa przy kojarzeniu losowym dla genów córki związanych z chromosomem X na podstawie wzoru (2). Logika zdarzeń jest podobna jak w przypadku autosomów, z tą różnicą, że warunkowe prawdopodobieństwo wystąpienia genotypuаа z alleli niekompangenicznych zgodnie z (7) jest równe P(aa/H1) = qmnqfn. Dla alleli konsanginicznych warunkowe prawdopodobieństwo wystąpienia genotypuаa jest równe P(aa/H2) = qf(n+1). U córek, tj. w pokoleniu n+1 prawdopodobieństwo wystąpienia homozygoty aa jest określone tym, że jeżeli allel a znajduje się w jednym chromosomie Х, to przy awangardowym pochodzeniu homozygoty ten sam allel koniecznie powinien być i w homologicznym chromosomie Х.
Więc całkowite prawdopodobieństwo wystąpienia homozygoty recesywnej jest równe:
 ……(8)
……(8)
gdzie pmn jest częstością występowania alleli dominujących A w pokoleniu n u mężczyzn, a pfn – u kobiet. Dla alleli recesywnych a odpowiednio qmn i qfn . Poza tym stosuje się qmn =1 – qmn i pfn = 1 – qfn.
Podobnie znajdując całkowite prawdopodobieństwo wystąpienia homozygoty dominującej stosujemy:
 ,
,
 ……….(9)
……….(9)
i heterozygoty P(Aa) = 1- P(aa) – P(AA) znajdziemy rozkład genotypów w Х-chromosomach drzewa rodowego wsobnego przy kojarzeniu:
 ……..(10)
……..(10)
Wykazano jednocześnie, że tak samo jak w autosomach, dodatki inbredowe w częstościach homozygoty dominującej i recesywnej w chromosomach sprzężonych z płcią są identyczne.
Inny sposób znalezienia proporcji (10) będzie polegał na tym, że
Znajdźmy najpierw całkowite prawdopodobieństwo wystąpienia heterozygoty Aa, czyli P(Aa) przy okazji losowego kojarzenia krewniaczego. Prawdopodobieństwo to wynika z następującej logiki kojarzenia: pochodzenie alleli jest niekonsangwiniczne (prawdopodobieństwo tej hipotezy wynosi P(H1) = 1 – Ft ) powstaje również heterozygota Aа (warunkowe prawdopodobieństwo tego zdarzenia wynosi P(Aa/H1) = pmnqfn + pfnqmn, patrz wzór (7)) lub pochodzenie alleli jest pokrewieństwa (prawdopodobieństwo tej hipotezy wynosi P(H2) = Ft) i powstaje heterozygota Aа (warunkowe prawdopodobieństwo tego zdarzenia jest równe zeru P(Aa/H2) = 0 ). Ostatnie stwierdzenie jest określone przez to, że przy pokrewieństwie podobnych alleli w homologicznych chromosomach nie może powstać heterozygota Aa składająca się z różnych alleli.
Więc korzystając ze wzoru na prawdopodobieństwo całkowite znajdujemy prawdopodobieństwo całkowite wystąpienia heterozygoty Aa:
 ……..(11)
……..(11)
Zmniejszenie częstości heterozygot Aa następuje, jak już wcześniej udowodniono, w wyniku identycznego wzrostu częstości homozygot dominujących AA i recesywnych aa. Na przykład, wzrost częstości homozygot recesywnych aa jest równy:
 ……..(12)
……..(12)
gdzie redukcja częstości heterozygot Aa względem panmikrycznego drzewa genealogicznego wg (7) i (11) jest równa. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) Stosując (11) i (12) do aktualizacji (7) dla przypadków chowu wsobnego znajdujemy rozkład genotypów (10) w chromosomach Х w córkach wsobnego drzewa genealogicznego.
W następnym pokoleniu częstość alleli recesywnych a u kobiet jest równa:
 ……..(13)
……..(13)
To w pełni odpowiada tej samej częstości przy braku chowu wsobnego, tzn. następuje przywrócenie równowagi Hardy’ego – Weinberga lub dokładniej zbliżenie się do tej równowagi.
Zależność (7) i (13) pokazuje jako całość, że częstości alleli w drzewie genealogicznym przy braku chowu wsobnego nie zmieniają się. Następuje jedynie redystrybucja alleli. Część alleli opuszcza heterozygoty i przechodzi na homozygoty.