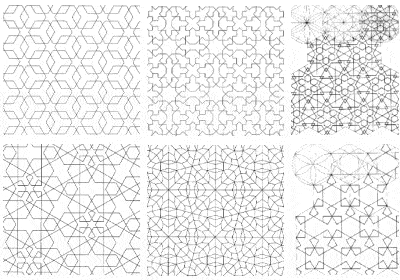
Kilka przykładów złożonych symetrii stosowanych w islamskiej dekoracji świątyń
Imperium islamskie założone w Persji, na Bliskim Wschodzie, w Azji Środkowej, Afryce Północnej, Iberii i części Indii od VIII w. wniosło znaczący wkład w matematykę. Byli oni w stanie czerpać i łączyć matematyczne osiągnięcia zarówno Grecji, jak i Indii.
Jedną z konsekwencji islamskiego zakazu przedstawiania postaci ludzkiej było szerokie zastosowanie złożonych wzorów geometrycznych do dekoracji budynków, podnosząc matematykę do rangi sztuki. W rzeczywistości, z czasem, muzułmańscy artyści odkryli wszystkie różne formy symetrii, które mogą być przedstawione na dwuwymiarowej powierzchni.
Sam Qu’ran zachęcał do gromadzenia wiedzy, a złoty wiek islamskiej nauki i matematyki kwitł w okresie średniowiecza od 9 do 15 wieku. Dom Mądrości został założony w Bagdadzie około 810 roku i niemal natychmiast rozpoczęto pracę nad tłumaczeniem na arabski głównych greckich i indyjskich dzieł matematycznych i astronomicznych.
Wybitny perski matematyk Muhammad Al-Khwarizmi był wczesnym dyrektorem Domu Mądrości w IX wieku i jednym z największych wczesnych matematyków muzułmańskich. Być może najważniejszym wkładem Al-Khwarizmiego do matematyki było jego silne poparcie dla hinduskiego systemu liczbowego (1-9 i 0), który uznał za posiadający moc i skuteczność potrzebną do zrewolucjonizowania islamskiej (a później zachodniej) matematyki, i który został wkrótce przyjęty przez cały świat islamski, a później także przez Europę.
Innym ważnym wkładem Al-Khwarizmiego była algebra, wprowadził on podstawowe algebraiczne metody „redukcji” i „równoważenia” oraz przedstawił wyczerpujący opis rozwiązywania równań wielomianowych do drugiego stopnia. W ten sposób przyczynił się do stworzenia potężnego abstrakcyjnego języka matematycznego używanego do dziś na całym świecie i umożliwił znacznie bardziej ogólny sposób analizowania problemów innych niż tylko konkretne problemy rozważane wcześniej przez Hindusów i Chińczyków.
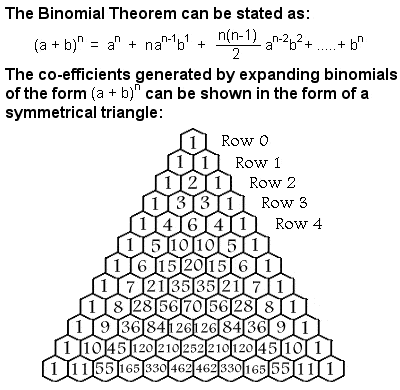
Twierdzenie dwumianowe
W X wieku perski matematyk Muhammad Al-Karadżi pracował nad dalszym rozszerzeniem algebry, uwalniając ją od jej geometrycznego dziedzictwa, i wprowadził teorię rachunku algebraicznego. Al-Karadżi był pierwszym, który użył metody dowodu przez indukcję matematyczną do udowodnienia swoich wyników, udowadniając, że pierwsze stwierdzenie w nieskończonej sekwencji stwierdzeń jest prawdziwe, a następnie udowadniając, że jeśli jakiekolwiek stwierdzenie w sekwencji jest prawdziwe, to jest również następne.
Twierdzenie dwumianowe
Między innymi, Al-Karadżi użył indukcji matematycznej do udowodnienia twierdzenia dwumianowego. Dwumian jest prostym rodzajem wyrażenia algebraicznego, które ma tylko dwa warunki, na których operuje się tylko dodawaniem, odejmowaniem, mnożeniem i dodatnimi wykładnikami liczb całkowitych, takimi jak (x + y)2. Współczynniki potrzebne do rozwinięcia dwumianu tworzą trójkąt symetryczny, nazywany zwykle trójkątem Pascala od nazwiska francuskiego matematyka Blaise’a Pascala z XVII wieku, choć wielu innych matematyków studiowało go wieki przed nim w Indiach, Persji, Chinach i Włoszech, w tym Al-Karadżi.
Jakieś sto lat po Al-Karadżim, Omar Chajjam (być może bardziej znany jako poeta i autor „Rubajjatu”, ale ważny matematyk i astronom w swoim własnym prawie) uogólnił indyjskie metody wyodrębniania pierwiastków kwadratowych i sześciennych, aby włączyć czwarte, piąte i wyższe korzenie na początku XII wieku. Przeprowadził systematyczną analizę problemów sześciennych, ujawniając, że w rzeczywistości istniało kilka różnych rodzajów równań sześciennych. Chociaż faktycznie udało mu się rozwiązać równania sześcienne, i chociaż zwykle przypisuje mu się zidentyfikowanie podstaw geometrii algebraicznej, został powstrzymany od dalszych postępów przez niezdolność do oddzielenia algebry od geometrii, a czysto algebraiczna metoda rozwiązywania równań sześciennych musiała poczekać kolejne 500 lat i włoskich matematyków del Ferro i Tartaglia.
Trygonometria sferyczna
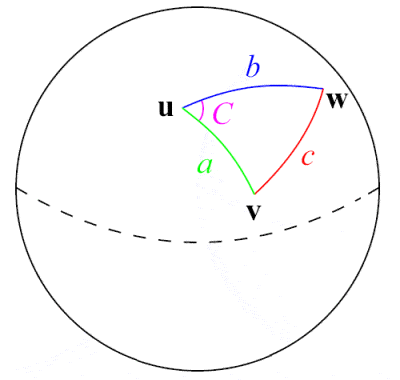
Al-Tusi był pionierem w dziedzinie trygonometrii sferycznej
W XIII wieku perski astronom, naukowiec i matematyk Nasir Al-Din Al-Tusi był prawdopodobnie pierwszym, który potraktował trygonometrię jako oddzielną dyscyplinę matematyczną, odrębną od astronomii. Opierając się na wcześniejszej pracy greckich matematyków, takich jak Menelaos z Aleksandrii i indyjskiej pracy nad funkcją sinus, dał pierwszą obszerną ekspozycję trygonometrii sferycznej, w tym listę sześciu różnych przypadków trójkąta prostego w trygonometrii sferycznej. Jednym z jego głównych wkładów matematycznych było sformułowanie słynnego prawa sinusów dla trójkątów płaskich, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), chociaż prawo sinusów dla trójkątów sferycznych zostało odkryte wcześniej przez Persów Abul Wafa Buzjani i Abu Nasr Mansur w X wieku.
Inni średniowieczni matematycy muzułmańscy godni uwagi to między innymi:
- Arab Thabit ibn Qurra z IX wieku, który opracował ogólny wzór pozwalający na wyprowadzenie liczb wymiernych, odkryty znacznie później zarówno przez Fermata jak i Kartezjusza (liczby wymierne to pary liczb, dla których suma dzielników jednej liczby jest równa drugiej, np.np. dzielniki właściwe liczby 220 to 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 i 110, których suma wynosi 284; a dzielniki właściwe liczby 284 to 1, 2, 4, 71 i 142, których suma wynosi 220);
- 10-wieczny arabski matematyk Abul Hasan al-Uqlidisi, który napisał najwcześniejszy zachowany tekst pokazujący pozycyjne użycie cyfr arabskich, a w szczególności użycie liczb dziesiętnych zamiast ułamków (np.g. 7.375 zamiast 73⁄8);
- X w. arabski geometra Ibrahim ibn Sinan, który kontynuował badania Archimedesa nad obszarami i objętościami, a także nad stycznymi do okręgu;
- 11-wieczny perski Ibn al-Haytham (znany również jako Alhazen), który oprócz swojej przełomowej pracy w dziedzinie optyki i fizyki, ustanowił początki związku między algebrą i geometrią oraz opracował to, co jest obecnie znane jako „problem Alhazena” (był pierwszym matematykiem, który wyprowadził wzór na sumę czwartych potęg, używając metody, która jest łatwo generalizowalna); i
- XIII-wieczny Pers Kamal al-Din al-Farisi, który zastosował teorię przekrojów stożkowych do rozwiązywania problemów optycznych, a także kontynuował prace z zakresu teorii liczb, takie jak liczby wymierne, faktoryzacja i metody kombinatoryczne;
- XIII-wieczny Marokańczyk Ibn al-Banna al-Marrakushi, którego prace obejmowały takie tematy jak obliczanie pierwiastków kwadratowych i teoria ułamków ciągłych, jak również odkrycie pierwszej nowej pary liczb wymiernych od czasów starożytnych (17,296 i 18,416, później ponownie odkryte przez Fermata) oraz pierwsze użycie notacji algebraicznej od czasów Brahmagupty.
Pod dławiącym wpływem tureckiego Imperium Osmańskiego od XIV lub XV wieku, matematyka islamska uległa stagnacji, a dalszy rozwój przeniósł się do Europy.
| << Powrót do Madhavy | Dalej do Al-.Khwarizmi >> |