Powrót do Indeksu Lekcji | Wykonaj Lekcje w Kolejności | Strona przyjazna do drukowania
Twierdzenie o współczynnikach
Twierdzenie o współczynnikach jest wynikiem Twierdzenia o Resztkach i opiera się na tym samym rozumowaniu. Jeśli nie czytałeś lekcji o Twierdzeniu Reszty, przejrzyj najpierw ten temat, a potem wróć tutaj.
Jak wskazuje Twierdzenie Reszty, jeśli podzielisz wielomian p(x) przez czynnik x – a tego wielomianu, otrzymasz resztę zerową. Spójrzmy jeszcze raz na to wyrażenie algorytmu dzielenia wielomianu:
Ogłoszenie
p(x) = (x – a)q(x) + r(x)
Jeśli x – a jest rzeczywiście czynnikiem p(x), to reszta po dzieleniu przez x – a będzie równa zero. Czyli:
p(x) = (x – a)q(x)
Z punktu widzenia Twierdzenia o Resztkach oznacza to, że jeśli x – a jest czynnikiem p(x), to reszta po dzieleniu syntetycznym przez
x = a będzie równa zero.
Twierdzenie o Czynnikach jest odwrotnością Twierdzenia o Resztkach: Jeśli syntetycznie podzielimy wielomian przez x = a i otrzymamy zerową resztę, to nie tylko x = a jest zerem wielomianu (dzięki uprzejmości Twierdzenia o Resztkach), ale x – a jest również czynnikiem wielomianu (dzięki uprzejmości Twierdzenia o Czynnikach).
Tak jak w przypadku Twierdzenia o Resztkach, chodzi tu o to, by nie wykonywać długiego dzielenia danego wielomianu przez dany czynnik. To Twierdzenie nie powtarza tego, co już wiesz, ale stara się uprościć Twoje życie. Kiedy staniesz przed zadaniem związanym z Twierdzeniem o czynnikach, zastosujesz dzielenie syntetyczne, a następnie sprawdzisz, czy reszta jest równa zero.
- Użyj Twierdzenia o Czynnikach, aby określić, czy x – 1 jest czynnikiem
f (x) = 2×4 + 3×2 – 5x + 7.
- Korzystając z twierdzenia o współczynnikach, sprawdź, czy x + 4 jest współczynnikiem
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16. - Korzystając z faktu, że -2 i 1/3 są zerami wielomianu f (x) = 3×4 + 5×3 + x2 + 5x – 2, obliczamy czynnik całkowity tego wielomianu. Copyright © Elizabeth Stapel 2002-2011 All Rights Reserved
Aby x – 1 był czynnikiem f (x) = 2×4 + 3×2 – 5x + 7, Twierdzenie o Czynnikach mówi, że x = 1 musi być zerem f (x). Aby sprawdzić, czy x – 1 jest czynnikiem, najpierw ustawię x – 1 równe zero i rozwiążę, aby znaleźć proponowane zero, x = 1. Następnie użyję dzielenia syntetycznego, aby podzielić f (x) przez x = 1. Ponieważ nie ma pierwiastka sześciennego, będę uważał, aby pamiętać o wstawieniu „0” w pierwszym wierszu podziału syntetycznego, aby reprezentować pominiętą potęgę x w 2×4 + 3×2 – 5x + 7:
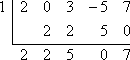
Ponieważ reszta nie jest równa zero, to Twierdzenie o czynnikach mówi, że:
x – 1 nie jest czynnikiem f (x).
Jeśli x + 4 jest współczynnikiem, to (ustawiając ten współczynnik na zero i rozwiązując) x = -4 jest pierwiastkiem. Aby przeprowadzić wymaganą weryfikację, muszę sprawdzić, że gdy zastosuję dzielenie syntetyczne na f (x), przy x = -4, otrzymam zerową resztę:
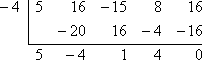
Reszta jest równa zero, więc Twierdzenie o czynnikach mówi, że:
x + 4 jest czynnikiem 5×4 + 16×3 – 15×2 + 8x + 16.
W praktyce, Twierdzenie o współczynnikach stosuje się przy faktoryzacji wielomianów „zupełnej”. Zamiast próbować różnych czynników za pomocą długiego dzielenia, użyjemy dzielenia syntetycznego i Twierdzenia o współczynnikach. Za każdym razem, gdy dzielimy przez liczbę (będącą potencjalnym pierwiastkiem wielomianu) i otrzymujemy zerową resztę z dzielenia syntetycznego, oznacza to, że liczba ta rzeczywiście jest pierwiastkiem, a zatem „x minus liczba” jest czynnikiem. Następnie kontynuujemy dzielenie z otrzymanym mniejszym wielomianem, aż otrzymamy czynnik liniowy (więc znaleźliśmy wszystkie czynniki) lub kwadratowy (do którego możemy zastosować Wzór na kwadrat).
Jeśli x = -2 jest zerem, to x + 2 = 0, więc x + 2 jest współczynnikiem. Podobnie, jeśli x = 1/3 jest zerem, to x – 1/3 = 0, więc x – 1/3 jest czynnikiem. Dając mi dwa zera, dali mi również dwa czynniki: x + 2 i x – 1/3.
Ponieważ zacząłem od wielomianu czwartego stopnia, to po rozdzieleniu tych dwóch danych czynników zostanie mi kwadratura. Mogę go rozwiązać za pomocą wzoru na kwadrat lub innej metody.
Twierdzenie o czynnikach mówi, że nie muszę wykonywać długiego dzielenia ze znanymi czynnikami x + 2 i x – 1/3. Zamiast tego mogę użyć syntetycznego podziału z powiązanymi zerami -2 i 1/3. Oto, co otrzymam, gdy wykonam pierwszy podział z x = -2:
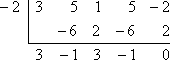
Reszta wynosi zero, co jest oczekiwane, ponieważ powiedzieli mi na początku, że -2 było znanym zerem wielomianu. Zamiast zaczynać od nowa z oryginalnym wielomianem, będę teraz pracował na pozostałym czynniku wielomianu 3×3 – x2 + 3x – 1 (z dolnego wiersza syntetycznego podziału). Podzielę go przez drugie dane zero, x = 1/3:
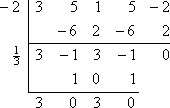
Zostaje mi kwadratura 3×2 + 3, którą mogę rozwiązać:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Jeśli zerami są x = -i oraz x = i, to czynnikami są x – (-i) oraz x – (i), czyli x + i oraz x – i. I need to remember that I divided off a „3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. „The Factor Theorem.” Purplemath. Available from 2016
|