Wady używania zmiennych instrumentalnych do wykazania przyczynowości
Jako przykład, rozważmy kwestię oszacowania wpływu wykształcenia na zarobki. Najprostsza technika estymacji, zwykłe najmniejsze kwadraty (OLS), generuje szacunki wskazujące, że jeden dodatkowy rok edukacji jest związany z zarobkami wyższymi o 6-10%. Pozytywna zależność może jednak wynikać z autoselekcji do edukacji, tzn. osoby, które mogą najwięcej zyskać dzięki wyższemu wykształceniu, są bardziej skłonne do pozostania na rynku pracy. Będzie tak na przykład w przypadku, gdy uczniowie o większych zdolnościach łatwiej się uczą i prawdopodobnie i tak otrzymywaliby wyższe wynagrodzenie. W związku z tym dodatnia korelacja zaobserwowana między latami edukacji a płacami częściowo odzwierciedlałaby premię za zdolności, a nie mogłaby być interpretowana jako zyski z dodatkowego roku edukacji, jak zamierzano. Szacunki OLS nie dostarczałyby zatem informacji o skutkach polityki mającej na celu zwiększenie liczby lat edukacji. Ten problem nazywany jest „błędem pominiętej zmiennej”. Występuje on, gdy zmienna (taka jak zdolność), która nie jest obserwowana przez badacza, jest skorelowana zarówno z leczeniem (więcej edukacji), jak i z wynikiem (zarobki). Kierunek (przeszacowanie lub niedoszacowanie) i wielkość błędu systematycznego w oszacowaniach OLS jest funkcją znaku i siły korelacji.
W tym przykładzie, randomizowana próba kontrolna (RCT), która pociągnęłaby za sobą losowe przydzielanie edukacji jednostkom i obserwowanie różnic w ich zarobkach przez całe życie, jest po prostu niewykonalna ze względów etycznych. Jednak niektóre naturalne lub quasi-naturalne eksperymenty mogą zbliżyć się do zmiany wyborów edukacyjnych dla niektórych grup osób i jako takie mogą być wykorzystane jako instrumenty. Jednym z takich naturalnych eksperymentów jest zmiana ustawowego minimalnego wieku, w którym uczniowie mogą opuścić szkołę (wiek zakończenia nauki). Tego typu zmiana dotyczy wszystkich uczniów, niezależnie od ich zdolności. Działa zatem jak zewnętrzny szok, na który nie może wpłynąć indywidualny uczeń.
W wielu krajach obowiązują przepisy określające wiek, w którym uczniowie mogą opuścić system edukacji. Na przykład, powiedzmy, że dziecko może opuścić szkołę w ostatnim dniu roku szkolnego, jeśli do końca sierpnia skończy 14 lat. Załóżmy teraz, że przepisy zostały zmienione, tak że dzieci muszą mieć 15 lat do końca sierpnia, aby móc opuścić szkołę. Dzieci, które chciały opuścić szkołę w wieku 14 lat, nie mogą tego zrobić i muszą pozostać na dodatkowy rok nauki. Przy (silnym) założeniu, że dzieci objęte oboma ustawodawstwami są podobne i mają podobne warunki na rynku pracy, zmiana ustawodawstwa tworzy quasi-naturalny eksperyment: niezależnie od ich zdolności, niektóre osoby będą dotknięte zmianą wieku zakończenia nauki i będą musiały pozostać na dodatkowy rok nauki, podczas gdy uczniowie o podobnych preferencjach z poprzedniej kohorty nie będą. Gdyby badacze wiedzieli, kto chce opuścić szkołę w wieku 14 lat, mogliby porównać wyniki osób, które opuściły szkołę w wieku 14 lat, z wynikami osób, które zostały zmuszone do pozostania do 15 roku życia. Ta prosta różnica byłaby wtedy efektem przyczynowym pozostawania w szkole między 14 a 15 rokiem życia. Niestety, dane obserwacyjne nie pozwalają nam na identyfikację osób, na których wybór edukacyjny wpłynęła reforma; tak więc, zgodnie z nowymi przepisami, osoby, które chciały opuścić szkołę w wieku 15 lat są nie do odróżnienia od tych, które chciały opuścić szkołę w wieku 14 lat, ale musiały pozostać w niej jeszcze przez rok. Tym niemniej reforma zmienia prawdopodobieństwo pozostania w szkole, a zatem może być użyta jako instrument, ponieważ wpływa na prawdopodobieństwo leczenia (kolejny rok nauki) bez wpływu na wynik zainteresowania (np. zarobki).
W 1947 r. zmiana legislacyjna w Wielkiej Brytanii podniosła minimalny wiek ukończenia szkoły z 14 do 15 lat, wpływając na dzieci urodzone w 1933 r. i później. Ta zmiana prawa daje możliwość oceny wpływu (dodatkowej) nauki szkolnej na zarobki. Na rysunku 1, panel A pokazuje, że reforma wpłynęła zarówno na frakcję dzieci kończących szkołę przy najbliższej okazji (lewy wykres), jak i na całkowitą liczbę ukończonych szkół (prawy wykres). Szacunki wskazują, że reforma zwiększyła średnią liczbę lat nauki szkolnej dla mężczyzn o 0,397 roku. To oszacowanie wpływu reformy (IV) na leczenie (edukację) jest znane jako „regresja pierwszego stopnia”. Jeśli wykształcenie ma jakikolwiek przyczynowy wpływ na zarobki, powinniśmy zaobserwować, że średnie zarobki osób dotkniętych reformą są również wyższe. Tak rzeczywiście jest, co widać w panelu B na wykresie 1, który przedstawia średnie logarytmy zarobków dla mężczyzn. W tym szeregu widać wyraźne załamanie w 1933 r., którego wielkość sugeruje, że osoby dotknięte reformą zarabiają średnio o 1,2% więcej. To drugie oszacowanie wpływu reformy (IV) na wynik (zarobki) jest znane jako „oszacowanie w formie zredukowanej”. Prosta strategia IV, w tym przypadku wykorzystująca instrument binarny, który przyjmuje tylko dwie wartości (1 dla wpływu reformy i 0 dla braku wpływu reformy), jest stosunkiem zredukowanej formy oszacowania do oszacowania pierwszego etapu. (W tym przypadku efekt przyczynowy dodatkowego wykształcenia na zarobki wyniósłby 0,012/0,397 = 0,030, a więc około 3%.
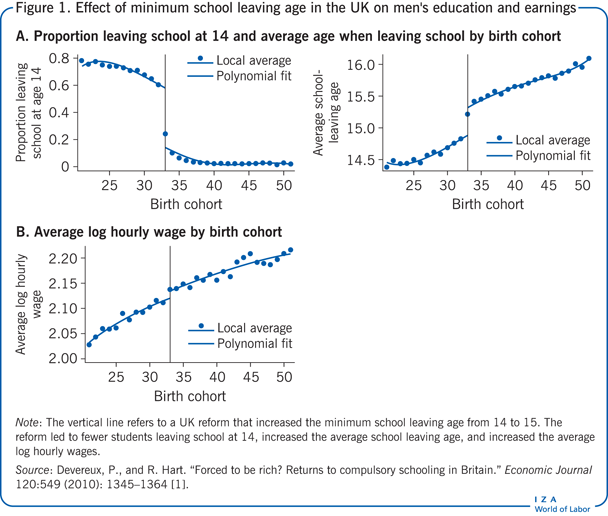
Intuicja tego podejścia jest taka, że efekt jednego dodatkowego roku edukacji na płace jest w zasadzie efektem reformy (IV) na płace (wynik) – który jest podany w formie zredukowanej – przeskalowany przez efekt, który reforma ma na lata edukacji (leczenie) – co jest tym, czego dotyczy estymacja pierwszego etapu. Jeżeli instrument jest „istotny”, tzn. ma wpływ na edukację (leczenie) i jeżeli instrument wpływa na płace „wyłącznie” poprzez swój wpływ na edukację, wówczas oszacowania IV można interpretować jako efekt przyczynowy leczenia na wynik. Te dwa warunki nazywane są „istotnością instrumentu” i „ograniczeniem wykluczenia”
Podsumowując, kiedy nieobserwowalna zmienna, taka jak zdolność, koreluje zarówno z leczeniem, jak i z wynikiem, proste oszacowanie, takie jak OLS, będzie nieobiektywne z powodu samoselekcji do leczenia. Podobnie, jeśli zmienna traktowania jest mierzona z błędem, oszacowanie OLS będzie obarczone błędem w kierunku zera. Jednakże, szacunek przyczynowego wpływu leczenia na wynik może być uzyskany, jeżeli można znaleźć wiarygodny instrument. Wiarygodny instrument musi spełniać dwa warunki:
-
Relewantność: instrument musi wpływać na prawdopodobieństwo leczenia. W regresji leczenia na instrument, znanej również jako równanie pierwszego stopnia, współczynnik na IV musi być wystarczająco silny.
-
Wyłączenie ograniczenia: instrument wpływa na wynik wyłącznie poprzez swój wpływ na leczenie.
Jeśli taki IV może być znaleziony (tj. zarówno istotność, jak i ograniczenie wykluczające są spełnione), wówczas można zastosować strategię IV, aby odzyskać efekt przyczynowy leczenia na wynik.
Poprzedni przykład przedstawiał estymatę Walda, tj. stosunek estymat z dwóch regresji: estymata w formie zredukowanej, pochodząca z regresji wyniku na instrumencie oraz estymata pierwszego stopnia, pochodząca z regresji leczenia na instrumencie. Można to łatwo obliczyć, gdy instrument przyjmuje tylko dwie wartości. W bardziej ogólnym przypadku oblicza się tak zwaną estymatę „dwóch etapów najmniejszych kwadratów” (2SLS), przy czym przewidywania dotyczące traktowania z równania pierwszego etapu są wykorzystywane w regresji wyniku na traktowaniu, a nie rzeczywista wartość traktowania. Jako takie, tylko wariancja w traktowaniu pochodząca z instrumentu jest wykorzystywana do wyjaśnienia wariancji w wyniku. W ten sposób rozwiązuje się problem tendencyjności selekcji własnej. W przypadku instrumentu binarnego (dwuwartościowego), oszacowania Walda i 2SLS będą identyczne (zob. na przykład , ). Jednakże trudność nie polega na implementacji takiego oszacowania 2SLS, wszystkie pakiety statystyczne mogą obliczyć oszacowania IV, ale na (a) znalezieniu ważnego instrumentu i (b) interpretacji wyników. Dyskusja będzie się teraz koncentrować na tych dwóch punktach.