Viteza undei pe o coardă sub tensiune
Pentru a vedea cum viteza unei unde pe o coardă depinde de tensiune și de densitatea liniară, considerați un impuls trimis pe o coardă întinsă (Figura \(\PageIndex{1}\)). Atunci când coarda întinsă se află în repaus în poziția de echilibru, tensiunea din coardă \(F_T\) este constantă. Se consideră un mic element al șirului cu o masă egală cu \(\Delta m = \mu \Delta x\). Elementul de masă este în repaus și în echilibru, iar forța de întindere de o parte și de alta a elementului de masă este egală și opusă.
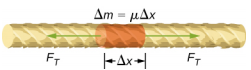
Dacă se smulge o coardă sub tensiune, o undă transversală se deplasează în direcția x pozitivă, așa cum se arată în figura \(\PageIndex{2}\). Elementul de masă este mic, dar este mărit în figură pentru a-l face vizibil. Elementul de masă mic oscilează perpendicular pe mișcarea undei ca urmare a forței de refacere furnizate de coardă și nu se deplasează în direcția x. Tensiunea FT din coardă, care acționează în direcția x pozitivă și negativă, este aproximativ constantă și este independentă de poziție și timp.
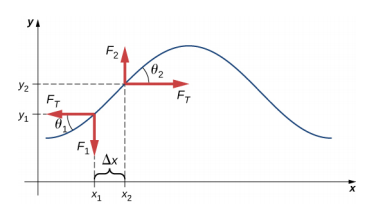
Să presupunem că înclinarea coardei deplasate în raport cu axa orizontală este mică. Forța netă asupra elementului de coardă, care acționează paralel cu coarda, este suma dintre tensiunea din coardă și forța de restabilire. Componentele x ale forței de întindere se anulează, astfel încât forța netă este egală cu suma componentelor y ale forței. Mărimea componentei x a forței este egală cu forța orizontală de întindere a coardei \(F_T\), așa cum se arată în figura \(\PageIndex{2}\). Pentru a obține componentele y ale forței, rețineți că tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}\) și \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}\). \(\(\tan \theta\) este egală cu panta unei funcții într-un punct, care este egală cu derivata parțială a lui y în raport cu x în acel punct. Prin urmare, \(\(\frac{F_{1}}{F_{T}}\) este egală cu panta negativă a șirului în x1 și \(\frac{F_{2}}{F_{T}}\) este egală cu panta șirului în x2:
Forța netă este asupra elementului de masă mică poate fi scrisă ca
\ldotp\\]
Utilizând a doua lege a lui Newton, forța netă este egală cu masa înmulțită cu accelerația. Densitatea liniară a coardei µ este masa pe lungimea coardei, iar masa porțiunii de coardă este \(\mu \Delta\)x,
\ = \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\drept) \ldotp\]
Divizând cu FT\(\Delta\)x și luând limita pe măsură ce \(\Delta\)x se apropie de zero,
\}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\frac \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]
Reamintim că ecuația de undă liniară este
Prin urmare,
Soluționând pentru \(v\), vedem că viteza undei pe o coardă depinde de tensiune și de densitatea liniară
Viteza unei unde pe o coardă sub tensiune
Viteza unui impuls sau a unei unde pe o coardă sub tensiune poate fi găsită cu ajutorul ecuației
unde \(F_T\) este tensiunea din coardă și \(µ\) este masa pe lungimea coardei.
Exemplu 16.5: Viteza de undă a unui arc de chitară
La o chitară cu șase corzi, coarda cu E mare are o densitate liniară de \(\mu_{High\; E}\) = 3,09 x 10-4 kg/m, iar coarda cu E mic are o densitate liniară de \(\mu_{Low\; E}\) = 5,78 x 10-3 kg/m. (a) Dacă coarda cu E mare este ciupită, producând o undă în coardă, care este viteza undei dacă tensiunea coardei este de 56,40 N? (b) Densitatea liniară a coardei E joase este de aproximativ 20 de ori mai mare decât cea a coardei E înalte. Pentru ca valurile să se deplaseze prin coarda E scăzut cu aceeași viteză a valurilor ca și în cazul coardei E ridicat, ar trebui ca tensiunea să fie mai mare sau mai mică decât în cazul coardei E ridicat? Care ar fi tensiunea aproximativă? (c) Calculați tensiunea coardei E scăzut necesară pentru aceeași viteză a undelor.
Strategie
- Viteza undei poate fi găsită din densitatea liniară și tensiunea \(v = \sqrt{\frac{F_{T}}{\mu}}\).
- Din ecuația v = \(\sqrt{\frac{F_{T}}{\mu}}\), dacă densitatea liniară este crescută cu un factor de aproape 20, tensiunea ar trebui să fie crescută cu un factor de 20.
- Cunoscând viteza și densitatea liniară, ecuația vitezei poate fi rezolvată pentru forța de tensiune FT = \(\mu\)v2.
Soluție
- Utilizați ecuația vitezei pentru a găsi viteza: $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\; N}{3.09 \times 10^{-4}\; kg/m}}} = 427.23\; m/s \ldotp$$
- Tensiunea ar trebui să fie mărită cu un factor de aproximativ 20. Tensiunea ar fi puțin mai mică de 1128 N.
- Utilizați ecuația vitezei pentru a găsi tensiunea reală: $$F_{T} = \mu v^{2} = (5,78 \times 10^{-3}\; kg/m)(427,23\; m/s)^{2} = 1055,00\; N \ldotp$$$
- Această soluție se află la 7% din aproximație.
Semnificație
Notele standard ale celor șase corzi (Mi mare, Si, Sol, Re, La, Mi mic) sunt acordate să vibreze la frecvențele fundamentale (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz și 82,41 Hz) atunci când sunt ciupite. Frecvențele depind de viteza undelor pe coardă și de lungimea de undă a acestora. Cele șase corzi au densități liniare diferite și sunt „acordate” prin modificarea tensiunilor din corzi. Vom vedea în Interferența undelor că lungimea de undă depinde de lungimea corzilor și de condițiile la limită. Pentru a cânta alte note decât notele fundamentale, lungimile corzilor sunt modificate prin apăsarea corzilor.
Exercițiu 16.5
Viteza unei unde pe o coardă depinde de tensiune și de densitatea liniară a masei. Dacă tensiunea este dublată, ce se întâmplă cu viteza undelor pe coardă?
.