Vantagens de usar variáveis instrumentais para demonstrar a causalidade
Como exemplo, considere a questão da estimação do efeito da educação sobre os ganhos. A técnica mais simples de estimação, os mínimos quadrados comuns (OLS), gera estimativas indicando que um ano adicional de escolaridade está associado a ganhos que são 6-10% maiores . No entanto, a relação positiva pode ser impulsionada pela auto-seleção na educação; ou seja, os indivíduos que têm mais a ganhar com mais educação têm mais probabilidade de ficar. Este será o caso, por exemplo, se os alunos com maior capacidade acharem mais fácil estudar, e provavelmente receberiam salários mais altos de qualquer forma. Como tal, a correlação positiva observada entre anos de educação e salários reflectiria parcialmente o prémio de capacidade, e não poderia ser interpretada como o retorno de um ano adicional de educação, como pretendido. As estimativas da OLS não seriam, portanto, informativas sobre o efeito de uma política destinada a aumentar os anos de escolaridade. Este problema é chamado de “viés variável omitido”. Ocorre quando uma variável (como a capacidade) que não é observada pelo pesquisador está correlacionada tanto com o tratamento (mais escolaridade) quanto com o resultado (ganhos). A direção (sobre ou subestimação) e o tamanho do viés nas estimativas de OLS é uma função do sinal e da força das correlações.
Neste exemplo, um ensaio de controle aleatório (RCT), que implicaria em alocar a educação aleatoriamente aos indivíduos e observar as diferenças em seus salários ao longo de sua vida, simplesmente não é viável por razões éticas. Contudo, algumas experiências naturais ou quase naturais podem chegar perto de alterar a escolha educacional para alguns grupos de indivíduos, e como tal, podem ser usadas como instrumentos. Uma dessas experiências naturais é uma mudança na idade mínima legal em que os alunos podem deixar a escola (idade de deixar a escola). Este tipo de mudança afecta todos os alunos, independentemente da sua capacidade. Portanto, age como um choque externo que não pode ser influenciado pelo aluno individual.
Numeros países têm legislação que estipula a idade em que os alunos podem deixar o sistema educacional. Por exemplo, digamos que uma criança pode deixar a escola no último dia do ano lectivo se tiver 14 anos até ao final de Agosto. Vamos supor agora que a legislação é alterada, de modo que as crianças têm de ter 15 anos até ao final de Agosto para poderem deixar a escola. As crianças que queriam deixar a escola aos 14 anos são impedidas de o fazer e têm de permanecer por mais um ano de escolaridade. Sob o (forte) pressuposto de que as crianças sob as duas legislações são semelhantes e enfrentam condições de mercado de trabalho semelhantes, a alteração da legislação cria uma experiência quase natural: independentemente da sua capacidade, alguns indivíduos serão afectados pela alteração da idade de abandono escolar e terão de permanecer por mais um ano de escolaridade, enquanto os alunos com preferências semelhantes da coorte anterior não o serão. Se os investigadores soubessem quem queria deixar a escola aos 14 anos, poderiam comparar os resultados dos indivíduos que deixaram a escola aos 14 anos com os resultados dos indivíduos que foram forçados a ficar até aos 15 anos. Esta simples diferença seria então o efeito causal de permanecer na escola entre os 14 e 15 anos de idade. Infelizmente, os dados observacionais não nos permitem identificar os indivíduos cuja escolha educacional foi afetada pela reforma; assim, sob a nova legislação, os indivíduos que queriam sair da escola aos 15 anos são indistinguíveis daqueles que queriam sair aos 14 anos, mas tiveram que permanecer por mais um ano. O que a reforma faz, no entanto, é alterar a probabilidade de permanecer na escola, podendo assim ser usada como um instrumento, uma vez que afecta a probabilidade de tratamento (mais um ano de escolaridade) sem afectar o resultado dos juros (por exemplo, os rendimentos).
Em 1947, uma alteração legislativa no Reino Unido aumentou a idade mínima de abandono escolar de 14 para 15 anos, afectando as crianças nascidas em 1933 e depois. Esta mudança na lei oferece uma oportunidade de avaliar o efeito da escolaridade (adicional) sobre os rendimentos. Na Figura 1, o painel A mostra que a reforma afectou tanto a fracção de crianças que abandonaram a escola na primeira oportunidade (gráfico da esquerda) como o total de escolaridade concluída (gráfico da direita). As estimativas indicam que a reforma aumentou a média de anos de escolaridade dos homens em 0,397 anos. Esta estimativa do efeito da reforma (o IV) sobre o tratamento (educação) é conhecida como a “regressão da primeira fase”. Se a educação tem algum efeito causal sobre os rendimentos, devemos observar que os rendimentos médios dos indivíduos afectados pela reforma também são mais elevados. Este é, de facto, o caso como mostra o painel B da Figura 1, que reporta os ganhos médios em log para os homens. Esta série mostra uma clara ruptura em 1933, cuja magnitude implica que os indivíduos afetados pela reforma ganham, em média, 1,2% mais do que os homens. Esta segunda estimativa do efeito da reforma (o IV) sobre o resultado (rendimentos) é conhecida como a “estimativa de forma reduzida”. Uma estratégia simples de IV, neste caso utilizando um instrumento binário que assume apenas dois valores (1 por ser afectado pela reforma, e 0 por não ser afectado pela reforma), é o rácio da estimativa da forma reduzida ao longo da estimativa da primeira fase. (Esta razão também é conhecida como a estimativa Wald.) Neste caso, o efeito causal da educação adicional sobre os ganhos seria de 0,012/0,397 = 0,030 e, portanto, cerca de 3%.
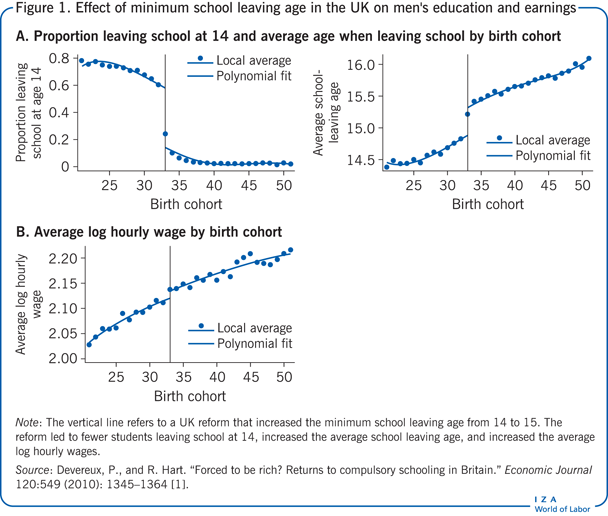
A intuição desta abordagem é que o efeito de mais um ano de educação sobre os salários é basicamente o efeito da reforma (o IV) sobre os salários (o resultado) – que é dado na forma reduzida – que é ampliado pelo efeito que a reforma tem sobre os anos de educação (o tratamento) – que é o que é a estimativa da primeira fase. Se o instrumento é “relevante”, ou seja, tem um efeito na educação (o tratamento), e se o instrumento afecta os salários “exclusivamente” através do seu efeito na educação, então as estimativas da IV podem ser interpretadas como o efeito causal do tratamento sobre o resultado. Estas duas condições são chamadas de “relevância do instrumento” e “restrição de exclusão”
Para resumir, quando uma variável não observada como a habilidade correlaciona tanto com o tratamento quanto com o resultado, uma estimativa simples como a OLS será tendenciosa devido à auto-seleção no tratamento. Da mesma forma, se a variável de tratamento for medida com erro, a estimativa da OLS será tendenciosa para zero. Entretanto, uma estimativa causal de um tratamento sobre um resultado pode ser recuperada se um instrumento confiável puder ser encontrado. Um instrumento credível deve satisfazer duas condições:
- p>Relevância: o instrumento deve afetar a probabilidade de tratamento. Numa regressão do tratamento no instrumento, também conhecida como equação da primeira etapa, o coeficiente sobre o IV deve ser suficientemente forte.
-
Restrição à exclusão: o instrumento afecta o resultado exclusivamente através do seu efeito sobre o tratamento.
Se um tal IV puder ser encontrado (ou seja Se for possível encontrar um tal IV (ou seja, tanto a relevância quanto a restrição de exclusão são cumpridas), então uma estratégia de IV pode ser implementada para recuperar um efeito causal do tratamento no resultado.
O exemplo anterior apresentou a estimativa de Wald, ou seja, a razão das estimativas de duas regressões: a estimativa da forma reduzida, proveniente de uma regressão do resultado no instrumento; e a estimativa da primeira etapa, proveniente de uma regressão do tratamento no instrumento. Isto pode ser facilmente calculado quando o instrumento leva apenas dois valores. No caso mais geral, uma estimativa chamada de “dois estágios menos quadrados” (2SLS) será computada, onde as previsões do tratamento da equação do primeiro estágio são usadas em uma regressão do resultado sobre o tratamento, ao invés do valor verdadeiro do tratamento. Como tal, apenas a variação no tratamento proveniente do instrumento é usada para explicar a variação no resultado. Isto então resolve o viés de auto-seleção. No caso de um instrumento binário (de dois valores), as estimativas de Wald e 2SLS serão idênticas (ver , por exemplo). No entanto, a dificuldade não está na implementação de tal estimativa 2SLS, todos os pacotes estatísticos podem calcular estimativas IV, mas em (a) encontrar um instrumento válido e (b) interpretar os resultados. A discussão irá agora focar estes dois pontos.