Wave Speed on a String under Tension
Para ver como a velocidade de uma onda em uma corda depende da tensão e da densidade linear, considere um pulso enviado por uma corda esticada (Figura \PageIndex{1}}). Quando a corda esticada está em repouso na posição de equilíbrio, a tensão na corda \(F_T) é constante. Considere um pequeno elemento da corda com uma massa igual a (Delta m = Delta x). O elemento de massa está em repouso e em equilíbrio e a força de tensão de cada lado do elemento de massa é igual e oposta.
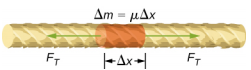
Se você depena uma corda sob tensão, uma onda transversal se move no sentido positivo x, como mostrado na Figura {2}(PageIndex{2}). O elemento de massa é pequeno, mas é aumentado na figura para torná-lo visível. O elemento de massa pequeno oscila perpendicularmente ao movimento da onda como resultado da força de restauração proporcionada pela corda e não se move no sentido x. A tensão FT na corda, que age no sentido positivo e negativo x, é aproximadamente constante e é independente da posição e tempo.
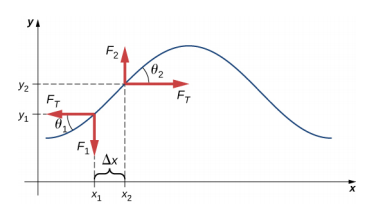
Assumir que a inclinação da corda deslocada em relação ao eixo horizontal é pequena. A força líquida sobre o elemento da corda, agindo paralelamente à corda, é a soma da tensão na corda e da força de restauração. Os componentes x da força de tensão são cancelados, portanto a força da rede é igual à soma dos componentes y da força. A magnitude do componente x da força é igual à força horizontal de tensão da corda, como mostrado na Figura 2. Para obter os componentes y da força, note que o bronzeado (F_F_{1} = -frac{F_{1}}{F_{T}}) e o bronzeado (F_Tan_{2} = Frac{F_{2}}). O {\i1}(tan {\i}theta} é igual à inclinação de uma função em um ponto, que é igual à derivada parcial de y em relação a x nesse ponto. Portanto, {F_F_{1}{F_{T}}) é igual à inclinação negativa da string em x1 e {F_F_{2}{F_{T}} é igual à inclinação da string em x2:
A força da rede está no pequeno elemento de massa pode ser escrita como
\\ldotp]
Utilizando a segunda lei de Newton, a força da rede é igual à massa vezes a aceleração. A densidade linear da corda µ é a massa por comprimento da corda, e a massa da porção da corda é {mu {delta})x,
= Delta ma = Delta x esquerda (frac{\i}{2} y}{\i1}{\i1}parcialmente t^{\i}{\i1}direita) ldotp]
p>Dividindo por FT(delta)x e tomando o limite como se aproxima de zero,
\i}{\i1}{Delta x} & = \frac{\i}{F_{T}}{F_{T}} \Parcialmente parcial… \\ Parcialmente parcial… & = \frac{\mu}{F_{T}}} \Parcialmente parcial… \ldotp {split}]
Recall that the linear wave equation is
/p>
P>Então,
p>>P>P>Solving for \\(v\), vemos que a velocidade da onda em uma corda depende da tensão e da densidade linear
velocidade de uma onda em uma corda sob tensão
A velocidade de um pulso ou onda em uma corda sob tensão pode ser encontrada com a equação
p> onde \(F_T\) é a tensão na corda e \(µ\) é a massa por comprimento da corda.
Exemplo 16.5: A Velocidade de Onda de uma Mola de Guitarra
Numa guitarra de seis cordas, a corda E alta tem uma densidade linear de \(\u_{alto; E}}) = 3.09 x 10-4 kg/m e a corda E baixa tem uma densidade linear de \u_{baixo; E}) = 5.78 x 10-3 kg/m. (a) Se a corda E alta é depenada, produzindo uma onda na corda, qual é a velocidade da onda se a tensão da corda é 56,40 N? (b) A densidade linear da corda de E baixa é aproximadamente 20 vezes maior que a da corda de E alta. Para que as ondas viajem através da corda de E baixo à mesma velocidade da corda de E alto, a tensão precisaria ser maior ou menor que a da corda de E alto? Qual seria a tensão aproximada? (c) Calcular a tensão da corda de E baixa necessária para a mesma velocidade de onda.
Estratégia
- A velocidade da onda pode ser encontrada a partir da densidade linear e da tensão \(v = \sqrt{\frac{F_{T}}{\mu}}.
- Da equação v = {sqrt{\frac{F_{T}}{mu}}, se a densidade linear for aumentada por um fator de quase 20, a tensão precisaria ser aumentada por um fator de 20.
- Sabendo a velocidade e a densidade linear, a equação da velocidade pode ser resolvida para a força da tensão FT = {\mu)v2.
Solução
- Utiliza a equação da velocidade para encontrar a velocidade: $$v = {\frac{F_{\T}}{\mu} = \sqrt{\frac{\frac{56.40\; N}{3.09 {3.09 } vezes 10^{-4}; kg/m}} = 427.23\; m/s {ldotp$$$
- A tensão precisaria ser aumentada por um fator de aproximadamente 20. A tensão seria ligeiramente inferior a 1128 N.
- Utiliza a equação da velocidade para encontrar a tensão real: $$F_{T} = \mu v^{2} = (5.78 ^{-3}} vezes 10^{-3}; kg/m)(427.23\; m/s)^{2} = 1055.00\; N \ldotp$$$
- Esta solução está dentro de 7% da aproximação.
Significado
As notas padrão das seis cordas (E, B, G, D, A, E baixo) são afinadas para vibrar nas frequências fundamentais (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz e 82,41 Hz) quando depenadas. As freqüências dependem da velocidade das ondas na corda e do comprimento de onda das ondas. As seis cordas têm densidades lineares diferentes e são “afinadas” pela mudança das tensões nas cordas. Veremos em Interferência de Ondas que o comprimento de onda depende do comprimento das cordas e das condições de contorno. Para tocar notas diferentes das notas fundamentais, os comprimentos das cordas são alterados pressionando as cordas.
Exercício 16.5
A velocidade de onda de uma onda sobre uma corda depende da tensão e da densidade de massa linear. Se a tensão for duplicada, o que acontece à velocidade das ondas na corda?