Rychlost vlnění na napnuté struně
Abychom zjistili, jak rychlost vlnění na struně závisí na napětí a lineární hustotě, uvažujme impuls vyslaný po napnuté struně (obrázek \(\PageIndex{1}\)). Když je napnutá struna v klidu v rovnovážné poloze, je napětí ve struně \(F_T\) konstantní. Uvažujme malý prvek struny s hmotností rovnou \(\Delta m = \mu \Delta x\). Hmotný prvek je v klidu a v rovnováze a síla napětí na obou stranách hmotného prvku je stejná a opačná.
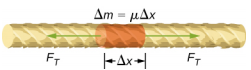
Pokud strunu pod napětím přetáhneme, pohybuje se příčná vlna v kladném směru x, jak ukazuje obrázek \(\PageIndex{2}\). Hmotnostní prvek je malý, ale na obrázku je zvětšen, aby byl vidět. Malý hmotný prvek kmitá kolmo na vlnový pohyb v důsledku působení vratné síly, kterou poskytuje struna, a nepohybuje se ve směru x. Napětí FT v provázku, které působí v kladném a záporném směru x, je přibližně konstantní a nezávisí na poloze a čase.
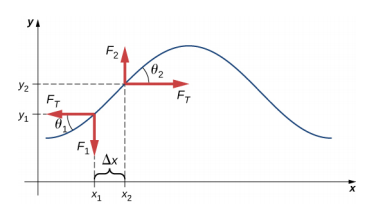
Předpokládejte, že sklon posunuté struny vzhledem k vodorovné ose je malý. Čistá síla působící na prvek struny, která je s ní rovnoběžná, je součtem napětí ve struně a obnovovací síly. Složky x síly tahu se ruší, takže čistá síla je rovna součtu složek y síly. Velikost x-složky síly je rovna vodorovné síle tahu struny \(F_T\), jak je znázorněno na obrázku \(\PageIndex{2}\). Složky síly y získáme tak, že tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}) a \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}). \(\tan \theta\) se rovná sklonu funkce v bodě, který je roven parciální derivaci y vzhledem k x v tomto bodě. Proto se \(\frac{F_{1}}{F_{T}}\) rovná zápornému sklonu struny v bodě x1 a \(\frac{F_{2}}{F_{T}}) se rovná sklonu struny v bodě x2:
\
Čistou sílu působící na malý hmotný prvek lze zapsat jako
\ \ldotp\]
Podle druhého Newtonova zákona je čistá síla rovna hmotnosti krát zrychlení. Lineární hustota struny µ je hmotnost na délku struny a hmotnost části struny je \(\mu \Delta\)x,
\ = \Delta ma = \mu \Delta x \left(\frac{\část^{2} y}{\část t^{2}}\right) \ldotp\]
Dělíme FT\(\Delta\)x a bereme limitu, jak se \(\Delta\)x blíží nule,
\}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\část^{2} y}{\část t^{2}} \\\ \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]
Připomeňme, že lineární vlnová rovnice je
\
Tedy,
\
Řešení pro \(v\), vidíme, že rychlost vlnění na struně závisí na napětí a lineární hustotě
Rychlost vlnění na struně pod napětím
Rychlost impulsu nebo vlnění na struně pod napětím lze zjistit pomocí rovnice
\
kde \(F_T\) je napětí ve struně a \(µ\) je hmotnost na délku struny.
Příklad 16.5: Rychlost vlnění kytarové pružiny
Na šestistrunné kytaře má struna s vysokým E lineární hustotu \(\mu_{Vysoký\; E}\) = 3,09 x 10-4 kg/m a struna s nízkým E má lineární hustotu \(\mu_{Nízký\; E}\) = 5,78 x 10-3 kg/m. (a) Pokud je struna s vysokým E napnuta a vznikne na ní vlna, jaká je rychlost této vlny, je-li napětí struny 56,40 N? (b) Lineární hustota struny s nízkým E je přibližně 20krát větší než hustota struny s vysokým E. Jaká je lineární hustota struny s nízkým E? Aby se vlny šířily strunou s nízkou hustotou E stejnou rychlostí jako strunou s vysokou hustotou E, muselo by být napětí struny větší nebo menší než u struny s vysokou hustotou E? Jaké by bylo přibližné napětí? (c) Vypočítejte napětí struny nízké E potřebné pro stejnou rychlost vlnění.
Strategie
- Rychlost vlnění lze zjistit z lineární hustoty a napětí \(v = \sqrt{\frac{F_{T}}{\mu}}).
- Z rovnice v = \(\sqrt{\frac{F_{T}}{\mu}}\) vyplývá, že pokud se lineární hustota zvýší téměř 20krát, bude třeba zvýšit napětí 20krát.
- Známe-li rychlost a lineární hustotu, můžeme rovnici rychlosti vyřešit pro sílu tahu FT = \(\mu\)v2.
Řešení
- Pomocí rychlostní rovnice zjistíme rychlost: $$v = \sqrt{\frac{F_{T}}{\mu}} = \sqrt{\frac{56.40\; N}{3,09 \krát 10^{-4}\; kg/m}} = 427,23\; m/s \ldotp$
- Napětí bude třeba zvýšit přibližně 20krát. Napětí by bylo o něco menší než 1128 N.
- Pomocí rychlostní rovnice zjistíme skutečné napětí: $$F_{T} = \mu v^{2} = (5,78 \krát 10^{-3}\; kg/m)(427,23\; m/s)^{2} = 1055,00\; N \ldotp$$
- Toto řešení je v rozsahu 7 % aproximace.
Význam
Standardní tóny šesti strun (vysoké E, B, G, D, A, nízké E) jsou naladěny tak, aby při vybrnkávání kmitaly na základních frekvencích (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz a 82,41 Hz). Frekvence závisí na rychlosti vlnění na struně a na vlnové délce vln. Šest strun má různou lineární hustotu a „ladí“ se změnou napětí ve strunách. V kapitole Interference vln uvidíme, že vlnová délka závisí na délce strun a na okrajových podmínkách. Chceme-li zahrát jiné než základní tóny, měníme délky strun tak, že na struny zatlačíme.
Cvičení 16.5
Rychlost vlnění na struně závisí na napětí a lineární hustotě hmoty. Pokud se napětí zdvojnásobí, co se stane s rychlostí vlnění na struně?