Lernziele
Am Ende dieses Abschnitts werden Sie in der Lage sein:
- Die zeitlich gemittelte Energiedichte elektromagnetischer Wellen in Form ihrer elektrischen und magnetischen Feldamplituden ausdrücken
- Berechnen Sie den Poynting-Vektor und die Energieintensität elektromagnetischer Wellen
- Erläutern Sie, wie die Energie einer elektromagnetischen Welle von ihrer Amplitude abhängt, während die Energie eines Photons proportional zu seiner Frequenz ist
Jeder, der schon einmal einen Mikrowellenherd benutzt hat, weiß, dass elektromagnetische Wellen Energie enthalten. Manchmal ist diese Energie offensichtlich, wie zum Beispiel in der Wärme der Sommersonne. Manchmal ist sie subtil, wie die nicht spürbare Energie von Gammastrahlen, die lebende Zellen zerstören können.
Elektromagnetische Wellen bringen durch ihre elektrischen und magnetischen Felder Energie in ein System ein. Diese Felder können Kräfte ausüben und Ladungen im System bewegen und somit Arbeit an ihnen verrichten. Eine elektromagnetische Welle selbst enthält jedoch Energie, unabhängig davon, ob sie absorbiert wird oder nicht. Einmal erzeugt, transportieren die Felder Energie von einer Quelle weg. Wenn später etwas Energie absorbiert wird, verringern sich die Feldstärken, und alles, was übrig bleibt, wandert weiter.
Je größer die Stärke der elektrischen und magnetischen Felder ist, desto mehr Arbeit können sie verrichten, und desto größer ist die Energie, die die elektromagnetische Welle trägt. Bei elektromagnetischen Wellen ist die Amplitude die maximale Feldstärke der elektrischen und magnetischen Felder (Abbildung \(\PageIndex{1}\)). Die Wellenenergie wird durch die Wellenamplitude bestimmt.
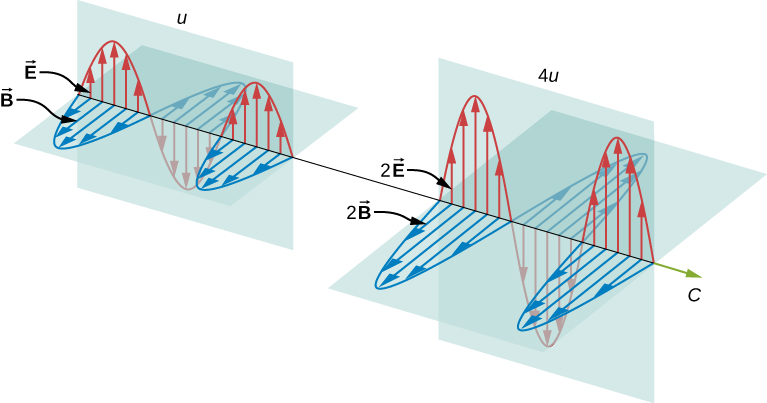
Für eine ebene Welle, die sich in Richtung der positiven x-Achse ausbreitet, wobei die Phase der Welle so gewählt ist, dass das Wellenmaximum im Ursprung bei \(t = 0\) liegt, gehorchen die elektrischen und magnetischen Felder den Gleichungen
Die Energie in jedem Teil der elektromagnetischen Welle ist die Summe der Energien der elektrischen und magnetischen Felder. Diese Energie pro Volumeneinheit, oder Energiedichte u, ist die Summe der Energiedichte des elektrischen Feldes und der Energiedichte des magnetischen Feldes. Die Ausdrücke für beide Feldenergiedichten wurden bereits erörtert (\(u_E\) bei der Kapazität und \(u_B\) bei der Induktivität). Kombiniert man diese Beiträge, so erhält man
Der Ausdruck \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}B\) zeigt dann, dass die magnetische Energiedichte \(u_B\) und die elektrische Energiedichte \(u_E\) gleich sind, obwohl wechselnde elektrische Felder im Allgemeinen nur kleine Magnetfelder erzeugen. Die Gleichheit der elektrischen und magnetischen Energiedichte führt zu
Die Energiedichte bewegt sich mit den elektrischen und magnetischen Feldern in ähnlicher Weise wie die Wellen selbst.
Wir können die Transportrate der Energie finden, indem wir ein kleines Zeitintervall \(\Delta t\) betrachten. Wie in Abbildung \(\PageIndex{2}\) gezeigt, durchläuft die in einem Zylinder der Länge \(c\Delta t\) und der Querschnittsfläche A enthaltene Energie die Querschnittsebene im Intervall \(\Delta t\).
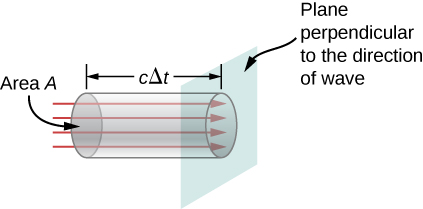
Die Energie, die die Fläche \(A\) in der Zeit \(\Delta t\) durchläuft, ist
Die Energie pro Flächeneinheit pro Zeiteinheit, die eine Ebene senkrecht zur Welle durchläuft, die als Energiefluss bezeichnet und mit \(S\) bezeichnet wird, kann berechnet werden, indem die Energie durch die Fläche \(A\) und das Zeitintervall \(\Delta t\) geteilt wird.
Allerdings hängt der Energiefluss durch eine beliebige Fläche auch von der Ausrichtung der Fläche ab. Um die Richtung zu berücksichtigen, führen wir einen Vektor \(\vec{S}\), den sogenannten Poynting-Vektor, mit folgender Definition ein:
Das Kreuzprodukt von \(\vec{E}\) und \(\vec{B}\) zeigt in die Richtung, die senkrecht zu beiden Vektoren steht. Um zu bestätigen, dass die Richtung von \(\vec{S}\) diejenige der Wellenausbreitung ist, und nicht deren Negativ, kehren Sie zu Abbildung 16.3.2 zurück. Beachten Sie, dass die Lenz’schen und Faraday’schen Gesetze besagen, dass bei einem zeitlich zunehmenden Magnetfeld das elektrische Feld bei \(x\) größer ist als bei \(x + \Delta x\). Das elektrische Feld nimmt mit zunehmendem \(x\) zum gegebenen Zeitpunkt und Ort ab. Die Proportionalität zwischen elektrischem und magnetischem Feld setzt voraus, dass das elektrische Feld mit der Zeit zusammen mit dem magnetischen Feld zunimmt. Dies ist nur möglich, wenn sich die Welle im Diagramm nach rechts ausbreitet. In diesem Fall zeigen die relativen Orientierungen, dass \(\vec{S} = \frac{1}{\mu_0} \vec{E} \mal \vec{B}\) genau in der Ausbreitungsrichtung der elektromagnetischen Welle liegt.
Der Energiestrom an einem beliebigen Ort variiert auch in der Zeit, wie man sieht, wenn man \(u\) aus Gleichung 16.3.19 in Gleichung \ref{16.27} einsetzt.
Da die Frequenz des sichtbaren Lichts sehr hoch ist, in der Größenordnung von \(10^{14} \, Hz\), ist der Energiestrom für sichtbares Licht durch ein beliebiges Gebiet eine extrem schnell variierende Größe. Die meisten Messgeräte, einschließlich unserer Augen, erfassen nur einen Mittelwert über viele Zyklen. Der zeitliche Mittelwert des Energieflusses ist die Intensität \(I\) der elektromagnetischen Welle und ist die Leistung pro Flächeneinheit. Sie lässt sich durch die Mittelung der Kosinusfunktion in Gleichung \ref{16.29} über einen vollständigen Zyklus ausgedrückt werden, was dem Zeitmittelwert über viele Zyklen entspricht (hier ist \(T\) eine Periode):
Wir können entweder das Integral auswerten oder aber feststellen, dass, da sich Sinus und Kosinus nur in der Phase unterscheiden, der Durchschnitt über einen vollständigen Zyklus für \(cos^2 \, (\xi)\) derselbe ist wie für \(sin^2 \, (\xi)\), um
= \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
wobei die spitzen Klammern \(\langle . . . \rangle \) für die Zeitmittelung stehen. Die Intensität von Licht, das sich mit der Geschwindigkeit \(c\) im Vakuum bewegt, ist dann
in Bezug auf die maximale elektrische Feldstärke \(E_0\), die auch die elektrische Feldamplitude ist. Durch algebraische Manipulation ergibt sich die Beziehung
wobei \(B_0\) die magnetische Feldamplitude ist, die mit der maximalen magnetischen Feldstärke identisch ist. Ein weiterer Ausdruck für \(I_{avg}\) in Bezug auf die elektrischen und magnetischen Feldstärken ist nützlich. Setzt man die Tatsache ein, dass \(cB_0 = E_0\) ist, wird der vorherige Ausdruck zu
Wir können diejenige der drei vorangegangenen Gleichungen verwenden, die uns am meisten zusagt, denn die drei Gleichungen sind eigentlich nur verschiedene Versionen desselben Ergebnisses: Die Energie einer Welle hängt mit der Amplitude im Quadrat zusammen. Da diese Gleichungen auf der Annahme beruhen, dass die elektromagnetischen Wellen sinusförmig sind, ist die Spitzenintensität doppelt so hoch wie die durchschnittliche Intensität, d.h. \(I_0 = 2I\).
Beispiel \(\PageIndex{1}\): Ein Laserstrahl
Der Strahl eines kleinen Laborlasers hat typischerweise eine Intensität von etwa \(1,0 \times 10^{-3} W/m^2\). Berechnen Sie unter der Annahme, dass der Strahl aus ebenen Wellen besteht, die Amplituden der elektrischen und magnetischen Felder im Strahl.
Strategie
Benutzen Sie die Gleichung, die die Intensität als elektrisches Feld ausdrückt, um das elektrische Feld aus der Intensität zu berechnen.
Lösung
Aus Gleichung \ref{16.31} ist die Intensität des Laserstrahls
Die Amplitude des elektrischen Feldes ist also
&= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\ &= 0,87 \, V/m. \end{align*}\]
Die Amplitude des Magnetfeldes ergibt sich aus:
\
Glühbirnenfelder
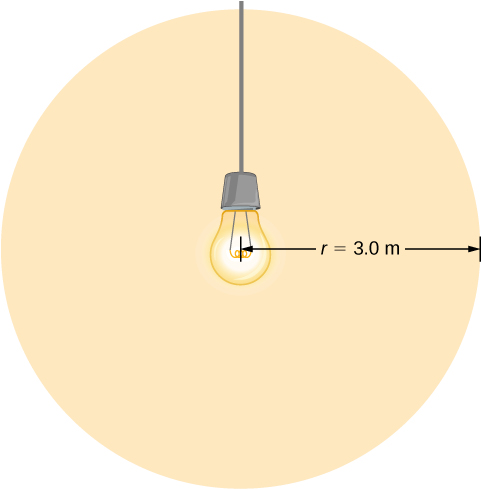
Eine Glühbirne strahlt 5,00 W Leistung als sichtbares Licht ab. Wie groß sind die mittleren elektrischen und magnetischen Felder des Lichts in 3,0 m Entfernung?
Strategie
Angenommen, die Leistung P der Glühbirne ist gleichmäßig über eine Kugel mit dem Radius 3,0 m verteilt, so kann man die Intensität und daraus das elektrische Feld berechnen.
Lösung
Die als sichtbares Licht abgestrahlte Leistung ist dann
(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},\)
(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Bedeutung
Die Intensität I fällt mit dem Abstand zum Quadrat ab, wenn die Strahlung gleichmäßig in alle Richtungen gestreut wird.
Funkreichweite
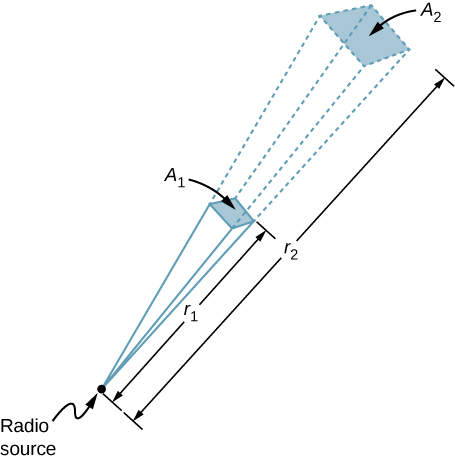
Ein 60-kW-Funksender auf der Erde sendet sein Signal an einen 100 km entfernten Satelliten (Abbildung \(\PageIndex{3}\)). In welcher Entfernung in der gleichen Richtung hätte das Signal die gleiche maximale Feldstärke, wenn die Ausgangsleistung des Senders auf 90 kW erhöht würde?
Strategie
Die Fläche, über die sich die Leistung in einer bestimmten Richtung ausbreitet, nimmt mit dem Quadrat der Entfernung zu, wie in Abbildung \(\PageIndex{3}\) dargestellt. Ändern Sie die Ausgangsleistung P um den Faktor (90 kW/60 kW) und ändern Sie die Fläche um denselben Faktor, damit \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) gleich bleibt. Benutze dann das Verhältnis der Fläche A im Diagramm zum Quadrat der Strecke, um die Strecke zu finden, die die berechnete Flächenänderung bewirkt.
Lösung
Wenn man die Proportionalität der Flächen zu den Quadraten der Entfernungen verwendet und löst, erhält man aus dem Diagramm
r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \\ &= 122 \, km. \end{align*}\]
Bedeutung
Die Reichweite eines Funksignals ist die maximale Entfernung zwischen Sender und Empfänger, die einen normalen Betrieb ermöglicht. Ohne Komplikationen wie Reflexionen an Hindernissen folgt die Intensität dem Gesetz des umgekehrten Quadrats, und eine Verdoppelung der Reichweite würde eine Vervierfachung der Leistung erfordern.
Beitragende und Namensnennung
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen beitragenden Autoren. Dieses Werk wird von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0) lizenziert.