Objectivos de Aprendizagem
Ao final desta secção, você será capaz de:
- Expressar a densidade de energia das ondas electromagnéticas em termos de amplitude do campo eléctrico e magnético
- Calcular o vector Poynting e a intensidade energética das ondas electromagnéticas
- Explicar como a energia de uma onda electromagnética depende da sua amplitude, enquanto que a energia de um fotão é proporcional à sua frequência
Ainda que tenha utilizado um forno de microondas sabe que há energia nas ondas electromagnéticas. Às vezes essa energia é óbvia, como no calor do sol de verão. Outras vezes, é sutil, como a energia não sentida dos raios gama, que pode destruir células vivas.
Ondas electromagnéticas trazem energia para um sistema em virtude dos seus campos eléctricos e magnéticos. Esses campos podem exercer forças e mover cargas no sistema e, assim, trabalhar neles. Entretanto, há energia em uma onda eletromagnética em si, seja ela absorvida ou não. Uma vez criados, os campos transportam energia para longe de uma fonte. Se alguma energia é absorvida mais tarde, as forças do campo são diminuídas e tudo o que resta viaja em.
Claramente, quanto maior a força dos campos eléctricos e magnéticos, mais trabalho podem fazer e maior a energia que a onda electromagnética transporta. Nas ondas eletromagnéticas, a amplitude é a força máxima dos campos elétricos e magnéticos (Figura 1). A energia da onda é determinada pela amplitude da onda.
Para uma onda plana que viaja na direcção do eixo x positivo com a fase da onda escolhida de modo a que o máximo da onda esteja na origem em \(t = 0\), os campos eléctricos e magnéticos obedecem às equações
\
\
A energia em qualquer parte da onda electromagnética é a soma das energias dos campos eléctricos e magnéticos. Esta energia por unidade de volume, ou densidade de energia u, é a soma da densidade da energia do campo eléctrico e da densidade da energia do campo magnético. Expressões para ambas as densidades de energia do campo foram discutidas anteriormente (u_E) em Capacitância e (u_B) em Indutância). Combinando estas contribuições, obtemos
p>p> A expressão \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}B}) mostra então que a densidade de energia magnética \(u_B) e a densidade de energia eléctrica \(u_E) são iguais, apesar do facto de os campos eléctricos em mudança produzirem geralmente apenas pequenos campos magnéticos. A igualdade das densidades de energia eléctrica e magnética leva a
p>
A densidade de energia move-se com os campos eléctricos e magnéticos de forma semelhante às próprias ondas.
Podemos encontrar a taxa de transporte de energia considerando um pequeno intervalo de tempo {\i}. Como mostra a Figura 2, a energia contida em um cilindro de comprimento (delta t) e seção transversal A passa pelo plano da seção transversal no intervalo (delta t).
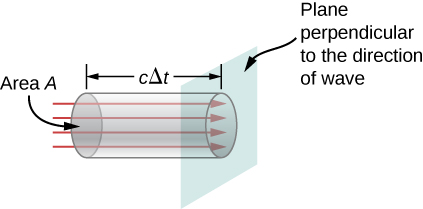
A energia que passa pela área (A) no tempo é
p>>p>p> A energia por unidade de área por unidade de tempo que passa por um plano perpendicular à onda, chamado fluxo de energia e denotado por S, pode ser calculado dividindo a energia pela área e pelo intervalo de tempo.
\\
Mais geralmente, o fluxo de energia através de qualquer superfície também depende da orientação da superfície. Para levar em conta a direção, introduzimos um vetor chamado vetor Poynting, com a seguinte definição:
O produto cruzado dos vetores {E} e {B} aponta na direção perpendicular a ambos os vetores. Para confirmar que a direção da propagação da onda, e não sua direção negativa, retorna à Figura 16.3.2. Note que as leis de Lenz e Faraday implicam que quando o campo magnético mostrado está aumentando no tempo, o campo elétrico é maior em x (x) do que em x (x + Delta x). O campo elétrico está diminuindo com o aumento no tempo e localização determinados. A proporcionalidade entre campos elétricos e magnéticos exige que o campo elétrico aumente no tempo junto com o campo magnético. Isto só é possível se a onda estiver a propagar-se para a direita no diagrama, caso em que, as orientações relativas mostram que a propagação da onda electromagnética é especificamente na direcção da propagação da onda electromagnética.O fluxo de energia em qualquer lugar também varia no tempo, como pode ser visto pela substituição da Equação 16.3.19 pela Equação 16.27. A maioria dos aparelhos de medição, incluindo os nossos olhos, detecta apenas uma média ao longo de muitos ciclos. A média temporal do fluxo de energia é a intensidade da onda electromagnética e é a potência por unidade de área. Ela pode ser expressa através da média da função co-seno na Equação {16}ref.29} ao longo de um ciclo completo, que é o mesmo que a média de tempo ao longo de muitos ciclos (aqui, T) é um período):Podemos avaliar a integral, ou então notar que como o seno e o cosseno diferem apenas em fase, a média ao longo de um ciclo completo para \\i(cos^2, (\xi)}) é a mesma que para \i(sin^2, (\i)}), para obter
= \i(2) \1 {2}{2}.{2}.{2}P>>onde os parênteses angulares {3}({3}ângulo . . . . . .{4}) representam a operação de economia de tempo. A intensidade da luz movendo-se em velocidade no vácuo é então encontrada
em termos da intensidade máxima do campo elétrico { E_0}, que é também a amplitude do campo elétrico. A manipulação algébrica produz a relação
\\
onde \(B_0\) é a amplitude do campo magnético, que é a mesma que a intensidade máxima do campo magnético. Mais uma expressão para { I_{avg}) em termos de intensidade do campo eléctrico e magnético é útil. Substituindo o fato de que \(cB_0 = E_0\), a expressão anterior torna-se
\
Podemos usar a que for mais conveniente das três equações anteriores, porque as três equações são realmente apenas versões diferentes do mesmo resultado: A energia de uma onda está relacionada com a amplitude ao quadrado. Além disso, como estas equações são baseadas no pressuposto de que as ondas electromagnéticas são sinusoidais, a intensidade de pico é o dobro da intensidade média; ou seja, \\i(I_0 = 2I\i).
Exemplo \i(PageIndex{1}}): Um raio laser
O raio de um pequeno laser de laboratório normalmente tem uma intensidade de cerca de ^(1.0 ^^ vezes 10^{-3} W/m^2^). Assumindo que o feixe é composto por ondas planas, calcule as amplitudes dos campos eléctrico e magnético no feixe.
Estratégia
Utilize a equação que expressa a intensidade em termos de campo eléctrico para calcular o campo eléctrico a partir da intensidade.
Solução
Da equação \ref{16.31}, a intensidade do feixe laser é
\
A amplitude do campo eléctrico é portanto
\ &= \sqrt{\frac{2}{(3.00 vezes 10^8 m/s)(8.85 vezes 10^{-12} F/m)}esquerda(1.0 ^^ vezes 10^{-3} W/m^2 ^direita)} &= 0.87, V/m. \A amplitude do campo magnético pode ser obtida a partir de:
/p>
Campos de Lâmpadas
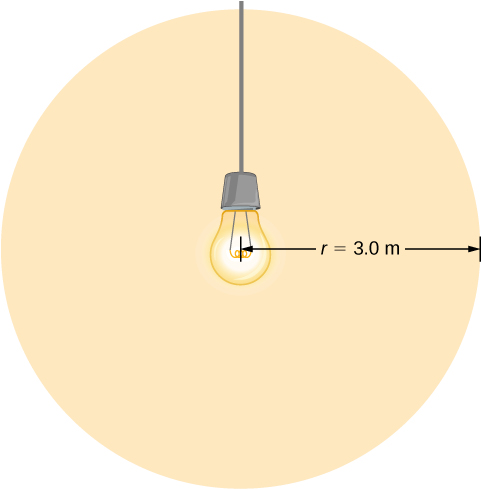
Uma lâmpada emite 5,00 W de potência como luz visível. Quais são os campos eléctricos e magnéticos médios da luz a uma distância de 3,0 m?
Estratégia
P>Conteça que a potência da lâmpada P é distribuída uniformemente por uma esfera de raio 3,0 m para calcular a intensidade, e a partir dela, o campo eléctrico.
Solução
A energia irradiada como luz visível é então
(I = \frac{P}{4\pi r^2} = \frac{c\psilon_0 E_0^2}{2},\P>P>P>(E_0 = ^2frac{P}{4\pi r^2 c^2 c^epsilon_0}} = ^2frac{5.00, W}{4\pi (3.0, m)^2 (3.00 vezes 10^8, m/s)(8.85 vezes 10^{-12} C^2/N ^cdot m^2)} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \ vezes 10^{-8}, T\).
Significado
A intensidade cai como a distância ao quadrado se a radiação estiver dispersa uniformemente em todas as direcções.
Alcance do rádio
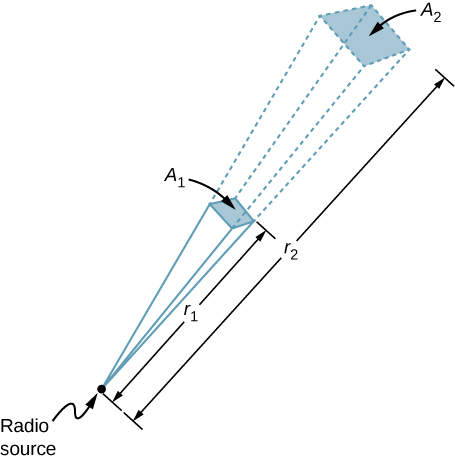
Um rádio transmissor de 60-kW na Terra envia o seu sinal para um satélite a 100 km de distância (Figura \PageIndex{3}). A que distância na mesma direção o sinal teria a mesma intensidade máxima de campo se a potência de saída do transmissor fosse aumentada para 90 kW?
Strategy
A área sobre a qual a potência em uma determinada direção é dispersa aumenta conforme a distância ao quadrado, como ilustrado na Figura \PageIndex{3}. Mude a potência de saída P por um fator de (90 kW/60 kW) e mude a área pelo mesmo fator para manter \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}}} o mesmo. Em seguida, use a proporção da área A no diagrama para distância ao quadrado para encontrar a distância que produz a mudança calculada na área.
Solução
Usando a proporcionalidade das áreas aos quadrados das distâncias, e resolvendo, obtemos do diagrama
\ r_2 &= \sqrt{\frac{90}{60}}(100 \, km) {&
= 122 \, km. \end{align*}]
Significance
O alcance de um sinal de rádio é a distância máxima entre o transmissor e o receptor que permite uma operação normal. Na ausência de complicações como reflexos de obstáculos, a intensidade segue uma lei quadrada inversa, e duplicar o alcance exigiria multiplicar a potência por quatro.
Contribuidores e Atribuições
- p>Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs com muitos autores contribuintes. Esta obra é licenciada pela OpenStax University Physics sob uma Creative Commons Attribution License (por 4.0).